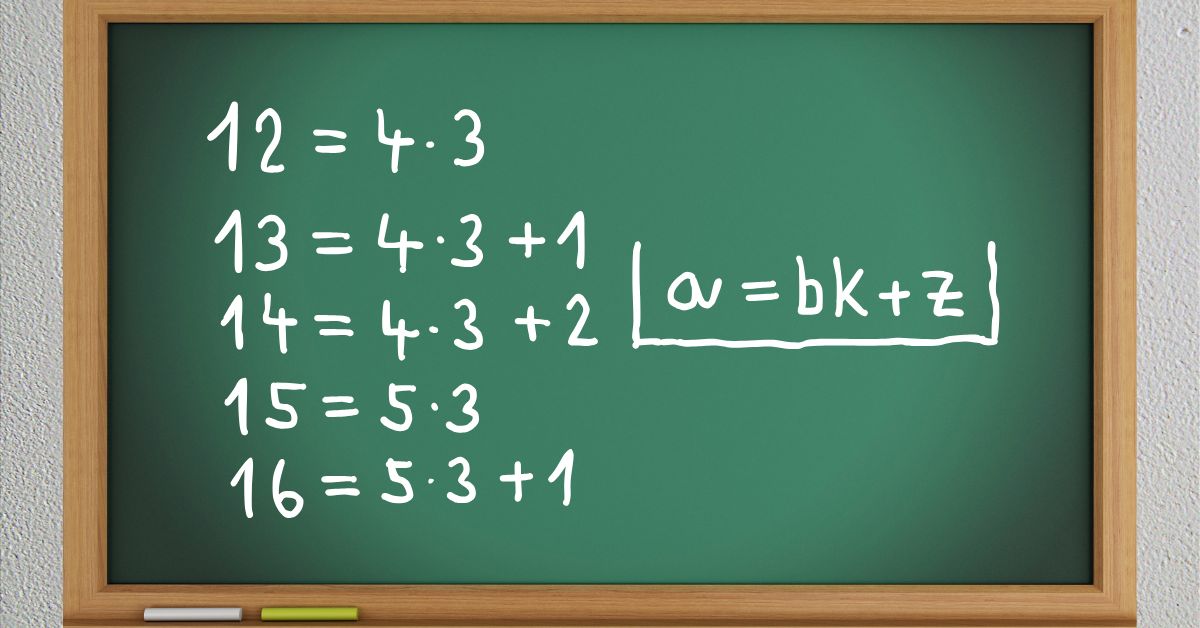Zbytkové tvary přirozených čísel

V předchozím článku jsme si probrali rozvinutý zápis přirozených čísel, násobek a dělitel.

V tomto článku navážeme ještě jiným druhem zápisu přirozených čísel, kterému se říká zbytkový tvar a zabrousíme trochu více do abstraktní oblasti, abychom si procvičili právě naše abstraktní myšlení.

Vysvětleme si na příkladech, o co jde.

Budeme si postupně volit přirozená čísla b, které jsou větší než 1, jak to definice vyžaduje. Začneme u čísla b = 2. Nyní můžeme každé přirozené číslo n vyjádřit tak, že ho vydělíme dvěma a napíšeme ho jako násobek čísla 2 plus zbytek po dělení.

Pro b = 2 můžeme vyjádřit například čísla od 1 do 9 tímto způsobem:

$ 1 = 2 \cdot 0 + 1 $
$ 2 = 2 \cdot 1 $
$ 3 = 2 \cdot 1 + 1 $
$ 4 = 2 \cdot 2 $
$ 5 = 2 \cdot 2 + 1 $
$ 6 = 2 \cdot 3 $
$ 7 = 2 \cdot 3 + 1 $
$ 8 = 2 \cdot 4 $
$ 9 = 2 \cdot 4 + 1 $

Zkrátka napíšeme, kolikrát musíme vynásobit číslo 2 a jaký musíme přičíst zbytek (pokud vůbec nějaký), abychom obdrželi číslo, které takto vyjadřujeme. A právě tento zápis se nazývá zbytkový tvar přirozeného čísla.

Nyní si zvolme b = 3 a opět pro něj vyjádřeme čísla od 1 do 10:

$ 1 = 3 \cdot 0 + 1 $
$ 2 = 3 \cdot 0 + 2$
$ 3 = 3 \cdot 1 $
$ 4 = 3 \cdot 1 + 1 $
$ 5 = 3 \cdot 1 + 2 $
$ 6 = 3 \cdot 2 $
$ 7 = 3 \cdot 2 + 1 $
$ 8 = 3 \cdot 2 + 2 $
$ 9 = 3 \cdot 3 $

A nakonec ještě pro b = 4:

$ 1 = 4 \cdot 0 + 1 $
$ 2 = 4 \cdot 0 + 2$
$ 3 = 4 \cdot 0 + 3 $
$ 4 = 4 \cdot 1 $
$ 5 = 4 \cdot 1 + 1 $
$ 6 = 4 \cdot 1 + 2$
$ 7 = 4 \cdot 1 + 3 $
$ 8 = 4 \cdot 2 $
$ 9 = 4 \cdot 2 + 1 $

Abychom mohli nějaké číslo vyjádřit ve zbytkovém tvaru, musíme mít zadáno, pro jaké číslo b tak máme učinit.

Mohli bychom mít například následující zadání: Vyjádřete číslo 58 ve zbytkovém tvaru pro b = 7. Řešení by vypadalo takto: číslo 58 celočíselně vydělíme číslem 7 – dostaneme 8 a zbytek 2. Výsledek zapíšeme ve tvaru:

$$ 58 = 7 \cdot 8 + 2 $$

Přechod k abstrakci

Nyní se pomalu připravíme na to, k jakým typům úloh se zbytkový tvar přirozených čísel používá.

Z předcházejících úvah vyplývá, že ze dvou za sebou následujících přirozených čísel je právě jedno číslo dělitelné dvěma a to znamená, že součin každých dvou za sebou následujících čísel je dělitelný dvěma. Budeme-li mít např. čísla 11 a 12, tak protože číslo 12 je dělitelné dvěma, bude dělitelný dvěma i součin $ 11 \cdot 12 = 132 $.

V tomto našem příkladu je $ 12 : 2 = 6 $, to znamená, že do čísla 12 se číslo 2 vejde přesně šestkrát. A vynásobíme-li číslo 12 libovolným přirozeným číslem, tak číslo 2 se do takto získaného výsledku vejde tolikrát navíc, kolikrát jsme číslo 12 vynásobili, a tím pádem beze zbytku.

Skutečnost, že součin každých dvou za sebou následujících čísel je dělitelný dvěma, můžeme zapsat takto:

$$ 2 \mid n(n + 1) $$

kde n je libovolné přirozené číslo a (n + 1) je číslo o jedničku větší. To znamená, že čísla n a (n + 1) jsou za sebou následující. Toto n v našem zápisu se násobí s výrazem (n + 1), což nám dá právě zmíněný součin dvou po sobě následujících přirozených čísel. Číslo 2 před znakem ‚|‘ pak znamená, že tento součin je dělitelný dvěma.

Dosadíme-li za n například číslo 11, pak závorka (n + 1) bude reprezentovat číslo $ (11 + 1) = 12 $ a celý výraz n(n + 1) bude součinem těchto čísel, tedy bude platit:

$$ n(n + 1) = 11 \cdot (11 + 1) = 11 \cdot 12 = 132 $$.

A toto číslo je dělitelné dvěma. Dosadíme-li za n jiné číslo, např. 5, potom závorka (n + 1) bude mít hodnotu 6 a celý výraz n(n + 1) bude $ 5 \cdot (5 + 1) = 5 \cdot 6 = 30 $, což je opět číslo dělitelné dvěma.

Obdobně součin každých tří za sebou následujících čísel je dělitelný třemi, protože právě jedno z nich je dělitelné třemi. Tuto skutečnosti zapíšeme jako:

$$ 3 \mid n(n+1)(n+2) $$

Dosadíme-li na n například číslo 4, pak závorka (n + 1) bude reprezentovat číslo $ (4 + 1) = 5 $ a závorka (n + 2) číslo $ (4 + 2) = 6 $. Z těchto tří čísel je třemi dělitelné číslo 6 a tím pádem bude třemi dělitelný i součin $ 4 \cdot 5 \cdot 6 = 120 $.

Součin tří za sebou následujících čísel můžeme zapsat i jinými způsoby, např. jako $ (n \; – \; 1)n(n + 1) $. Opět si představme nějaký konkrétní příklad – jestliže zvolíme n = 10, potom bude $ (n \; – \; 1) = (10 \; – \; 1) = 9 $ a $ (n + 1) = (10 + 1) = 11 $, takže získáme posloupnost tří po sobě následujících přirozených čísel 9, 10 a 11. A protože součin tří za sebou následujících čísel je dělitelný třemi, tak i v tomto případě můžeme napsat:

$$ 3 \mid (n \; – \; 1)n(n + 1) $$

A podobně bychom mohli pokračovat dál: součet každých čtyř za sebou jdoucích přirozených čísel je dělitelný čtyřmi, součet každých pěti za sebou jdoucích přirozených čísel je dělitelný pěti atd.

Ale také například platí, že součet každých tří po sobě jdoucích přirozených čísel je dělitelný šesti, protože minimálně jedno z nich je dělitelné dvěma a právě jedno z nich je dělitelné třemi, což znamená, že tento součin je dělitelný dvěma a třemi zároveň. A číslo, které je dělitelné dvěma a třemi zároveň, je dělitelné šesti.

Důkazové úlohy

Výše zmíněné poznatky se používají v některých důkazových úlohách.

Příklad:

Dokažte, že pro každé přirozené číslo n je $ n^3 \; – \; n $ dělitelné šesti.

Výraz $ n^3 \; – \; n $ upravíme vytknutím n před závorku. Dostaneme $ n(n^2 \; – \; 1) $, výraz v závorce dále rozložíme na součin pomocí vzorce pro rozdíl druhých mocnin, a nakonec si pro lepší přehlednost jednotlivé činitele uspořádáme od nejmenších po největší:

\begin{align*} n^3 \; – \; n &= n(n^2 \; – \; 1) = n(n + 1)(n \; – \; 1)= \\ &= (n \; – \; 1)n(n + 1) \end{align*}

Získali jsme rozdíl tří za sebou následujících přirozených čísel. Alespoň jedno z nich je dělitelné dvěma, právě jedno z nich je dělitelné třemi, a proto je jejich součin dělitelný šesti.

Jiný příklad:

Dokažte, že pro každé přirozené číslo n je $ n^4 \; – \; n^2 $ dělitelné dvanácti.

Z výrazu $ n^4 \; – \; n^2 $ vytkneme $ n^2 $, závorku rozložíme pomocí vzorce pro rozdíl druhých mocnin, a nakonec si jednotlivé činitele uspořádáme od nejmenších po největší:

\begin{align*} n^4 \; – \; n^2 &= n^2(n^2 \; – \; 1) = n^2(n + 1)(n \; – \; 1) \\ &= (n \; – \; 1)n^2(n + 1) \end{align*}

Alespoň jeden činitel je dělitelný třemi a alespoň dva činitelé jsou dělitelné dvěma. Pokud totiž je dělitelné dvěma číslo n, tak protože činitel $ n^2 $ je totéž jako $ n \cdot n $, máme toto n v součinu de facto dvakrát; není-li dělitelné dvěma číslo n, pak jsou dělitelná dvěma čísla (n – 1) a (n + 1). Ať tak či onak, součin dvou čísel, která jsou dělitelná dvěma, je dělitelný čtyřmi. Celý výraz je tedy dělitelný třemi a čtyřmi zároveň, což znamená, že je dělitelný dvanácti.

Závěr

V tomto článku jsme se podívali na zbytkové tvary přirozených čísel, načež jsme si více ponořili do jejich abstraktní oblasti, a nakonec jsme lehce zabrousili do důkazových úloh, které se zbytkovým tvarem souvisí.

V následujícím článku si probereme hodně praktickou a používanou dovednost, kterou představují znaky dělitelnosti.