Vzdálenost bodů

V předchozím článku jsme se věnovali souřadnicím v prostoru.

V tomto článku si ukážeme, jak můžeme spočítat vzdálenost dvou bodů, známe-li jejich souřadnice.

Vzdálenost bodů v rovině

Začneme výpočtem vzdálenosti bodů v rovině, který si ukážeme na příkladu, načež daný postup zobecníme.

Příklad 1

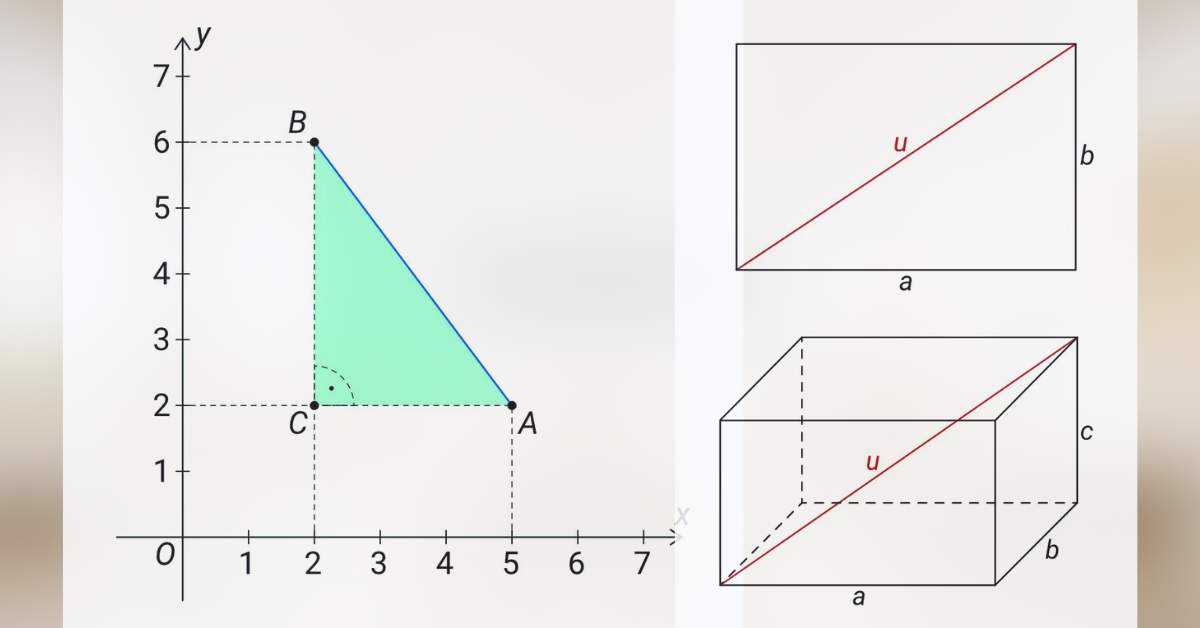
Vypočítejte vzdálenost bodů A[5; 2] a B[2; 6].

Řešení

Podívejte se na následující obrázek:

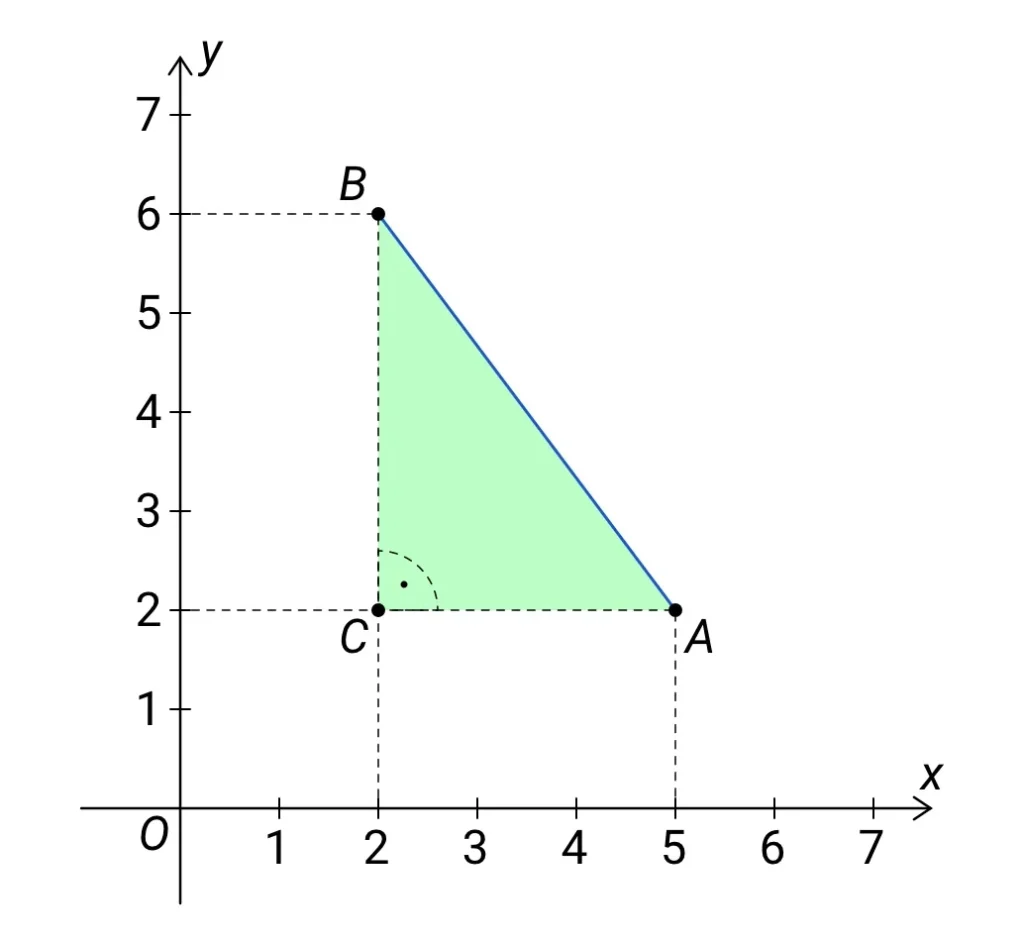
Body A[5; 2] a B[2; 6] jsme doplnili bodem C na pravoúhlý trojúhelník ABC o přeponě AB tak, aby jeho odvěsny AC a BC byly rovnoběžné se souřadnicovými osami. Vzdálenost bodů A a B je současně délkou přepony AB. Proto tuto vzdálenost můžeme vypočítat pomocí Pythagorovy věty.

Délka odvěsny AC je dána rozdílem x-ových souřadnic bodů A a C. Protože x-ová souřadnice bodu C je stejná jako x-ová souřadnice bodu B, můžeme říct, že délka odvěsny AC je dána rozdílem x-ových souřadnic bodů A a B, resp. B a A – na pořadí zde nezáleží.

Obdobně délka odvěsny BC je dána rozdílem y-ových souřadnic bodů B a C. Protože y-ová souřadnice bodu C je stejná jako y-ová souřadnice bodu A, můžeme říct, že délka odvěsny BC je dána rozdílem y-ových souřadnic bodů B a A.

Připomeňme ještě, že x-ové souřadnice značíme s dolním indexem 1 a y-ové souřadnice s dolním indexem 2.

Pro délku odvěsny AC tedy platí:

\[ |AC| = b_1 -a_1 = 2 -5 = -3 \]

Obdobně pro délku odvěsny BC platí:

\[ |BC| = b_2 -a_2 = 6 -2 = 4 \]

U délky odvěsny AC nám vyšlo záporné číslo (-3), přestože je samozřejmě kladná (3), ale to vůbec nevadí, protože toto číslo se ve vzorci odpovídajícímu Pythagorově větě umocní na druhou a $ (-3)^2 $ dá stejný výsledek jako $ 3^2 $, tedy 9.

Z Pythagorovy věty dostaneme:

\[ |AB| = \sqrt{(-3)^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]

V analytické geometrii nepoužíváme žádné jednotky, jako např. centimetry, decimetry, metry apod. Všechny metrické veličiny (vzdálenosti, velikosti atd.) vyjadřujeme pouze číslem.

Nyní můžeme náš postup zobecnit tím, že do vzorce pro Pythagorovu větu dosadíme jako délku jedné odvěsny výraz $ b_1 -a_1 $ a jako délku druhé odvěsny výraz $ b_2 -a_2 $.

Ukažme si ještě jeden příklad:

Příklad 2

Vypočítejte vzdálenost bodů K[8; -2] a L[-4; 3].

Řešení

\begin{align*} |KL| &= \sqrt{(l_1 -k_1)^2 + (l_2 -k_2)^2} = \\ &= \sqrt{(-4 -8)^2 + (3 -(-2))^2} = \\ &= \sqrt{(-12)^2 + 5^2} = \sqrt{144 + 25} = \\ &= \sqrt{169} = 13 \end{align*}

Vzdálenost bodů v prostoru

K výpočtu vzdálenosti bodů v prostoru můžeme použít tzv. zobecněnou Pythagorovu větu.

Pokud v rovině chceme spočítat například délku úhlopříčky u obdélníku se stranami a, b – viz následující obrázek:

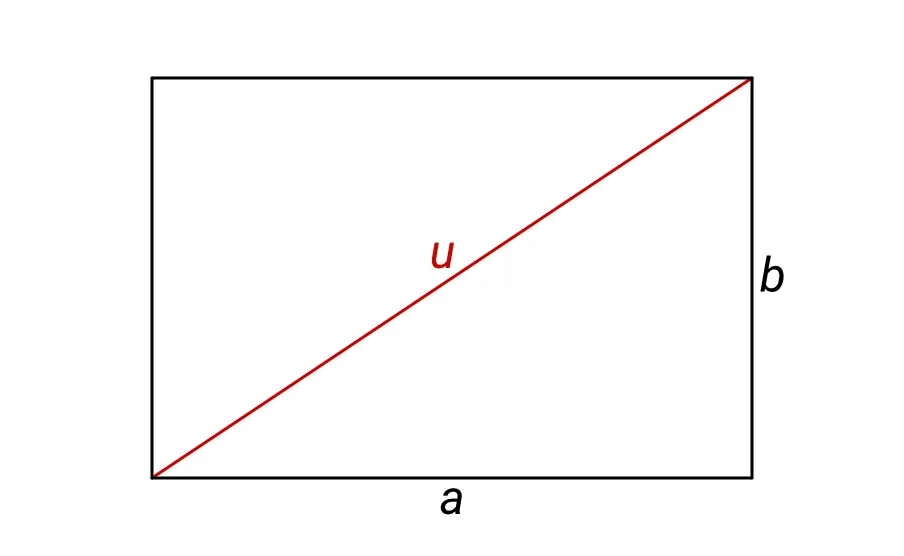
použijeme „běžnou“ Pythagorovu větu, tedy:

$$ u = \sqrt{a^2 + b^2} $$

Obdélník je dvourozměrný útvar. Když jeden rozměr přidáme a půjdeme do prostoru, dostaneme kvádr se stranami a, b, c – viz následující obrázek:

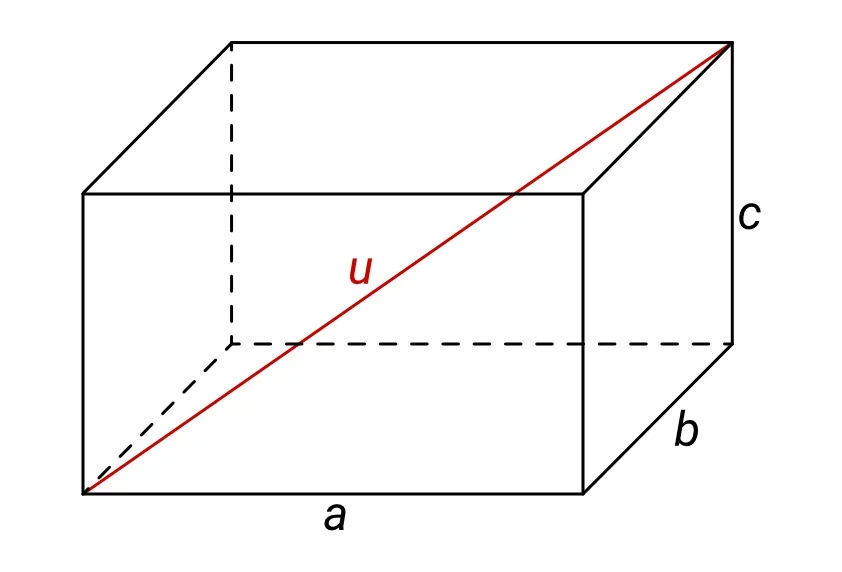
Pro výpočet jeho tělesové úhlopříčky můžeme použít zobecněnou Pythagorovu větu, kdy jednoduše přidáme druhou mocninu délky třetí strany c pod odmocninu ve vzorci – úplně stejně, jako tam máme druhé mocniny délek stran a a b:

$$ u = \sqrt{a^2 + b^2 + c^2} $$

Stejný princip uplatníme při výpočtu vzdálenosti bodů v prostoru: do vzorce pro výpočet vzdálenosti bodů v rovině přidáme druhou mocninu rozdílu z-ových souřadnic těchto bodů (z-ové souřadnice mají v dolním indexu číslo 3).

Jak můžete vidět, vzorec pro výpočet vzdálenosti bodů v prostoru se od vzorce pro výpočet vzdálenosti bodů v rovině liší pouze tím, že pod odmocninou obsahuje třetí závorku pro třetí souřadnice daných bodů.

Opět si spočítáme příklad:

Příklad 3

Vypočítejte vzdálenost bodů A[4; 2; -4] a B[2; 3; -2].

Řešení

\begin{align*} |AB| &= \sqrt{(b_1 -a_1)^2 + (b_2 -a_2)^2+ (b_3 -a_3)^2} = \\ &= \sqrt{(2 -4)^2 + (3 -2)^2 + (-2 -(-4))^2} = \\ &= \sqrt{(-2)^2 + 1^2 + 2^2} = \sqrt{4 + 1 + 4} = \\ &= \sqrt{9} = 3 \end{align*}

Závěr

V tomto článku jsme si ukázali, jak se počítá vzdálenost dvou bodů, které jsou umístěny v kartézské soustavě souřadnic v rovině a v prostoru.

V následujícím článku budeme počítat souřadnice středu úsečky.