Při práci s různými druhy funkcí je velmi často našim úkolem uvést tzv. specifické vlastnosti dané funkce.
Snad vůbec nejdůležitější vlastností určité funkce je její definiční obor, kterým jsme se zabývali v předchozím článku.
Obor hodnot funkce
Další – dá se říci obdobnou – vlastností je obor hodnot. Obor hodnot funkce je množina všech možných hodnot y, které můžeme dostat jako výsledek funkčního předpisu, dosadíme-li do něj všechna možná x z definičního oboru této funkce.
Laicky řečeno, když si představíme funkci jako „černou skříňku“ (viz obr. níže), tak definiční obor je rozsah všech hodnot x na vstupu této skříňky, které do něj můžeme „bezpečně dosadit“, zatímco obor hodnot je rozsah hodnot y, které můžeme dostat na výstupu.
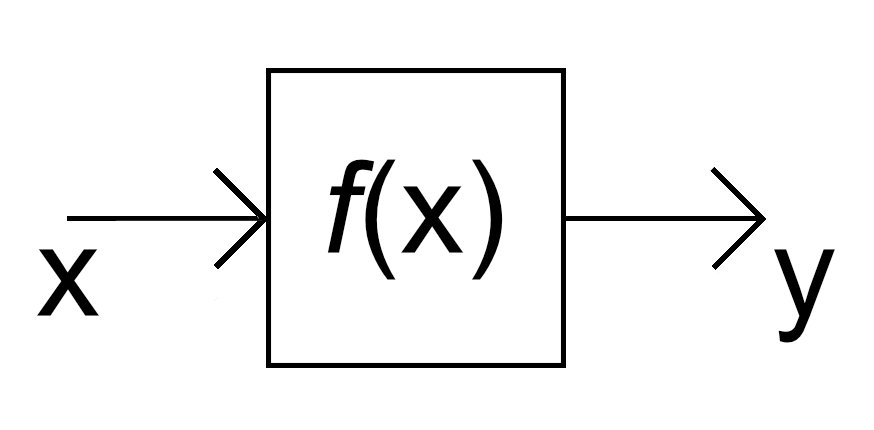
Jak definiční obor, tak i obor hodnot funkce, můžeme v mnoha případech snadno poznat z jejího grafu. Podívejme se znovu na příklad naší funkce z minulého článku týkající se závislosti doby volného pádu na výšce:
$$ y = \sqrt{\frac{2x}{9,81}} $$
které jsme přidělili následující definiční obor:
$$ D(f) = \langle 0; 500 \rangle $$
a sestrojili jsme její graf:
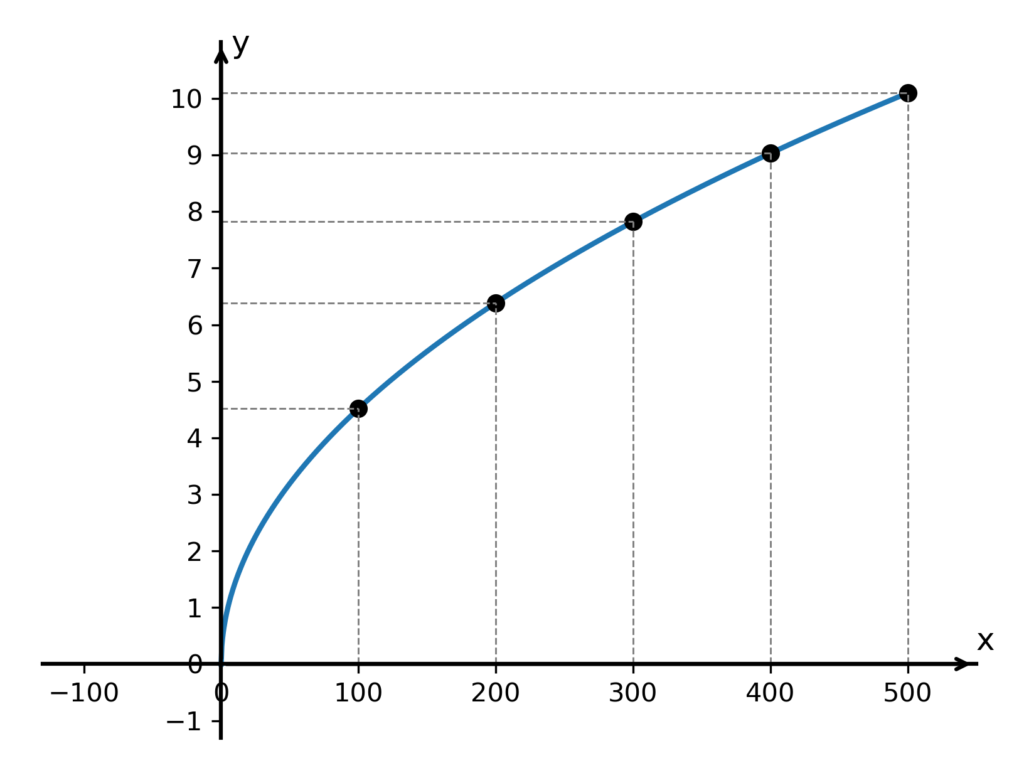
Z obrázku hned vidíme jak náš definiční obor (hodnoty x začínají na nule a končí na čísle 500), tak obor hodnot – nejmenší hodnota y je 0 a největší něco málo přes 10 (přesněji 10,10).
Jinak řečeno, budeme-li do předpisu funkce za x dosazovat všechny možné hodnoty od 0 do 500, budeme jako hodnoty y dostávat čísla v rozmezí od 0 do 10,10. Nikdy nezískáme hodnotu y, která by byla menší než 0 nebo větší než 10,10.
Obor hodnot funkce f se značí H(f) a v případě naší funkce ho můžeme zapsat pomocí intervalu takto:
$$ H(f) = \langle 0; 10{,}10 \rangle $$
Jako další příklad si uveďme funkci sinus. Jejím grafem je vlnovka, která neustále kmitá mezi čísly -1 a 1:

Pokud si její definiční obor sami neomezíme, pak ho budou tvořit všechna reálná čísla od minus nekonečna do plus nekonečna. Definiční obor, který tvoří všechna reálná čísla, můžeme zapsat buď pomocí následujícího intervalu:
$$ D(f) = (-\infty; +\infty) $$
nebo častěji ještě jednodušeji takto:
$$ D(f) = R $$
což znamená právě to, že definičním oborem jsou všechna čísla z oboru reálných čísel. Jinými slovy takovýto definiční obor není nijak omezen.
Oborem hodnot funkce sinus však budou pouze čísla někde v rozmezí -1 (včetně) a +1 (včetně) a můžeme ho zapsat takto:
$$ H(f) = \langle -1; 1 \rangle $$
Zkrátka ať dosadíme za x jakékoli číslo, které nás jen napadne, vždycky jako výslednou hodnotu y dostaneme nějaké číslo v intervalu $ \langle -1; 1 \rangle $. Nikdy se nestane, že bychom dostali např. y = 2.
Sudá a lichá funkce
Sudá funkce je taková funkce, že pro každou kladnou hodnotu x dostaneme vždy stejnou hodnotu y, jako pro zápornou hodnotu tohoto čísla x.
Znamená to, že pokud do funkce dosadíme za x např. číslo 4, vyjde nám stejná hodnota y, jako když dosadíme za x číslo -4, dosadíme-li za x číslo -7,5, vyjde nám stejná hodnota y, jako když dosadíme číslo -7,5 a úplně stejně to bude s každou dvojicí takových čísel. Jinými slovy nám vyjde vždy stejná hodnota y pro opačná čísla x (tj. čísla s opačným znaménkem).
Graf sudé funkce je osově souměrný (symetrický) podle osy y. (Osová souměrnost je jako zrcadlo – to, co vidím na levé straně, je zrcadlovým obrazem toho, co vidím vpravo.)

Lichá funkce je taková funkce, že pro zápornou hodnotu x dostaneme opačnou hodnotu y, než pro kladnou hodnotu tohoto čísla x.
V praxi to znamená, že když pro hodnotu x = 2 dostaneme hodnotu y = 8, tak pro hodnotu x = -2 dostaneme hodnotu y = -8. Nebo pokud pro hodnotu x = 2 dostaneme hodnotu y = -8, pak pro hodnotu x = -2 dostaneme hodnotu y = 8. A opět to tak bude s každou takovouto číselnou dvojicí.
Lépe si tuto vlastnost představíme pomocí grafu, protože graf liché funkce je středově souměrný podle počátku souřadného systému. (Středová souměrnost je jako hrací karta – když ji otočím vzhůru nohama, vidím stejný obrázek.)
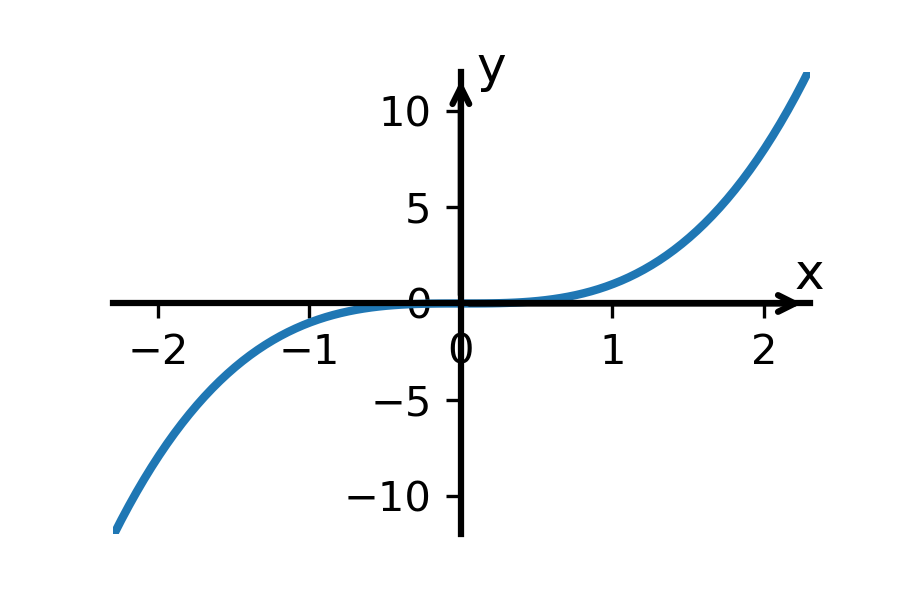
O funkci, která nemá ani jednu z těchto uvedených vlastností, říkáme, že není ani sudá ani lichá.
Periodická funkce
Periodická funkce je taková funkce, jejíž průběh se neustále opakuje.
Příkladem může být výše zmíněná funkce sinus. Když se na její průběh podíváme od nuly směrem doprava – tj. do kladných hodnot x, uvidíme kladnou půlvlnu, potom zápornou půlvlnu, za ní další kladnou půlvlnu úplně stejnou jako ta předchozí, potom opět zápornou půlvlnu rovněž úplně stejnou jako ta předchozí, a tak stále dokola.
Obdobné to bude, budeme-li průběh funkce sinus zkoumat od nuly směrem doleva, tedy do záporných hodnot x.

Zdola omezená, shora omezená a omezená funkce
Funkce je zdola omezená, pokud existuje určité číslo, pod které její funkční hodnoty y nikdy neklesnou. Veškeré hodnoty y z oboru hodnot této funkce budou větší než toto číslo nebo se mu maximálně budou rovnat.
Ukažme si příklad:
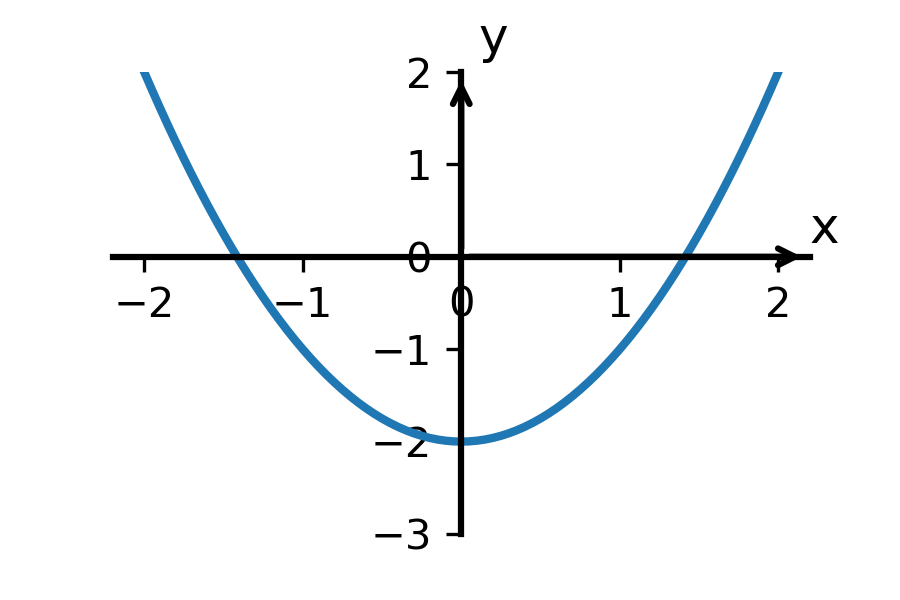
Vidíme, že graf funkce na obrázku nejdříve klesá, ale jakmile dosáhne své minimální hodnoty y = -2, začíná zase růst. Zkrátka ať za hodnotu x dosadíme jakékoli číslo z jejího definičního oboru, nikdy nám nevyjde taková hodnota y, která by byla menší než právě -2.
Funkce je shora omezená, pokud existuje určité číslo, nad které její funkční hodnoty y nikdy nevzrostou. Omezenost funkce shora je jednoduše opak omezenosti funkce zdola.
Opět si ukážeme příklad:

Vidíme obdobnou situaci jako u předchozího obrázku, jen tentokrát obráceně: graf funkce na tomto obrázku nejdříve roste, ale jakmile dosáhne hodnoty y = 2, začíná zase klesat, a tudíž nikdy nedostaneme hodnotu y větší než právě číslo 2.
O funkci říkáme, že je omezená, pokud je omezená zároveň zdola i shora.
Příkladem může být do třetice funkce sinus, tentokrát jen pro zpestření trochu upravené, aby rozptyl hodnot y – čili její obor hodnot – byl větší. Její funkční předpis je následující:
$$ f(x): y = 2 \sin x $$

Vidíme, že graf funkce na obrázku nikdy neklesne pod hodnotu -2 a současně nikdy nevzroste nad hodnotu 2.
Tady pozor na jedno pravidlo: O funkci nemůžeme říct, že je omezená, pokud je omezená pouze zdola (ale ne shora), nebo pouze shora (ale ne zdola). Teprve v případě, kdy je omezená zdola a současně i shora, můžeme říct, že je omezená (bez přívlastku).
Rostoucí a klesající funkce
Funkce je rostoucí, pokud pro libovolná dvě čísla x1 a x2 z jejího definičního oboru platí, že je-li x2 větší než x1, pak funkční hodnota y2 = f(x2) bude větší než funkční hodnota y1 = f(x1).
Jinak řečeno, budeme-li zvyšovat hodnoty x, budou se zvyšovat i hodnoty y. Nejlépe to poznáme z jejího grafu. Pokud si ho budeme prohlížet zleva doprava, uvidíme křivku, která stále roste – někdy více, někdy méně strmě, ale nikde ani na chvíli neklesá ani se nedrží na konstantní hodnotě.

Můžete si to také představit tak, že křivka je půda nějakého terénu, po kterém jdete. A pokud jdete stále nahoru, ani na chvíli neklesáte, ani nikde nejdete po rovině, je funkce rostoucí.
Funkce je klesající, pokud pro libovolná dvě čísla x1 a x2 z jejího definičního oboru platí, že je-li x2 větší než x1, pak funkční hodnota y2 = f(x2) bude menší než funkční hodnota y1 = f(x1).
Jinak řečeno, budeme-li zvyšovat hodnoty x, hodnoty y se budou naopak snižovat. Opět to dobře poznáme z grafu funkce – pokud si ho budeme prohlížet zleva doprava, uvidíme křivku, která stále klesá, nikde ani na chvíli neroste ani se nedrží na konstantní hodnotě.

V naší analogii s terénem stále klesáte, ale ani na chvíli nestoupáte, ani nikde nejdete po rovině.
Neklesající a nerostoucí funkce
Funkce je neklesající, pokud pro libovolná dvě čísla x1 a x2 z jejího definičního oboru platí, že je-li x2 větší než x1, pak funkční hodnota y2 = f(x2) bude větší nebo rovna než funkční hodnota y1 = f(x1).
Na první pohled jde o stejnou definici, jako u rostoucí funkce. Rozdíl je ve slovech „nebo rovna“. Budeme-li zvyšovat hodnoty x, hodnoty y se buď budou zvyšovat také, nebo alespoň budou zůstávat stejné. Funkce zkrátka neustále roste, ale v určitých úsecích se může držet na konstantní hodnotě.

Když si znovu představíme křivku funkce jako terén, po kterém jdeme zleva doprava, tak v případě neklesající funkce buď stoupáte, nikdy ani na chvíli neklesáte, ale chvílemi můžete jít i po rovině.
Funkce je nerostoucí, pokud pro libovolná dvě čísla x1 a x2 z jejího definičního oboru platí, že je-li x2 větší než x1, pak funkční hodnota y2 = f(x2) bude menší nebo rovna než funkční hodnota y1 = f(x1).
Nyní jde o podobnou definici jako u klesající funkce, a opět je rozdíl pouze ve slovech „nebo rovna“. Budeme-li zvyšovat hodnoty x, hodnoty y se budou buď zmenšovat, nebo alespoň budou zůstávat stejné. Funkce zkrátka neustále klesá, ale v určitých úsecích se může držet na konstantní hodnotě.

V naší analogii s terénem buď klesáte, nikdy ani na chvíli nestoupáte, ale chvílemi můžete jít i po rovině.
Rozdíl mezi rostoucí a neklesající funkcí, nebo mezi klesající a nerostoucí funkcí, tedy spočívá v tom, že v průběhu funkce buď jsou nebo nejsou povoleny konstantní úseky, kde se funkce drží na stejné hodnotě.
Z výše uvedeného také vyplývá, že každá rostoucí funkce je současně neklesající, a každá klesající funkce je současně nerostoucí, ale opačně to neplatí.
Monotónní funkce
Je-li nějaká funkce na celém svém definičním oboru neklesající, resp. nerostoucí, pak se souhrnně nazývá monotónní.
Je-li nějaká funkce na celém svém definičním oboru rostoucí, resp. klesající, pak se souhrnně nazývá ryze monotónní.
Prostá funkce
Poslední důležitou vlastností, kterou si dnes probereme, je to, zda je či není funkce tzv. prostá.
Podívejme se na následující graf funkce:

Zvolíme-li si libovolné číslo x z definičního oboru funkce, dostaneme právě jedno číslo y. To je v souladu s definicí funkce. Kdyby tomu tak nebylo, kdybychom dostali například dvě různá čísla y, nejednalo by se o funkci.
Z obrázku vidíme, že pokud si za x zvolíme např. číslo 1, dostaneme y = 2, zvolíme-li si za x číslo 2, dostaneme y = 4, nebo pro x = 3 dostaneme y = 8. (Viz šedé šipky.)
Ale co kdybychom chtěli postupovat opačně? Tzn. že bychom z výsledného čísla y chtěli zpětně určit, z jakého čísla x jsme ho dostali? Vidíme, že i to je v tomto případě možné. Např. číslo y = 8 jsme získali z čísla x = 3, číslo y = 4 jsme získali z čísla x = 2, nebo číslo y = 2 jsme získali z čísla x = 1. (Viz červené šipky v obrázku.)
A právě když platí nejen to, že funkce přiřazuje každému číslu x právě jedno číslo y, ale současně platí i to, že ke každému číslu y lze zpětně přiřadit právě jedno číslo x, ze kterého toto číslo y vzniklo, říkáme, že funkce je prostá.
Funkce na obrázku výše je tedy prostá, protože ke každému číslu y lze zpětně přiřadit právě jedno číslo x, ze kterého jsme toto číslo y získali.
Nyní se podívejme na jiný graf funkce:

Stále jde o zcela právoplatný graf funkce, protože platí, že ke každému číslu x funkce přiřadí právě jedno číslo y. Například číslu x = -1 přiřadí y = 1, číslu x = 2 přiřadí y = 4, nebo číslu x = 3 přiřadí číslo y = 9. (Viz šedé šipky v obrázku.)
Ale zároveň vidíme, že opačně to neplatí, tzn. že není pravda, že ke každému číslu y lze zpětně přiřadit právě jedno číslo x, ze kterého jsme toto číslo y získali. Například číslo y = 4 můžeme získat z čísla x = 2, ale také z čísla x = -2. Tudíž existují hned dvě čísla x, kterým funkce přiřadí hodnotu y = 4. Úplně stejně jsme na tom ze všemi jinými čísly y z oboru hodnot funkce kromě čísla 0. Zkrátka kromě nuly každé číslo y můžeme získat ze dvou různých čísel x, nikoli právě z jednoho. (Viz červené šipky v obrázku.)
Jestliže existuje aspoň jedno číslo y, které funkce přiřazuje více než jednomu číslu x, pak taková funkce není prostá. A to platí i pro naši funkci na obrázku výše.
Uveďme si ještě jeden příklad funkce, která není prostá – je to funkce sin(x):
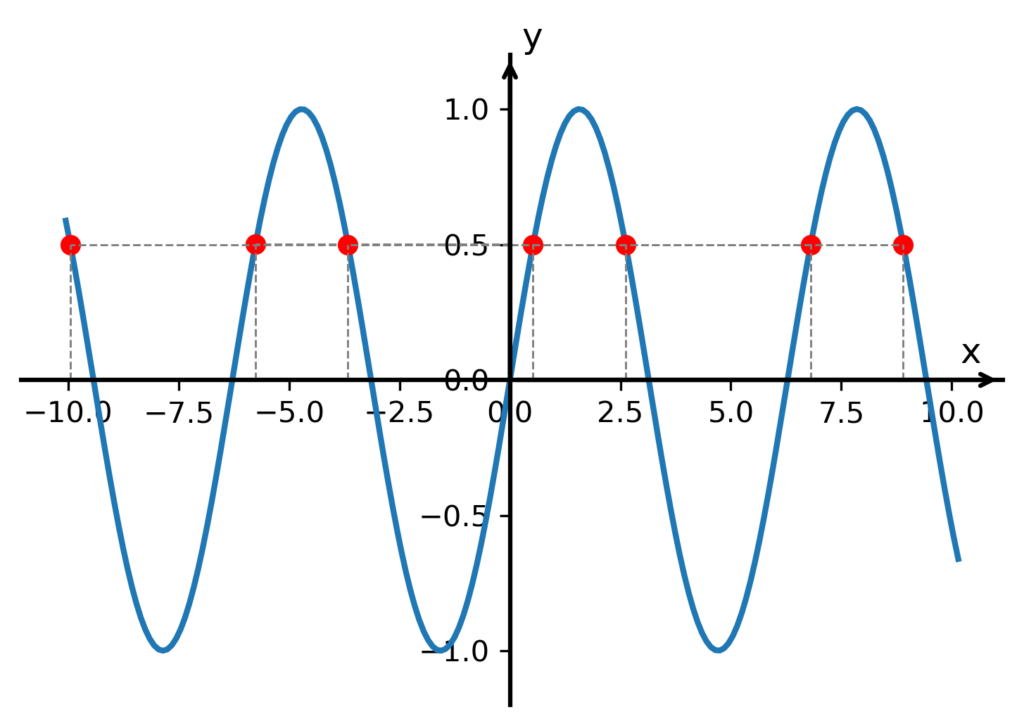
Vidíme, že zvolíme-li si hodnotu y = 0,5, můžeme ji získat z mnoha různých hodnot x. Obrázek zachycuje jen část průběhu funkce sinus, který bychom mohli protáhnout na levé i pravé straně do nekonečna. A tak existuje dokonce nekonečně mnoho různých hodnot x, pro které získáme hodnotu y = 0,5.
Na závěr uveďme, že každá funkce, která je na celém svém definičním oboru rostoucí nebo klesající, je současně prostá.
Maximum a minimum funkce
Jestliže existuje hodnota x taková, že příslušná hodnota y má zde z celého průběhu funkce největší hodnotu, říkáme, že funkce má v tomto bodě maximum.
Obdobně platí, že jestliže existuje hodnota x taková, že příslušná hodnota y má zde z celého průběhu funkce nejmenší hodnotu, říkáme, že funkce má v tomto bodě minimum.
Tímto bodem, kde má funkce maximum, resp. minimum, nemyslíme hodnotu y, ale číslo x, jehož dosazením do předpisu funkce tato největší, resp. nejmenší, hodnota y vznikne.
Závěr
V tomto článku jsme si probrali opravdu hodně specifických vlastností funkcí, ale není třeba to hned výborně znát. V následujících článcích budeme probírat konkrétní druhy funkcí a u každé z nich si tyto vlastnosti stanovíme, takže se k nim budeme opakovaně vracet. V následujícím článku začneme nejjednodušší z těchto funkcí, kterou je lineární funkce.
Uvidíte, že jakmile budete znát alespoň některé z těchto konkrétních druhů funkcí, zde popsané vlastnosti se pro vás stanou jednoduchým a intuitivním tématem.


