Vektorový součin vektorů - Matematika nejen pro střední školy

V předchozím článku jsme se zabývali skalárním součinem vektorů a jeho souvislostí s úhlem vektorů.

V tomto článku se podíváme na poslední základní aritmetickou operaci s vektory, kterou je vektorový součin vektorů.

Vektorový součin vektorů se často používá např. ve fyzice k vyjádření velikosti a směru „točivých“ veličin, jako např. moment síly apod.

Vektorový součin dvou vektorů nemůžeme provést pouze v rovině, protože jeho výsledkem je vektor, který je kolmý na oba násobené vektory. Tzn. že kdybychom si tyto vektory nakreslili např. do vodorovné roviny, výsledný vektor by směřoval z této roviny kolmo vzhůru nebo kolmo dolů. Proto vektorový součin vektorů můžeme provádět až s vektory v prostoru.

Geometrické vlastnosti vektorového součinu

Uvedeme si nejdřív geometrické vlastnosti vektorového součinu a až potom si ukážeme, jak se jeho souřadnice vypočítají ze souřadnic násobených vektorů.

Vektorový součin dvou vektorů, které leží na jedné přímce, je nulový vektor. Vektorový součin dvou vektorů u, v neležících na jedné přímce je vektor w, který má tyto vlastnosti:

vektor w je kolmý k oběma vektorům u, v,
vektory u, v, w tvoří pravotočivou bázi,
$ |\boldsymbol{w}| = |\boldsymbol{u}||\boldsymbol{v}| \sin \alpha $, kde $ \alpha $ je úhel vektorů u, v.

Vektorový součin w vektorů u, v značíme $ \boldsymbol{u} \times \boldsymbol{v} $, tj. $ \boldsymbol{w} = \boldsymbol{u} \times \boldsymbol{v} $.

Použili jsme pojem „pravotočivá báze“, který si musíme vysvětlit. Báze v prostoru je uspořádaná (tzn. záleží na pořadí) trojice vektorů, které neleží v jedné rovině. Například bázi tvořenou vektory a, b, c bychom označily jako (a, b, c).

Na následujícím obrázku je znázorněna báze z násobených vektorů u, v a jejich vektorového součinu w, které tvoří uspořádanou trojici (u, v, w):

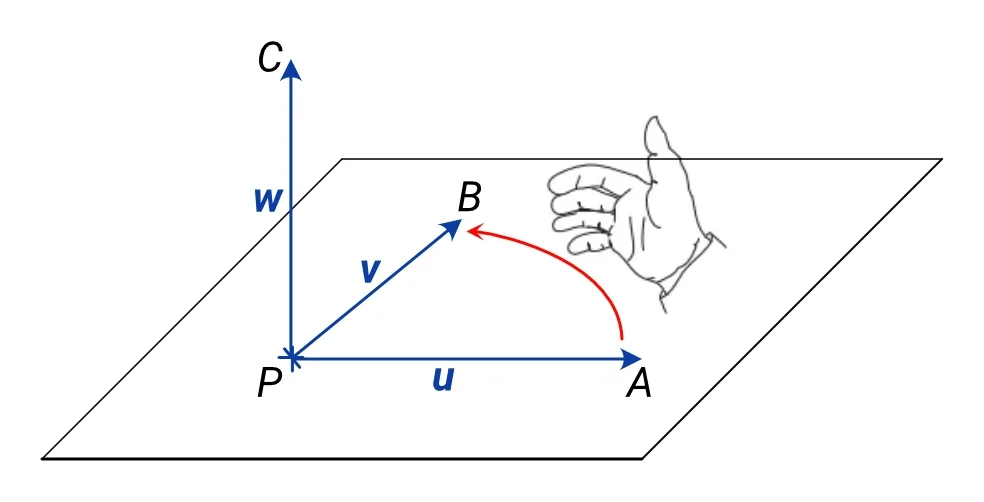
Pravotočivá báze se někdy určuje pomocí pravidla pravé ruky: když položíme pravou ruku na rovinu, ve které leží vektory u, v, tak jak je zobrazená na obrázku, tedy aby dlaň od zápěstí po konečky prstů směřovala od konce prvního vektoru v bázi (na obrázku bod A) po konec druhého vektoru v bázi (na obrázku bod B), tak třetí vektor v bázi bude směřovat ve směru vztyčeného palce – na obrázku tedy nahoru.

Z toho mj. plyne, že vektorový součin vektorů není komutativní, tzn. záleží na pořadí násobených vektorů. Kdybychom prohodili jejich pořadí tak, že místo vektorového součinu $ \boldsymbol{u} \times \boldsymbol{v} $ bychom měli součin $ \boldsymbol{v} \times \boldsymbol{u} $, pak výsledný vektor w by na obrázku směřoval dolů. Jeho velikost by však zůstala stejná, pouze směr by byl opačný. Z toho plyne následující:

Pro každé dva vektory u, v platí

$$ \boldsymbol{v} \times \boldsymbol{u} = -\boldsymbol{u} \times \boldsymbol{v} $$

Dále jste si určitě všimli, že pro vektorový součin místo symbolu tečky používáme symbol $ \times $. To je z toho důvodu, abychom rozlišili skalární součin od vektorového.

Nakonec bod č. 3 v rámečku říká, že velikost výsledného vektoru w je součinem velikostí násobených vektorů u, v krát sinus úhlu, který tyto vektory svírají. Z toho vyplývá, že čím blíže bude tento úhel nule nebo 180 stupňům, tím bude mít výsledný vektor menší velikost, protože pro tyto úhly se jejich sinus blíží nule. Naopak největší velikost bude výsledný vektor mít tehdy, když násobené vektory budou svírat pravý úhel.

Kdybychom tedy vektorem v otáčeli, přičemž bychom začali v poloze, při které by měl stejný směr jako vektor u, tak na začátku tohoto otáčení by měl výsledný vektor w nulovou velikost. Čím více bychom se blížili pravému úhlu, tím by byl výsledný vektor w větší, při pravém úhlu největší, a při pokračování otáčení by se zase zmenšoval, až při 180 stupních (tj. kdy by vektor v by směřoval přesně do opačného směru než vektor u) by velikost výsledného vektoru w opět klesla na nulu.

Výpočet vektorového součinu ze souřadnic vektorů

Vektorový součin vektorů u, v můžeme vypočítat pomocí následujícího vzorce:

\[ \boldsymbol{u} \times \boldsymbol{v} = (u_2v_3 -u_3v_2; u_3v_1 -u_1v_3; u_1v_2 -u_2v_1) \]

Tento vzorec je na zapamatování poměrně komplikovaný. V jeho zápisu se ale vyskytuje určitý vzor, který vám může pomoci si ho zrekonstruovat, jako například:

každý výraz odpovídající konkrétní souřadnici výsledného vektoru neobsahuje v dolních indexech právě takové číslo, kolikátou souřadnici počítáme,
symboly u a v se ve vzorci neustále střídají,
čísla v dolních indexech u symbolů u a v v prvních i druhých členech výrazů, které odpovídají jednotlivým souřadnicím výsledného vektoru, se ve vzorci směrem zleva doprava zvětšují o jedničku, přičemž jsou uzavřeny do kruhu, takže jakmile dosáhnou trojky, vrátí se posléze na jedničku.

Existuje však názornější způsob, jak si vzorec pro vektorový součin vektorů sestavit. V kartézské soustavě souřadnic v prostoru zavedeme pravotočivou bázi jednotkových (tj. o velikosti 1) vektorů e₁, e₂, e₃ tak, že všechny umístíme do počátku této soustavy souřadnic, přičemž vektor e₁ bude směřovat ve směru osy x, vektor e₂ ve směru osy y a vektor e₃ ve směru osy z – viz následující obrázek:

Libovolný vektor v prostoru můžeme vyjádřit jako součet násobků těchto jednotkových vektorů e₁, e₂, e₃, např. vektor u = (u₁; u₂; u₃) můžeme zapsat jako

\[ \boldsymbol{u} = u_1 \boldsymbol{e}_1 + u_2 \boldsymbol{e}_2 + u_3 \boldsymbol{e}_3 \]

Vektorový součin vektorů u, v provedeme následovně:

Vytvoříme si jednoduchou tabulku o tří řádcích a pěti sloupcích. Do prvních třech sloupců prvního řádku napíšeme naše jednotkové vektory e₁, e₂, e₃, do prvních třech sloupců druhého řádku souřadnice vektoru u, tedy symboly u₁, u₂, u₃ a do prvních třech sloupců třetího řádku souřadnice vektoru v, tedy symboly v₁, v₂, v₃. Do čtvrtého a pátého sloupce tabulky opíšeme symboly z jejího prvního a druhého sloupce.

Dále si nakreslíme si (nejlépe rozdílnými barvami) šikmé čáry klesající zleva doprava a zprava doleva, které protnou symboly v tabulce. Výsledná tabulka bude vypadat následovně:

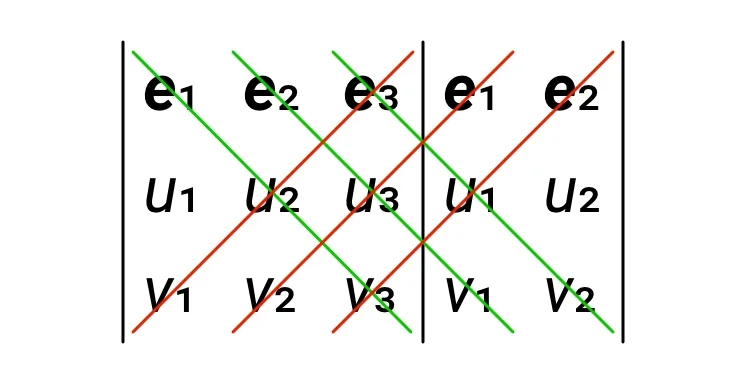
Na obrázku máme čáry klesající zleva doprava nakreslené zeleně a čáry klesající zprava doleva nakreslené červeně. Nyní vyjádříme vektorový součin vektorů u, v tak, že symboly ležící na každé jedné čáře vynásobíme, přičemž u členů vzniklých ze zelených čar bude znaménko plus a u členů vzniklých z červených čar bude znaménko minus. Symboly jednotkových vektorů e₁, e₂, e₃ budeme psát na konec každého členu. Dostaneme tak následující výraz:

\begin{align*} \boldsymbol{u} \times \boldsymbol{v} &= u_2v_3 \boldsymbol{e}_1 + u_3v_1 \boldsymbol{e}_2 + u_1v_2 \boldsymbol{e}_3 \; – \\ &-u_2v_1 \boldsymbol{e}_3 -u_3v_2 \boldsymbol{e}_1 -u_1v_3 \boldsymbol{e}_2 \end{align*}

Výraz upravíme vytknutím symbolů e₁, e₂, e₃, které napíšeme za závorky:

\[ \boldsymbol{u} \times \boldsymbol{v} = (u_2v_3 -u_3v_2) \boldsymbol{e}_1 + (u_3v_1 -u_1v_3) \boldsymbol{e}_2 + (u_1v_2 -u_2v_1) \boldsymbol{e}_3 \]

Člen se symbolem e₁ odpovídá první (x-ové) souřadnici výsledného vektoru, člen se symbolem e₂ jeho druhé (y-ové) souřadnici a člen se symbolem e₃ jeho třetí (z-ové) souřadnici. Ukážeme si příklad:

Příklad

Pro vektory u = (1; 3; -1), v = (2; 4; 5) vypočítejte vektorový součin $ \boldsymbol{u} \times \boldsymbol{v} $.

Řešení

Souřadnice vektorů u, v si napíšeme rovnou do tabulky podle schématu na obrázku výše:

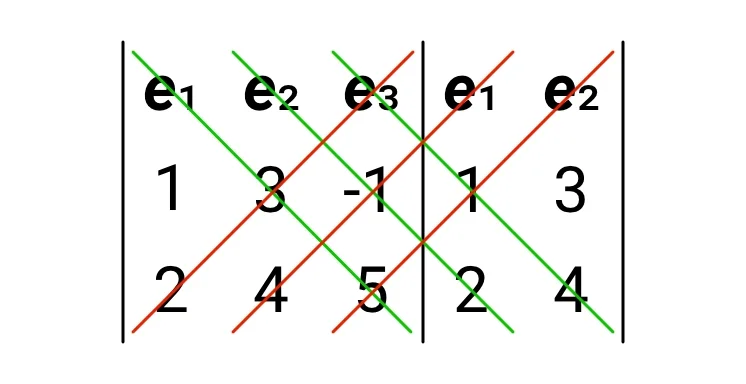
Nyní sestavíme závorku s těmi čísly, u kterých prochází čáry symbolem e₁ (první zelená a druhá červená čára), dále závorku s čísly, u nichž prochází čáry symbolem e₂ (druhá zelená a třetí červená čára), a nakonec závorku s čísly, u nichž prochází čáry symbolem e₃ (třetí zelená a první červená čára). V každé závorce bude jeden člen s čísly ležícími na jedné zelené čáře a jeden člen s čísly ležícími na jedné červené čáře. Tato čísla se spolu budou násobit, přičemž členy odpovídající červeným čarám se budou v dané závorce odčítat od členů odpovídajícím zeleným čarám. Za každou závorku napíšeme příslušný symbol e₁, e₂ nebo e₃ (sledujte obrázek!):

\begin{align*} \boldsymbol{u} \times \boldsymbol{v} &= (3 \cdot 5 -(-1) \cdot 4) \boldsymbol{e}_1 + ((-1) \cdot 2 -1 \cdot 5) \boldsymbol{e}_2 + (1 \cdot 4 -3 \cdot 2) \boldsymbol{e}_3 = \\ &= (15 + 4) \boldsymbol{e}_1 + (-2 -5) \boldsymbol{e}_2 + (4 -6) \boldsymbol{e}_3 = \\ &= 19 \boldsymbol{e}_1 -7 \boldsymbol{e}_2 -2 \boldsymbol{e}_3 \end{align*}

Souřadnice výsledného vektoru jsou tedy (19; -7; -2).

Závěr

V tomto článku jsme probrali vektorový součin vektorů a ukázali si, jak se dá vypočítat. Tím jsme zakončili přehled všech základních operací, které s vektory můžeme provádět, a vytvořili si pevný základ pro celou analytickou geometrii.