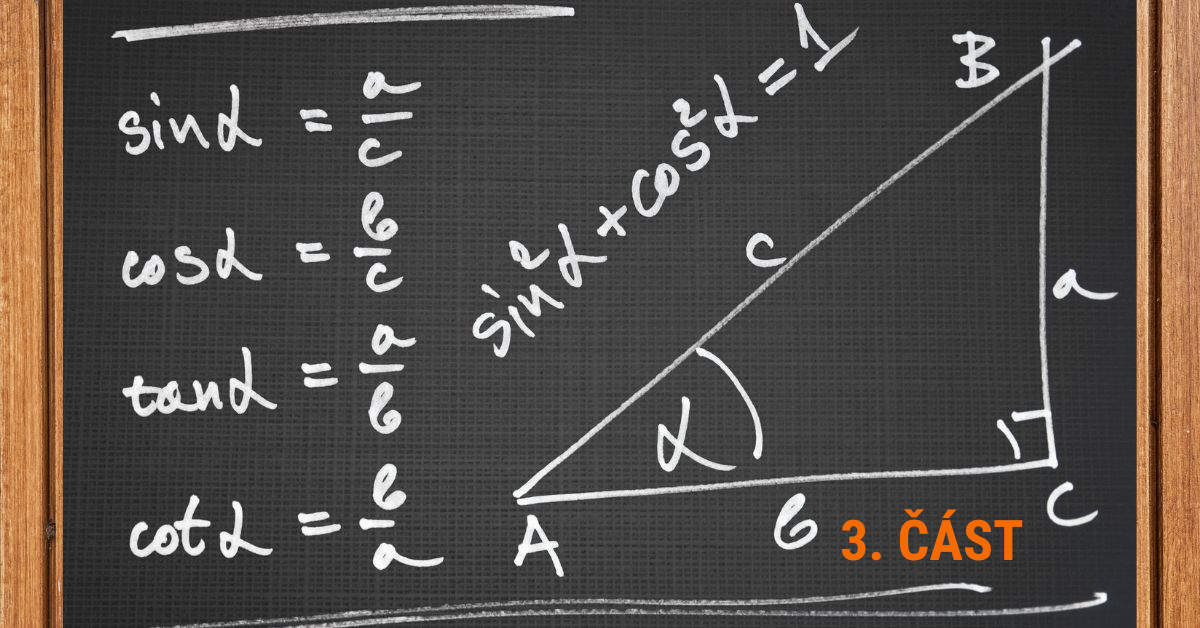V předchozím článku jsme si spočítali hodnoty goniometrických funkcí pro úhly o velikosti 30°, 45° a 60°.
V tomto článku se zaměříme na více „klasické“ příklady z trigonometrie pravoúhlého trojúhelníku, se kterými se určitě ve škole setkáte, a dané principy budete často potřebovat i v dalších geometrických úlohách.
Následující příklady se budou týkat pravoúhlého trojúhelníku ABC s klasickým značením s pravým úhlem při vrcholu C jako na následujícím obrázku:

Budeme mít zadány délku nebo délky některých stran a velikost vybraného úhlu, přičemž naším cílem bude spočítat délky zbývajících stran a úhlů, tj. těch, které zadány nebudou.
Příklad 1
a = 5 cm,
$ \alpha $ = 30°
b = ?
c = ?
$ \beta $ = ?
Protože v pravoúhlém trojúhelníku vždy platí, že součet ostrých úhlů, které jsou přilehlé k jeho přeponě, je roven 90° (v našem případě se jedná o úhly $ \alpha $ a $ \beta $, tak pokud známe velikost jednoho z těchto úhlů, snadno si spočítáme velikost druhého:
\begin{align*}
\alpha + \beta &= 90^\circ \qquad |- \; \alpha \\
\beta &= 90^\circ \; – \; \alpha \\
\beta &= 90^\circ \; – \; 30^\circ \\
\beta &= 60^\circ
\end{align*}
Dále si můžeme spočítat například délku strany c. Známe délku strany a, takže potřebujeme takovou goniometrickou funkci, která dává dohromady právě strany a a c. Takovou funkcí je sinus, takže platí:
\begin{align*}
\sin \alpha &= \frac{a}{c} \qquad | \cdot c \\
c \cdot \sin \alpha &= a \qquad |: \sin \alpha \\
c &= \frac{a}{\sin \alpha} \\
c &= \frac{5}{\sin 30^\circ} \\
c &= \frac{5}{\frac{1}{2}} \\
c &= 5 \cdot \frac{2}{1} \\
c &= 10 \text{ cm}
\end{align*}
Zbývá spočítat délku strany b. K tomu bychom mohli použít také nějakou goniometrickou funkci, ale jelikož už známe délky dvou stran pravoúhlého trojúhelníku, tu třetí si můžeme spočítat pomocí Pythagorovy věty. V našem případě budeme počítat délku odvěsny, takže budeme odčítat:
\begin{align*}
b^2 &= c^2 \; – \; a^2 \\
b &= \sqrt{c^2 \; – \; a^2} \\
b &= \sqrt{10^2 \; – \; 5^2} \\
b &= \sqrt{100 \; – \; 25} \\
b &= \sqrt{75} \\
b &\doteq 8{,}66 \text{ cm}
\end{align*}
Příklad 2
a = 8 cm
$ \beta $ = 45°
b = ?
c = ?
$ \alpha $ = ?
Opět začneme úhlem. Známe velikost úhlu $ \beta $, a protože musí platit $ \alpha + \beta = 90^\circ$, velikost úhlu $ \alpha $ bude:
$$ \alpha = 90^\circ \; – \; 45^\circ = 45^\circ $$
Jelikož jsou oba úhly přilehlé k přeponě shodné, znamená to, že tento pravoúhlý trojúhelník je současně rovnoramenný. Tím pádem obě odvěsny mají stejnou délku. Délku odvěsny a máme zadánu – je to 8 cm, takže délka odvěsny b bude také 8 cm.
Kdybychom se o tom chtěli přesvědčit výpočtem, tak budeme potřebovat takovou goniometrickou funkci, která dává dohromady obě odvěsny a, b. Takovou funkcí je např. tangens (ale i kotangens, ale tangens se používá běžněji):
\begin{align*}
\DeclareMathOperator{\tg}{tg} \\
\tg \alpha &= \frac{a}{b} \qquad | \cdot b \\
b \cdot \tg \alpha &= a \qquad |: \tg \alpha \\
b &= \frac{a}{\tg \alpha} \\
b &= \frac{8}{\tg 45^\circ} \\
b &= \frac{8}{1} \\
b &= 8 \text{ cm}
\end{align*}
Zbývá spočítat délku strany c. Jelikož známe délky obou zbývajících stran, můžeme použít Pythagorovu větu. Strana c je přepona, takže budeme sčítat:
\begin{align*}
c^2 &= a^2 + b^2 \\
c &= \sqrt{a^2 + b^2} \\
c &= \sqrt{8^2 + 8^2} \\
c &= \sqrt{64 + 64} \\
c &= \sqrt{128} \\
c &\doteq 11{,}31 \text{ cm}
\end{align*}
Příklad 3
a = 6 cm
c = 12 cm
b = ?
$ \alpha $ = ?
$ \beta $ = ?
Nyní známe délky dvou stran (jedné odvěsny a přepony), ale neznáme žádný úhel. Začneme tím, že si pomocí Pythagorovy věty spočítáme délku druhé odvěsny:
\begin{align*}
b^2 &= c^2 \; – \; a^2 \\
b &= \sqrt{c^2 \; – \; a^2} \\
b &= \sqrt{12^2 \; – \; 6^2} \\
b &= \sqrt{144 \; – \; 36} \\
b &= \sqrt{108} \\
b &\doteq 10{,}39 \text{ cm}
\end{align*}
Když teď známe délky všech tří stran pravoúhlého trojúhelníku, můžeme si spočítat velikost libovolného z úhlů pomocí jakékoli goniometrické funkce.
My jsme ale při výpočtu délky strany b provedli zaokrouhlení na dvě desetinná místa. Aby se nám neakumulovaly zaokrouhlovací chyby, bude lepší použít délky těch stran, které máme zadány – výsledek tak bude o něco přesnější. Protože máme zadány strany a, c, potřebujeme takovou goniometrickou funkci, která dává dohromady právě je. Jedná se o odvěsnu a přeponu, takže můžeme použít buď sinus nebo kosinus. Která z nich to bude, záleží na úhlu, jehož velikost chceme spočítat jako první, tzn. můžeme si vybrat. Platí:
$$ \sin \alpha = \frac{a}{c} $$
nebo také:
$$ \cos \beta = \frac{a}{c} $$
Rozhodneme se například, že nejdřív spočítáme velikost úhlu $ \alpha $ (můžete si zkusit spočítat napřed velikost úhlu $ \beta $):
\begin{align*}
\sin \alpha &= \frac{a}{c} \\
\sin \alpha &= \frac{6}{12} \\
\sin \alpha &= \frac{1}{2}
\end{align*}
Z předchozího článku víme, že když sinus $ \frac{1}{2} $ odpovídá úhlu o velikosti 30°. Proto:
$$ \alpha = 30^\circ $$
Velikost úhlu $ \beta $ tím pádem bude:
\begin{align*}
\beta &= 90^\circ \; – \; \alpha = \\
&= 90^\circ \; – \; 30^\circ = 60^\circ
\end{align*}
Příklad 4
c = 11 cm
$ \beta $ = 55°
a = ?
b = ?
$ \alpha $ = ?
Opět začneme úhlem:
\begin{align*}
\alpha &= 90^\circ \; – \; \beta \\
&= 90^\circ \; – \; 55^\circ = 35^\circ
\end{align*}
Protože známe délku přeponu, potřebujeme goniometrickou funkce sinus nebo kosinus. Spočítejme si jako první např. stranu b:
\begin{align*}
\cos \alpha &= \frac{b}{c} \qquad | \cdot c \\
c \cdot \cos \alpha &= b \\
b &=11 \cdot \cos 35^\circ
\end{align*}
Úhel o velikosti 35° nepatří mezi ty, jehož hodnoty goniometrických funkcí se běžně učí zpaměti – budeme potřebovat kalkulačku, do které zadáme $ 11 \times \cos 35 $ a získáme výsledek (pouze si pohlídejte, že máte kalkulačku nastavenou v režimu stupňů, a ne třeba radiánů):
$$ b \doteq 9{,}01 \text{ cm} $$
Délku strany a bychom si mohli opět spočítat pomocí Pythagorovy věty, ale spočítejme si ji pro změnu pomocí goniometrické funkce. Použijeme přeponu c, kterou máme zadánu, protože když jsme počítali délku odvěsny b, na konci jsme zaokrouhlovali, což by nám sice jen trochu, ale přece jen ovlivnilo přesnost výsledku.
Potřebujeme tedy goniometrickou funkci, která pracuje s přeponou, což je sinus nebo kosinus. Použijeme například sinus úhlu alfa:
\begin{align*}
\sin \alpha &= \frac{a}{c} \qquad | \cdot c \\
a &= c \cdot \sin \alpha \\
a &= 11 \cdot \sin 35^\circ
\end{align*}
Zadáme do kalkulačky $ 11 \times \sin 35 $ a dostaneme výsledek:
$$ a \doteq {6,31} \text{ cm} $$
Příklad 5
a = 8 cm
b = 5 cm
c = ?
$ \alpha $ = ?
$ \beta $ = ?
Máme zadány délky odvěsen. Délku přepony můžeme spočítat pomocí Pythagorovy věty:
\begin{align*}
c^2 &= a^2 + b^2 \\
c &= \sqrt{a^2 + b^2} \\
c &= \sqrt{8^2 + 5^2} \\
c &= \sqrt{64 + 25} \\
c &= \sqrt{89} \\
c &\doteq 9{,}43 \text{ cm}
\end{align*}
Protože nemáme zadánu velikost žádného z úhlů přilehlých k přeponě, musíme některou spočítat pomocí goniometrické funkce. Mohli bychom použít sinus nebo kosinus, které pracují s přeponou, ale její délku jsme si sami spočítali s tím, že jsme výsledek zaokrouhlili. Bude tedy o něco přesnější pracovat se zadanými hodnotami, což jsou délky odvěsen. Funkce, která dává dohromady odvěsny je např. tangens. Použijeme ho a spočítáme třeba úhel alfa:
\begin{align*}
\DeclareMathOperator{\tg}{tg} \\
\tg \alpha &= \frac{a}{b} \\
\tg \alpha &= \frac{8}{5} \\
\tg \alpha &= 1{,}6
\end{align*}
Máme hodnotu tangentu, která nepatří mezi ty nejznámější, jež jsme probírali v předchozím článku. Zde musíme opět použít kalkulačku, ale trochu jiným způsobem, než jsme to dělali v předchozích příkladech.
Když do kalkulačky zadáme např. tg 35 a zmáčkneme tlačítko =, zobrazí se hodnota funkce tangens pro úhel o velikosti 35°. Co když to ale chceme naopak? Tzn. zadat do kalkulačky hodnotu funkce tangens a zjistit, jakému úhlu tato hodnota odpovídá?
V takovém případě musíme použít funkci, která je na kalkulačce označená jako tg-1. To je inverzní funkce k funkci tangens, které se v matematice říká arkustangens, ale tím se teď nemusíme trápit. Zkrátka stiskneme tlačítko s funkcí tg-1, zadáme hodnotu tangentu, stiskneme = a zobrazí se velikost úhlu. V našem případě to bude:
\begin{align*} \DeclareMathOperator{\tg}{tg} \\ \tg \alpha &= 1,6 \implies \alpha = 57{,}99^\circ \doteq 58^\circ \end{align*}
Velikost úhlu beta spočítáme odečtením velikosti úhlu alfa od 90°:
$$ \beta = 90^\circ \; – \; 58^\circ = 32^\circ $$
Příklad 6
b = 7 cm
c = 9 cm
a = ?
$ \alpha = $ = ?
$ \beta $ = ?
Opět známe délky dvou stran – v tomto případě jedné z odvěsen a přepony, ale neznáme žádný úhel. Začneme výpočtem délky třetí strany pomocí Pythagorovy věty – počítáme délku odvěsny, takže budeme odečítat:
\begin{align*}
a^2 &= c^2 \; – \; b^2 \\
a &= \sqrt{c^2 \; – \; b^2} \\
a &= \sqrt{9^2 \; – \; 7^2} \\
a &= \sqrt{81 \; – \; 49} \\
a &= \sqrt{32} \\
a &\doteq 5{,}66 \text{ cm}
\end{align*}
Nyní spočítáme velikost některého z úhlů pomocí goniometrické funkce, jež dává dohromady odvěsnu a přeponu, které máme zadány (stejně jako v přechozích příkladech kvůli větší přesnosti). Zvolíme třeba kosinus úhlu alfa (můžete si zkusit zvolit sinus úhlu beta):
\begin{align*}
\cos \alpha &= \frac{b}{c} \\
\cos \alpha &= \frac{7}{9} \\
\cos \alpha &\doteq 0{,}7778
\end{align*}
Známe hodnotu kosinu, ale nevíme, jaké velikosti úhlu odpovídá. Musíme znovu použít kalkulačku podobným způsobem jako v předchozím příkladu:
Stiskneme tlačítko s funkcí cos-1, zadáme hodnotu kosinu 0,7778 (hodnoty goniometrických funkcí je dobré uchovávat s vyšší přesností, proto jsme ji zaokrouhlili na čtyři desetinná místa), stiskneme = a dostaneme výsledek:
\[ \cos \alpha = 0,77777778 \implies \alpha \doteq 38{,}9424^\circ \]
Pokud bychom chtěli tento výsledek místo desetinného čísla převést na celé stupně, úhlové minuty a úhlové vteřiny, tak dokud ho máme zobrazený na displeji kalkulačky, stiskneme tlačítko pro tento převod. Zpravidla je na něm symbol kolečka následované apostrofem následovaný dvěma apostrofy. V našem případě takto zapsaný výsledek bude:
$$ \alpha = 38^\circ 56^{\prime} 32{,}79^{\prime\prime} $$
Obvykle stačí, když velikost úhlu zaokrouhlíme s přesností na úhlové minuty. Jeden stupeň má 60 úhlových minut, proto musíme zaokrouhlovat nahoru už od třiceti úhlových vteřin, ne až od padesáti! Náš zaokrouhlený výsledek tedy bude vypadat takto:
$$ \alpha = 38^\circ 57^{\prime} $$
Nakonec spočítáme velikost úhlu beta jako obvykle tak, že velikost úhlu alfa odečteme od 90°:
$$ \beta = 90^\circ \; – \; 38^\circ 57^{\prime}= 51^\circ 3^{\prime} $$
Tento výpočet můžeme provést i zpaměti: Nejprve si uvědomíme, kolik úhlových minut chybí do nejbližšího vyššího úhlového stupně. V případě 38°57‘ jsou to 3‘. Poté spočítáme, kolik úhlových stupňů chybí od tohoto nejbližšího vyššího počtu stupňů do devadesáti. V případě 39° to je 51°. Těchto 51° a výše zmíněné 3‘ budou tvořit výsledek.
Závěr
V tomto článku jsme si spočítali šest příkladů na trigonometrii pravoúhlého trojúhelníku. Potřebovali jsme k tomu goniometrické funkce sinus, kosinus, tangens a Pythagorovu větu. Tím jsme zakončili sérii o pravoúhlém trojúhelníku ze základních poznatků.
Pokud jste si prošli sérii celou a věnovali se i příkladům, pak vám gratuluji, protože jste si pevně upevnily jedno ze základních témat celé matematiky!