V předchozím článku jsme si popsali základy trigonometrie pravoúhlého trojúhelníku. Konkrétně jsme si definovali sinus, kosinus, tangens a kotangens a řekli jsme si, jak si tyto definice lépe zapamatovat.
V tomto článku navážeme tím, že si spočítáme hodnoty sinu, kosinu, tangentu a kotangentu pro vybrané velikosti úhlů, které je určitě dobré znát zpaměti.
Sinus, kosinus, tangens a kotangens jako goniometrické funkce
Sinus (sin), kosinus (cos), tangens (tg) a kotangens (cotg) jsou z matematického hlediska funkce, kterým souhrnně říkáme goniometrické funkce a více se jim budeme věnovat v sérii článků o goniometrii.
Hodnoty goniometrických funkcí vůbec nezáleží na velikosti pravoúhlého trojúhelníku, pokud zachováme jeho tvar. Budeme-li totiž mít např. pravoúhlý trojúhelník s protilehlou odvěsnou k vybranému úhlu o délce 10 cm a přeponou o délce 20 cm, poměr délek této odvěsny a přepony (čili sinus daného úhlu) bude mít hodnotu $ \frac{10}{20} = \frac{1}{2} $. Zvětšíme-li trojúhelník např. třikrát, bude délka protilehlé odvěsny 30 cm a délka přepony 60 cm, ale poměr těchto délek (a tedy i sinus úhlu) zůstane stejný, protože i $ \frac{30}{60} = \frac{1}{2} $
Stejná hodnota sinus určitého úhlu znamená i stejnou velikost úhlu samotného. To samé platí pro ostatní goniometrické funkce, a proto můžeme říct, že hodnoty goniometrických funkcí závisí pouze na velikosti daného úhlu.
Spočítejme si hodnoty goniometrických funkcí pro vybrané velikosti úhlů v následujícím příkladu.
Pozn.: Jestli se vám nechce se těmito výpočty zabývat, přejděte rovnou na konec článku, kde najdete tyto hodnoty v přehledné tabulce. Nicméně následující příklad je velmi dobrý pro procvičení logického myšlení, představivosti a práce se zlomky včetně jejich usměrňování. Pokud si vezmete tužku a papír, uděláte si příslušné náčrtky a zkusíte si příklad spočítat spolu s jeho rozborem, značně to upevní vaše znalosti do budoucna. Navíc se dozvíte, proč jsou vybrané hodnoty goniometrických funkcí právě takové, jaké jsou.
Příklad
Vypočtěte hodnoty funkcí sinus, kosinus, tangens a kotangens pro úhly 30°, 45° a 60°.
Řešení
Sinus, kosinus, tangens a kotangens pro 30° a 60° určíme z rovnostranného trojúhelníku. Rovnostranný trojúhelník má všechny strany stejně dlouhé. Velikosti všech jeho úhlů jsou také stejné a sice 60°. Výška spuštěná z libovolného vrcholu na protilehlou stranu dopadne vždy přesně doprostřed této strany.
Nakresleme si takový trojúhelník, označme ho ABC, délku jeho strany označme jako a, spusťme výšku z bodu C na spodní stranu a bod, kam tato výška dopadne, označme P.
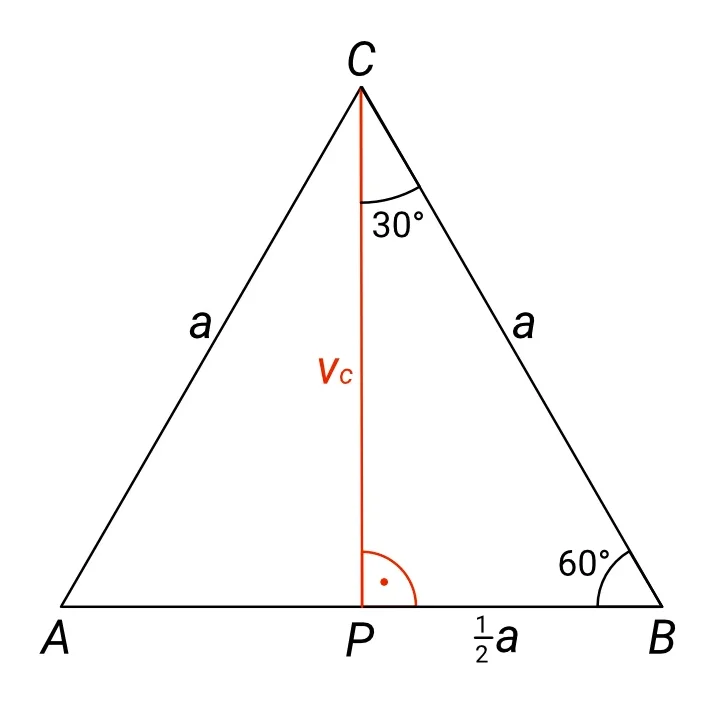
Výška nám rozdělí úhel při vrcholu C na dva poloviční úhly, tzn. že budou mít velikost 30°. Zároveň, protože výška dopadne na danou stranu vždy pod pravým úhlem, jsme získali trojúhelník BCP, který je pravoúhlý. A v pravoúhlém trojúhelníku platí goniometrické funkce tak, jak jsme je definovali výše.
Jednu odvěsnu tohoto trojúhelníku tvoří strana PC (výška), druhou odvěsnu strana PB o délce jedné poloviny strany a, tedy $ \frac{a}{2} $ (protože bod P, kam dopadla výška, je přesně v polovině strany AB) a přeponu tvoří strana BC o délce a.
Délku odvěsny PC můžeme určit z Pythagorovy věty:
\begin{align*}
|PC|^2 &= a^2 \; – \; \bigg(\frac{a}{2}\bigg)^2 = \\
&= a^2 \; – \; \frac{a^2}{4} = \frac{3}{4}a^2
\end{align*}
\begin{align*}
|PC| &= \sqrt{\frac{3}{4}a^2} = \sqrt{3} \cdot \sqrt{\frac{a^2}{4}} = \\
&= \sqrt{3} \cdot \frac{a}{2} = \frac{a}{2} \sqrt{3}
\end{align*}
Když nyní známe na obecné úrovni délky všech tří stran trojúhelníku BCP, můžeme určit hodnoty goniometrických funkcí úhlů 30° a 60° (sledujte výše uvedený obrázek):
\begin{align*}
\sin 30^\circ &= \frac{|PB|}{|BC|} = \frac{\frac{a}{2}}{a} = \\
&= \frac{a}{2} \cdot \frac{1}{a} = \frac{1}{2}
\end{align*}
\begin{align*}
\cos 30^\circ &= \frac{|PC|}{|BC|} = \frac{\frac{a}{2} \sqrt{3}}{a} = \\
&= \frac{a \sqrt{3}}{2} \cdot \frac{1}{a} = \frac{\sqrt{3}}{2}
\end{align*}
\begin{align*}
\sin 60^\circ &= \frac{|PC|}{|BC|} = \\
&= \cos 30^\circ = \frac{\sqrt{3}}{2}
\end{align*}
\begin{align*}
\cos 60^\circ &= \frac{|PB|}{|BC|} = \\
&= \sin 30^\circ = \frac{1}{2}
\end{align*}
\begin{align*}
\DeclareMathOperator{\tg}{tg} \\
\tg 30^\circ &= \frac{|PB|}{|PC|} = \frac{\frac{a}{2}}{\frac{a}{2} \sqrt{3}} \\
&= \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\end{align*}
\begin{align*}
\DeclareMathOperator{\cotg}{cotg} \\
\cotg 30^\circ &= \frac{|PC|}{|PB|} = \frac{\frac{a}{2} \sqrt{3}}{\frac{a}{2}} = \\
\\ &= \sqrt{3}
\end{align*}
\begin{align*}
\DeclareMathOperator{\tg}{tg} \\
\tg 60^\circ &= \frac{|PC|}{|PB|} = \\
&= \cotg 30^\circ = \sqrt{3}
\end{align*}
\begin{align*}
\DeclareMathOperator{\cotg}{cotg} \\
\cotg 60^\circ &= \frac{|PB|}{|PC|} = \\
&= \tg 30^\circ = \frac{\sqrt{3}}{3}
\end{align*}
Hodnoty těchto funkcí pro úhel 45° určíme z pravoúhlého rovnoramenného trojúhelníku ABC na následujícím obrázku:
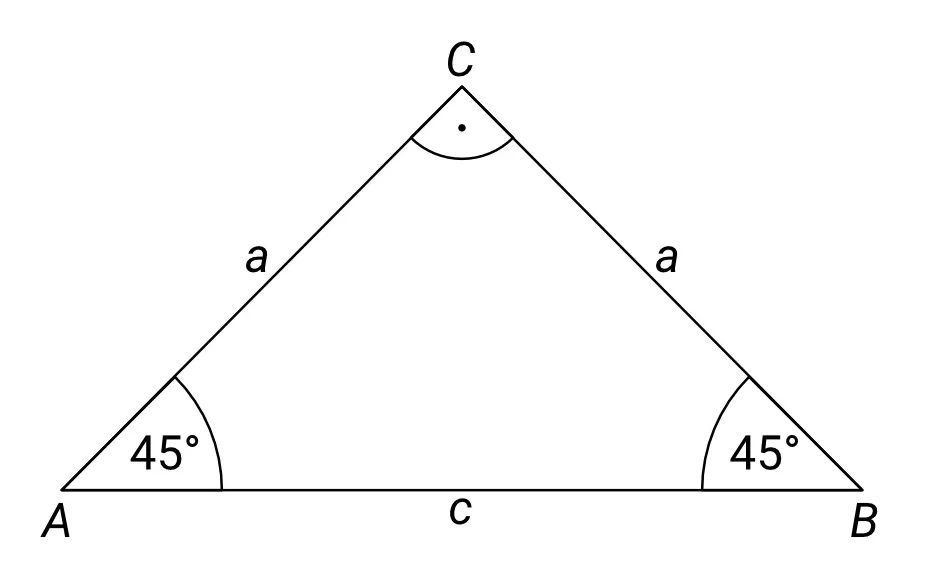
Je to vlastně polovina čtverce rozděleného podle jeho úhlopříčky. Ramena jsou odvěsny a mají délku a. Podle Pythagorovy věty můžeme spočítat délku strany c (což je de facto úhlopříčka zmíněného čtverce), která je přeponou:
\begin{align*}
c &= \sqrt{a^2 + a^2} = \sqrt{2a^2} = \\
&= \sqrt{2} \cdot \sqrt{a^2} = a \sqrt{2}
\end{align*}
Když nyní na obecné úrovni známe délky všech tří stran trojúhelníku ABC, můžeme opět spočítat výše zmíněné hodnoty:
\begin{align*}
\sin 45^\circ &= \frac{|BC|}{|AB|} = \frac{a}{a \sqrt{2}} = \\
&= \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\\
\end{align*}
\begin{align*}
\cos 45^\circ &= \frac{|AC|}{|AB|} = \frac{a}{a \sqrt{2}} = \\
&= \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\\
\end{align*}
Hodnoty funkcí sinus a kosinus pro úhel o velikosti 45° jsou tedy stejné.
Z tohoto trojúhelníku můžeme snadno spočítat i hodnoty funkcí tangens a kotangens pro 45°:
\[
\DeclareMathOperator{\tg}{tg} \\
\tg 45^\circ = \frac{|BC|}{|AC|} = \frac{a}{a} = 1
\]
\[
\DeclareMathOperator{\cotg}{cotg} \\
\cotg 45^\circ = \frac{|AC|}{|BC|} = \frac{a}{a} = 1
\]
Výsledky získané v tomto příkladu shrneme:
$$ \sin 30^\circ = \cos 60^\circ = \frac{1}{2} $$
$$ \sin 60^\circ = \cos 30^\circ = \frac{\sqrt{3}}{2} $$
$$ \sin 45^\circ = \cos 45^\circ = \frac{\sqrt{2}}{2} $$
\[
\DeclareMathOperator{\tg}{tg} \\
\DeclareMathOperator{\cotg}{cotg} \\
\tg 30^\circ = \cotg 60^\circ = \frac{\sqrt{3}}{3}
\]
\[
\DeclareMathOperator{\tg}{tg} \\
\DeclareMathOperator{\cotg}{cotg} \\
\tg 60^\circ = \cotg 30^\circ = \sqrt{3}
\]
\[
\DeclareMathOperator{\tg}{tg} \\
\DeclareMathOperator{\cotg}{cotg} \\
\tg 45° = \cotg 45° = 1
\]
Na závěr si uděláme ještě jedno shrnutí těchto hodnot ve formě přehledné tabulky:
| 30° | 45° | 60° | |
| sin | $ \frac{1}{2} $ | $ \frac{\sqrt{2}}{2} $ | $ \frac{\sqrt{3}}{2} $ |
| cos | $ \frac{\sqrt{3}}{2} $ | $\frac{\sqrt{2}}{2} $ | $ \frac{1}{2} $ |
| tg | $ \frac{\sqrt{3}}{3} $ | 1 | $ \sqrt{3} $ |
| cotg | $ \sqrt{3} $ | 1 | $ \frac{\sqrt{3}}{3} $ |
Závěr
V tomto článku jsme si řekli, že sinus, kosinus, tangens a kotangens jsou tzv. goniometrické funkce a spočítali jsme si jejich hodnoty pro velikosti úhlů 30°, 45° a 60°, které jsme shrnuli ve matematické podobě i ve formě tabulky. Jde právě o ty hodnoty, jejichž znalost se většinou vyžaduje znát zpaměti.
V následujícím článku si spočítáme několik „klasických“ příkladů na pravoúhlý trojúhelník ve spojení s goniometrickými funkcemi, se kterými se v různých oblastech matematiky určitě setkáte.