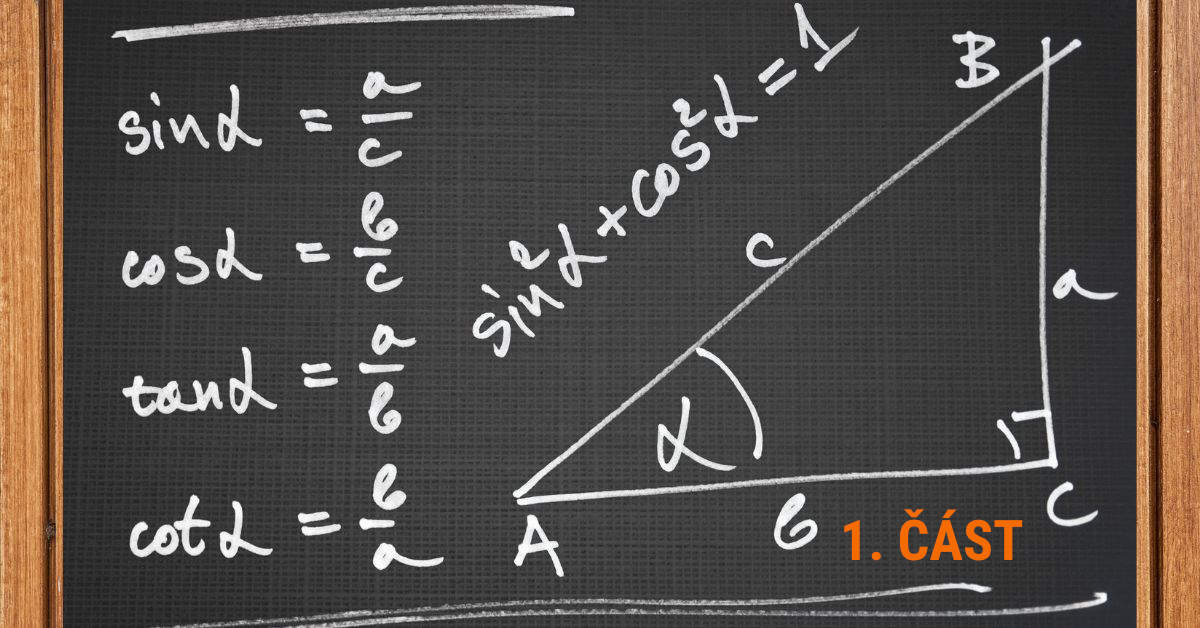V předchozím článku jsme si popsali Thaletovu větu.
V tomto článku se budeme věnovat trigonometrii pravoúhlého trojúhelníku. Trigonometrie se zabývá vztahy mezi stranami a úhly trojúhelníku. Existuje i trigonometrie obecného trojúhelníku, ale protože se v této sérii věnujeme pravoúhlému trojúhelníku, v následujícím textu se zaměříme právě na trojúhelník pravoúhlý.
Pravoúhlý trojúhelník ABC s obvyklým značením má stranu a naproti vrcholu A, stranu b naproti vrcholu B a stranu c naproti vrcholu C. Úhel $ \alpha $ (alfa) je u vrcholu A, úhel $ \beta $ (beta) je u vrcholu B a úhel $ \gamma $ (gama) je u vrcholu C a je pravý, tj. má 90°. Viz následující obrázek:

Strany a, b jsou tedy odvěsny a strana c je přepona.
Pythagorova věta nám umožňuje spočítat délku třetí strany pravoúhlého trojúhelníku, pokud známe délky zbývajících dvou stran. Ale my často neznáme délky dvou stran – místo toho známe například délku jedné strany a velikost některého úhlu, nebo známe třeba i délky všech tří stran, ale zajímá nás velikost určitého úhlu atp.
V takových situacích si už s Pythagorovou větou nevystačíme a potřebujeme nějaké jiné vztahy, které nám umožní spočítat to, co potřebujeme.
Tyto vztahy jsou následující:
Poměr délek odvěsny protilehlé k úhlu $ \alpha $ a přepony se nazývá sinus úhlu $ \alpha $:
$$ \sin \alpha = \frac{a}{c} $$
Poměr délek odvěsny přilehlé k úhlu $ \alpha $ a přepony se nazývá kosinus úhlu $ \alpha $:
$$ \cos \alpha = \frac{b}{c} $$
Poměr délek odvěsny protilehlé a odvěsny přilehlé k úhlu $ \alpha $ se nazývá tangens úhlu $ \alpha $:
\[
\DeclareMathOperator{\tg}{tg} \\
\tg \alpha = \frac{a}{b}
\]
Poměr délek odvěsny přilehlé a odvěsny protilehlé k úhlu $ \alpha $ se nazývá kotangens úhlu $ \alpha $: \[
\DeclareMathOperator{\cotg}{cotg} \\
\cotg \alpha = \frac{b}{a}
\]
Jak si to lépe zapamatovat
Samozřejmě v jiných trojúhelnících můžou být strany a úhly označeny jinak, ale podstata zůstane stále stejná. Můžete si to zapamatovat takto:
- Sinus je poměr délek protilehlé odvěsny ku přeponě.
- Kosinus je poměr délek přilehlé odvěsny ku přeponě.
- Tangens je poměr délek protilehlé odvěsny ku přilehlé.
- Kotangens je poměr délek přilehlé odvěsny ku protilehlé.
Ještě trochu to zjednodušíme, aby se vám to pamatovalo co nejlépe:
- Sinus – protilehlá ku přeponě.
- Kosinus – přilehlá ku přeponě.
- Tangens – protilehlá ku přilehlé.
- Kotangens – přilehlá ku protilehlé.
Přepišme si pro větší názornost tyto definice do zlomků:
\begin{align*}
\style{font-family: Arial, sans-serif;}{\text{sinus}} &= \frac{\style{font-family: Arial, sans-serif;}{\text{protilehlá}}}{\style{font-family: Arial, sans-serif;}{\text{přepona}}} \\ \\
\style{font-family: Arial, sans-serif;}{\text{kosinus}} &= \frac{\style{font-family: Arial, sans-serif;}{\text{přilehlá}}}{\style{font-family: Arial, sans-serif;}{\text{přepona}}} \\ \\
\style{font-family: Arial, sans-serif;}{\text{tangens}} &= \frac{\style{font-family: Arial, sans-serif;}{\text{protilehlá}}}{\style{font-family: Arial, sans-serif;}{\text{přilehlá}}} \\ \\
\style{font-family: Arial, sans-serif;}{\text{kotangens}} &= \frac{\style{font-family: Arial, sans-serif;}{\text{přilehlá}}}{\style{font-family: Arial, sans-serif;}{\text{protilehlá}}}
\end{align*}
Zde můžete vidět, že když si seřadíme všechny čtyři pojmy sinus, kosinus, tangens a kotangens v tomto pořadí pod sebe, tak se ve zlomcích opakuje určitý vzor:
- V čitatelích zlomků se střídají slova „protilehlá“ – „přilehlá“ – „protilehlá“ – „přilehlá“.
- To, co začíná na „ko“ (kosinus, kotangens), má v čitateli přilehlou odvěsnu, a co je bez „ko“ (sinus, tangens), má v čitateli protilehlou přeponu.
- Sinus a kosinus mají ve jmenovatelích přeponu a tangens a kotangens mají ve jmenovatelích opačnou odvěsnu než v čitatelích.
Snad vám tyto postřehy pomůžou si tyto poznatky lépe zapamatovat.
Ještě si připomeňme jednu věc: Pravoúhlý trojúhelník má dvě odvěsny a to, která z nich je protilehlá a která přilehlá, záleží na úhlu, kterým se zabýváme. Ukažme si náš obrázek pravoúhlého trojúhelníku ještě jednou:

Z hlediska úhlu $ \alpha $ je protilehlá odvěsna strana a a přilehlá odvěsna je strana b, ale z hlediska úhlu $ \beta $ je tomu přesně naopak – protilehlá odvěsna je strana b a přilehlá odvěsna je strana a.
Příklad
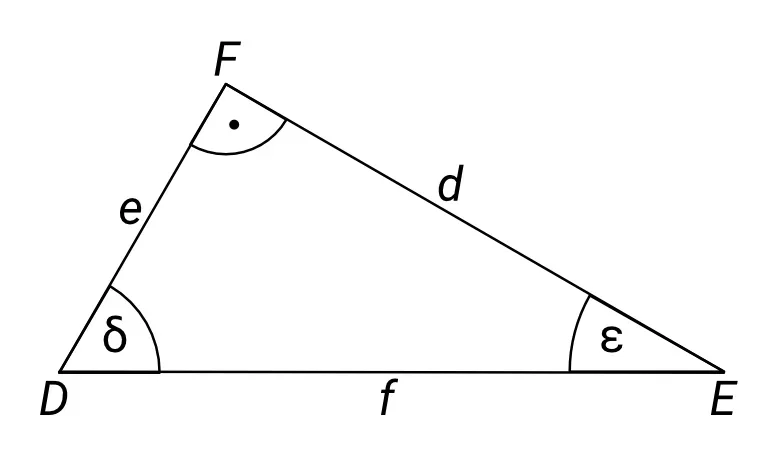
Zapište, čemu je roven sinus, kosinus, tangens a kotangens úhlů $ \delta $ (delta) a $ \epsilon $ (epsilon) v pravoúhlém trojúhelníku DEF na následujícím obrázku:
Řešení
V daném trojúhelníku je strana DE = f přepona, přilehlá odvěsna k úhlu $ \delta $ je strana DF = e, protilehlá odvěsna k úhlu $ \delta $ je strana EF = d, takže platí:
$$ \sin \delta = \frac{d}{f} $$
$$ \cos \delta = \frac{e}{f} $$
\[
\DeclareMathOperator{\tg}{tg} \\
\tg \delta = \frac{d}{e}
\]
\[
\DeclareMathOperator{\cotg}{cotg} \\
\cotg \delta = \frac{e}{d}
\]
V tomtéž trojúhelníku přilehlá odvěsna k úhlu $ \epsilon $ je strana EF = d, protilehlá odvěsna k úhlu $ \epsilon $ je strana DF = e, takže platí:
$$ \sin \epsilon = \frac{e}{f} $$
$$ \cos \epsilon = \frac{d}{f} $$
\[
\DeclareMathOperator{\tg}{tg} \\
\tg \epsilon = \frac{e}{d}
\]
\[
\DeclareMathOperator{\cotg}{cotg} \\
\cotg \epsilon = \frac{d}{e}
\]
Závěr
V tomto článku jsme si definovali pojmy sinus, kosinus, tangens a kotangens.
V následujícím článku si řekneme, že tyto pojmy jsou tzv. goniometrické funkce a spočítáme si jejich hodnoty pro vybrané velikosti úhlů, které budete potřebovat znát zpaměti.