Soustavy lineárních nerovnic

V předchozím článku jsme se věnovali lineárním nerovnicím.

V tomto článku na toto téma navážeme tím, že se podíváme na soustavy lineárních nerovnic. Budeme se zabývat soustavami lineárních nerovnic o jedné neznámé – nejedná se tedy o obdobu soustav dvou rovnic o dvou neznámých.

Vše si ukážeme na příkladech.

Příklad 1

Řešte soustavu nerovnic:

\begin{align*}
2x \; – \; 4 &\leqq 0 \\
3x + 3 &> 0
\end{align*}

Řešení

Vyřešíme každou nerovnici zvlášť:

\begin{align*} 2x \; – \; 4 &\leqq 0 \qquad |+4 \\ 2x &\leqq 4 \qquad |:2 \\ x &\leqq 2 \end{align*}

\begin{align*} 3x + 3 &> 0 \qquad |-3 \\ 3x &> -3 \qquad |:3 \\ x &> -1 \end{align*}

Výsledek první nerovnice $ x \leqq 2 $ odpovídá intervalu $ (-\infty; 2 \rangle $. Výsledek druhé nerovnice $ x > -1 $ odpovídá intervalu $ (-1; +\infty) $. Viz následující obrázek:

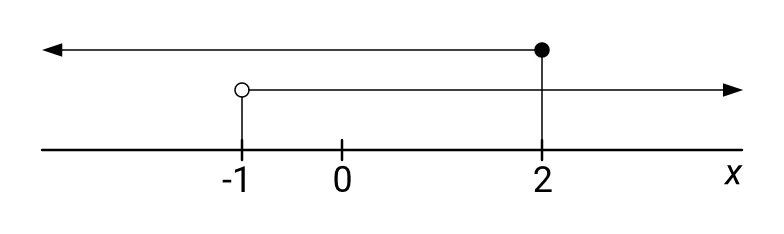
Řešením celé soustavy jsou ta čísla x, pro která platí současně $ x \leqq 2 $ a $ x > -1 $, tzn. která jsou menší nebo rovno 2 a současně větší než -1.

Množinově pak můžeme řešení zapsat takto: Označíme-li množinu řešení první nerovnice jako K₁ a množinu řešení druhé nerovnice jako K₂, pak množina řešení celé soustavy K bude průnikem množin K₁ a K₂:

\[ K = K_1 \cap K_2 = (-\infty; 2 \rangle \cap (-1; +\infty) = (-1; 2 \rangle \]

Z hlediska intervalů zakreslených na obrázku jsou to ta čísla, která leží pod oběma čarami vyznačujícími jednotlivé intervaly. Tento překrývající se úsek začíná zleva u čísla -1, přičemž u tohoto čísla máme prázdný kroužek, takže do výsledného intervalu ještě nepatří – v zápisu intervalu je proto na levé straně kulatá závorka, a končí u čísla 2, přičemž u tohoto čísla máme plný kroužek, takže do výsledného intervalu patří – v zápisu intervalu je proto na pravé straně lomená závorka.

Příklad 2

Řešte soustavu nerovnic:

\begin{align*}
2x \; – \; 4 &\geqq 0 \\
3x + 3 &< 0
\end{align*}

Řešení

Opět vyřešíme každou nerovnici zvlášť:

\begin{align*} 2x \; – \; 4 &\geqq 0 \qquad |+4 \\ 2x &\geqq 4 \qquad |:2 \\ x &\geqq 2 \end{align*}

\begin{align*} 3x + 3 &< 0 \qquad |-3 \\ 3x &< -3 \qquad |:3 \\ x &< -1 \end{align*}

Výsledek první nerovnice $ x \geqq 2 $ odpovídá intervalu $ \langle 2; +\infty) $. Výsledek druhé nerovnice $ x < -1 $ odpovídá intervalu $ (-\infty; -1) $. Viz následující obrázek:

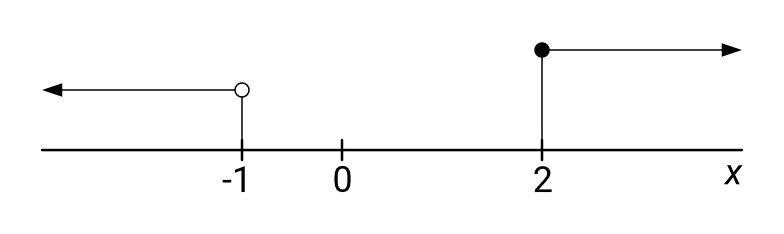
Řešením celé soustavy by měla být ta čísla x, pro která platí současně $ x \geqq 2 $ a $ x < -1 $, tzn. která jsou větší nebo rovno 2 a současně menší než -1. Ale žádná taková čísla neexistují, a proto soustava nerovnic nemá žádné řešení.

Je to podobné, jako kdybyste chtěli, aby venku byla teplota vyšší nebo rovno 2 °C a současně nižší než -1 °C – to prostě nejde. (Řešení předchozího příkladu by se dalo připodobnit k situaci, kdybyste chtěli, aby venku byla teplota nižší nebo rovno 2 °C a současně vyšší než -1 °C – taková teplota být klidně může.)

Intervaly zakreslené na obrázku se nikde nepřekrývají a nemůžou tudíž existovat čísla, které by ležela pod oběma čarami současně.

Množinově můžeme řešení zapsat takto:

\[ K = K_1 \cap K_2 = \langle 2; +\infty) \cap (-\infty; -1) = \emptyset \]

Příklad 3

Řešte soustavu nerovnic:

\begin{align*}
2x \; – \; 4 &\leqq 0 \\
3x + 3 &< 0
\end{align*}

Řešení

Vyřešíme každou nerovnici zvlášť:

\begin{align*} 2x \; – \; 4 &\leqq 0 \qquad |+4 \\ 2x &\leqq 4 \qquad |:2 \\ x &\leqq 2 \end{align*}

\begin{align*} 3x + 3 &< 0 \qquad |-3 \\ 3x &< -3 \qquad |:3 \\ x &< -1 \end{align*}

Výsledek první nerovnice $ x \leqq 2 $ odpovídá intervalu $ (-\infty; 2 \rangle $. Výsledek druhé nerovnice $ x > -1 $ odpovídá intervalu $ (-\infty; -1) $. Viz následující obrázek:

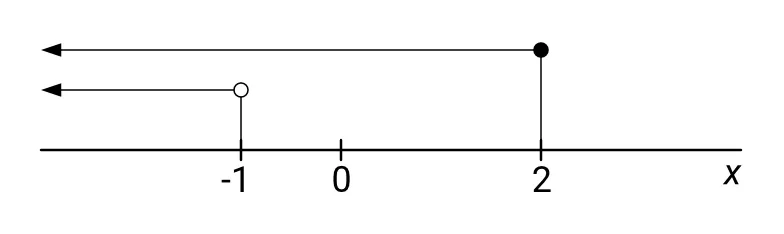
Řešení zapíšeme množinově:

\[ K = K_1 \cap K_2 = (-\infty; 2; \rangle \cap (-\infty; -1) = (-\infty; -1) \]

Intervaly zakreslené na obrázku se překrývají od čísla -1 do minus nekonečna, ale protože je zvykem psát menší hodnotu doleva a větší doprava, měli bychom spíš říct, že tyto intervaly se překrývají od minus nekonečna po číslo -1, přičemž samotné číslo -1 do průniku intervalů nepatří, protože u něj máme nakreslený prázdný kroužek.

Řešení lze opět připodobnit k situaci, kdybyste chtěli, aby venku byla teplota menší nebo rovno 2 °C a současně menší než -1 °C. Každá hodnota menší než -1 °C bude tomuto požadavku vyhovovat.

Probrali jsme si příklady, kdy řešením soustavy nerovnic byl buď konečný interval, nekonečný interval, nebo prázdná množina. Ukažme si na závěr příklad s trochu složitějším zadáním, kde navíc budeme mít soustavu tří nerovnic:

Příklad 4

Řešte soustavu nerovnic:

\begin{align*} 2(x \; – \; 0{,}4) &< 3{,}5x + 1{,}7 \\ 7x + \frac{1}{3} &> \frac{11}{15}(10x \; – \; 0{,}5) \\ \frac{x + 4}{8} &< 0{,}5 \; – \; \frac{3x \; – \; 5}{6} \end{align*}

Řešení

Opět nejdříve vyřešíme každou nerovnici zvlášť:

\begin{align*} 2(x \; – \; 0{,}4) &< 3{,}5x + 1{,}7 \qquad | \cdot 10 \\ 20(x \; – \; 0{,}4) &< 35x + 17 \\ 20x \; – \; 8 &< 35x + 17 \qquad |-35x + 8 \\ 20x \; – \; 35x &< 17 + 8 \\ -15x &< 25 \qquad |:(-15) \\ x &> -\frac{25}{15} \\ x &> -\frac{5}{3} \end{align*}

Všimněte si, že ke konci výpočtu jsme museli otočit znak nerovnosti z < na >, protože jsme nerovnici dělili záporným číslem.

\begin{align*} 7x + \frac{1}{3} &> \frac{11}{15}(10x \; – \; 0{,}5) \qquad | \cdot 15 \\ 105x + 5 &> 11(10x \; – \; 0{,}5) \\ 105x + 5 &> 110x \; – \; 5{,}5 \qquad | \cdot 2 \\ 210x + 10 &> 220x \; – \; 11 \qquad |-220x \; – \; 10 \\ 210x \; – \; 220x &> -11 \; – \; 10 \\ -10x &> -21 \qquad |:(-10) \\ x &< \frac{21}{10} \end{align*}

I zde jsme museli ke konci výpočtu otočit znak nerovnosti, tentokrát z > na <, protože jsme rovnici dělili záporným číslem.

\begin{align*} \frac{x + 4}{8} &< 0{,}5 \; – \; \frac{3x \; – \; 5}{6} \qquad | \cdot 24 \\ 3(x + 4) &< 12 \; – \; 4(3x \; – \; 5) \\ 3x + 12 &< 12 \; – \; 12x + 20 \\ 3x + 12 &< 32 \; – \; 12x \qquad |+12x \; – \; 12 \\ 3x + 12x &< 32 \; – \; 12 \\ 15x &< 20 \qquad |:15 \\ x &< \frac{20}{15} \\ x &< \frac{4}{3} \end{align*}

Jednotlivá dílčí řešení můžeme zapsat množinově pomocí intervalů takto:

$$ K_1 = \bigg({-}\frac{5}{3}; +\infty\bigg) $$

$$ K_2 = \bigg({-}\infty; \frac{21}{10}\bigg) $$

$$ K_3 = \bigg({-}\infty; \frac{4}{3}\bigg) $$

Celkové řešení bude tvořit průnik všech těchto tří intervalů. Abychom se v tom lépe vyznali, vyznačíme si jednotlivé intervaly na číselnou osu, na kterou si nejprve vyneseme obrazy čísel, jež tvoří hranice těchto intervalů.

Nezáleží na tom, aby byly obrazy těchto čísel zakreslené přesně, důležité je pouze je správně uspořádat podle velikosti. Číslo $ -\frac{5}{3} $ je nejmenší, protože je jediné záporné, takže jeho obraz na číselné ose bude nejvíc vlevo, číslo $ \frac{21}{10} $ je něco málo přes 2, což je víc než $ \frac{4}{3} $, které jsou někde mezi čísly 1 a 2, takže bude nejvíc vpravo, a číslo $ \frac{4}{3} $ bude tím pádem někde uprostřed.

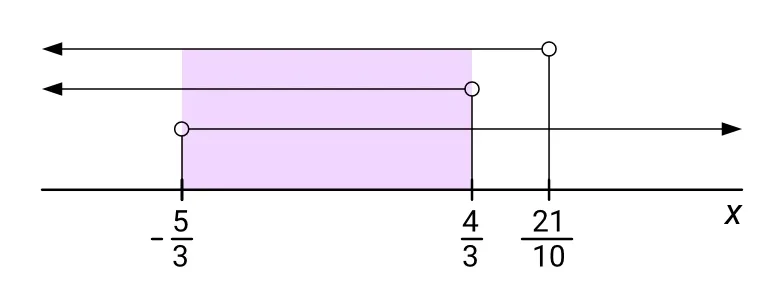
Do celkového řešení budou patřit všechna čísla, která leží pod všemi třemi čarami vyznačujícími jednotlivé intervaly. Na obrázku je tento úsek zvýrazněn světle fialovou barvou. Můžeme tedy zapsat množinu K kořenů soustavy nerovnic:

\[ K = K_1 \cap K_2 \cap K_3 = \bigg({-}\frac{5}{3}; \frac{4}{3}\bigg) \]

Závěr

V tomto článku jsme probrali soustavy lineárních nerovnic. Mnohé z těchto poznatků se nám budou ještě hodit u nerovnic v součinovém nebo podílovém tvaru a také u nerovnic s absolutními hodnotami.

V následujícím článku se podíváme na nerovnice v součinovém tvaru.