Souřadnice v prostoru

V předchozím článku jsme se zabývali souřadnicemi v rovině.

V tomto článku tento pojem rozšíříme o další rozměr, čímž dostaneme souřadnice v prostoru.

Definice kartézského systému souřadnic v prostoru

Souřadnice v prostoru můžeme definovat podobně, jako jsme definovali souřadnice v rovině:

Kartézská soustava souřadnic je ve volném rovnoběžném promítání zobrazena na následujícím obrázku:

Vidíme, že osy x a y leží jakoby v rovině a osa z směřuje do výšky. Záporné poloosy jsou vykresleny čárkovanými čarami.

Je to podobné jako na Zemi, když zanedbáme její kulatost. Představte si například nějaké město obklopené horami. Počátek kartézské soustavy souřadnic bychom mohli umístit do středu tohoto města. Pro jednoduchost předpokládejme, že nadmořská výška tohoto středu města je nulová. Potom bychom mohli definovat kartézský souřadný systém například tak, že kladná poloosa x bude by odpovídala východnímu směru, záporná poloosa x západnímu směru, kladná poloosa y severnímu směru a záporná poloosa y jižnímu směru.

Souřadnice x nějakého místa by pak odpovídala vzdálenosti tohoto místa od středu města směrem na východ nebo na západ, a souřadnice y pak vzdálenosti směrem na sever nebo na jih. Pokud byste ale vyjeli do okolních hor, pak byste k přesnému určení místa potřebovali ještě třetí souřadnici, a sice nadmořskou výšku, které by odpovídala souřadnice z. Viz následující ilustrační obrázek:

Kdybyste byli od středu města vzdáleni třeba 5 kilometrů na východ a 10 kilometrů na sever, a současně byste byli v nadmořské výšce např. 1,2 kilometru, pak byste mohli udat svoji polohu jako trojici uspořádaných čísel [x; y; z], která by v tomto případě byla [5; 10; 1,2]. Pokud byste byly vzdáleni od středu města např. 7 kilometrů na západ, 3 kilometry na jih a v nadmořské výšce 0,6 km, tak byste mohli udat svoji polohu jako [-7; -3; 0,6].

Souřadnice bodu v prostoru

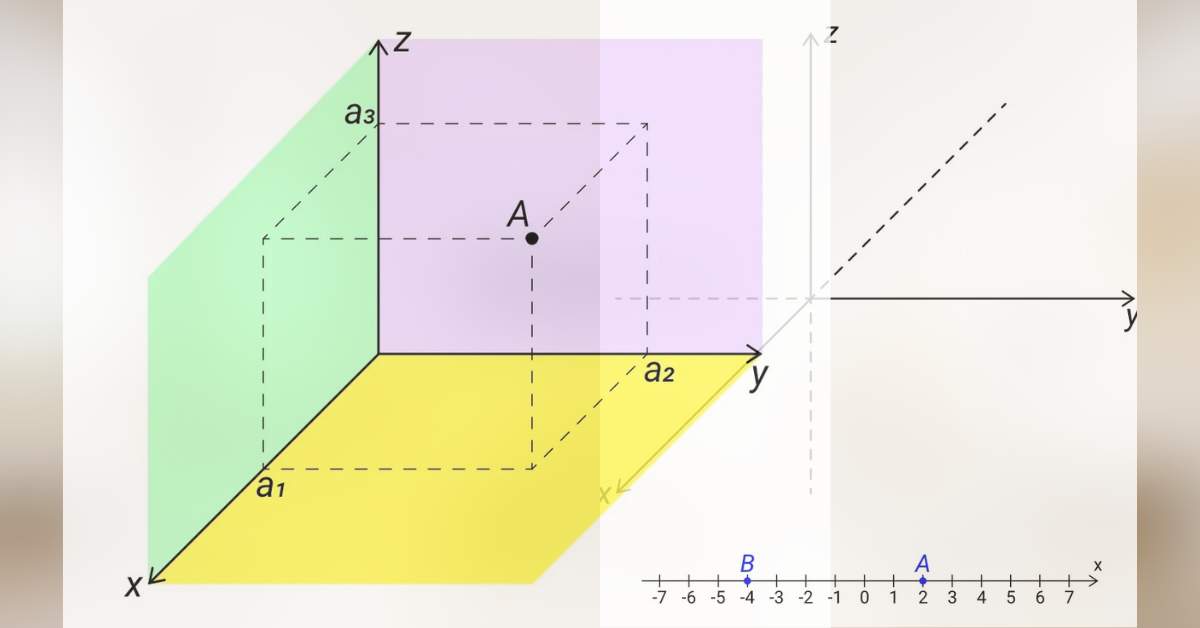
Nyní si řekneme, jak můžeme získat souřadnice bodu v prostoru – viz následující obrázek:

Máme-li v prostoru libovolný bod A, můžeme jím vést roviny rovnoběžné se souřadnicovými rovinami (barevné plochy na obrázku):

• Rovina procházející bodem A a rovnoběžná s rovinou yz kartézského systému souřadnic (fialová plocha na obrázku) protne osu x v čísle, které označíme jako a₁.
• Rovina procházející bodem A a rovnoběžná s rovinou xz kartézského systému souřadnic (zelená plocha na obrázku) protne osu y v čísle, které označíme jako a₂.
• Rovina procházející bodem A a rovnoběžná s rovinou xy kartézského systému souřadnic (žlutá plocha na obrázku) protne osu z v čísle, které označíme jako a₃.

Čísla a₁, a₂, a₃ se nazývají souřadnice bodu A. Podobně jako v rovině, má-li bod A souřadnice a₁, a₂, a₃, zapisujeme A[a₁; a₂; a₃]. Dolní index 1 tedy odpovídá x-ové souřadnici bodu, dolní index 2 y-ové souřadnici bodu, a dolní index 3 z-ové souřadnici bodu.

Pouze z obrázku ovšem nemůžeme určit polohu každého bodu jednoznačně, protože tento obrázek je pouze dvourozměrný, zatímco prostor třírozměrný, takže různé body v prostoru by nám mohly na obrázku splynout do bodu jednoho.

Na závěr si ukážeme jeden příklad, ve kterém zakreslíme bod v prostoru o daných souřadnicích do kartézské soustavy souřadnic.

Příklad

Zakreslete do kartézské soustavy souřadnic bod A[6; 4; 3].

Řešení

V kartézské soustavě souřadnic si zvolíme nějakou jednotku, podle které si očíslujeme osy. (Osa x je nakreslená v rovnoběžném promítání směrem „dopředu“, takže na ní nakreslíme tyto jednotky např. o poloviční velikosti než na osách y a z.)

Dále si sestrojíme pomocné body A₁, A₂, A₃:

• V čísle 6 na ose x nakreslíme rovnoběžku s osou y a v čísle 4 na ose y nakreslíme rovnoběžku s osou x. Tyto rovnoběžky se protnou v pomocném bodě A₁.
• V čísle 6 na ose x nakreslíme rovnoběžku s osou z a v čísle 3 na ose z nakreslíme rovnoběžku s osou x. Tyto rovnoběžky se protnou v pomocném bodě A₂.
• V čísle 4 na ose y nakreslíme rovnoběžku s osou z a v čísle 3 na ose z nakreslíme rovnoběžku s osou y. Tyto rovnoběžky se protnou v pomocném bodě A₃.

Dále z těchto pomocných bodů A₁, A₂, A₃ nakreslíme rovnoběžky po řadě se souřadnicovými osami z, y, x. Tyto rovnoběžky se protnou v bodě A.

Celou konstrukci zachycuje následující obrázek:

Ještě připomeňme, že kartézskou soustavu souřadnic – ať už v rovině nebo prostoru – budeme používat v celé analytické geometrii, přičemž často budeme psát pouze „soustava souřadnic“ nebo „souřadný systém“.

Závěr

V tomto článku jsme si popsali kartézskou soustavu souřadnic v prostoru.

V následujícím článku se budeme věnovat vzdálenostem bodů.