Sčítání vektorů

V předchozím článku jsme si vysvětlili, co je to vektor, jaké vektory používáme v analytické geometrii, a jak se stanovují souřadnice vektorů.

V tomto článku se začneme věnovat aritmetickým operacím s vektory, z nichž první je sčítání vektorů.

Působí-li na těleso dvě síly, můžeme tyto síly složit a nahradit je jedinou silou, jejíž působení má stejný výsledek. Vektory se sčítají tak, aby jejich součet odpovídal skládání sil.

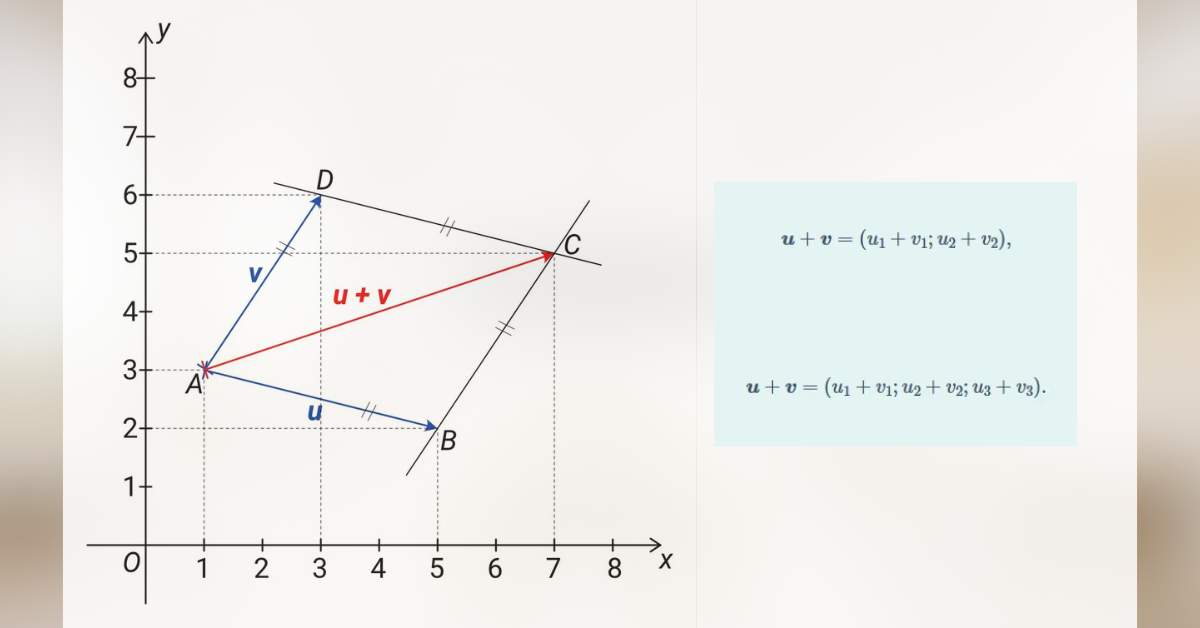
Geometricky můžeme dva vektory sečíst doplněním na rovnoběžník. Nakreslíme si vektory tak, aby měly počátek ve stejném bodě, potom bodem odpovídajícím konci prvního vektoru vedeme rovnoběžku s druhým vektorem a bodem odpovídajícím konci druhého vektoru vedeme rovnoběžku s prvním vektorem. Výsledný vektor pak bude směřovat z počátečního bodu do bodu, ve kterém se protínají rovnoběžky – viz následující obrázek:

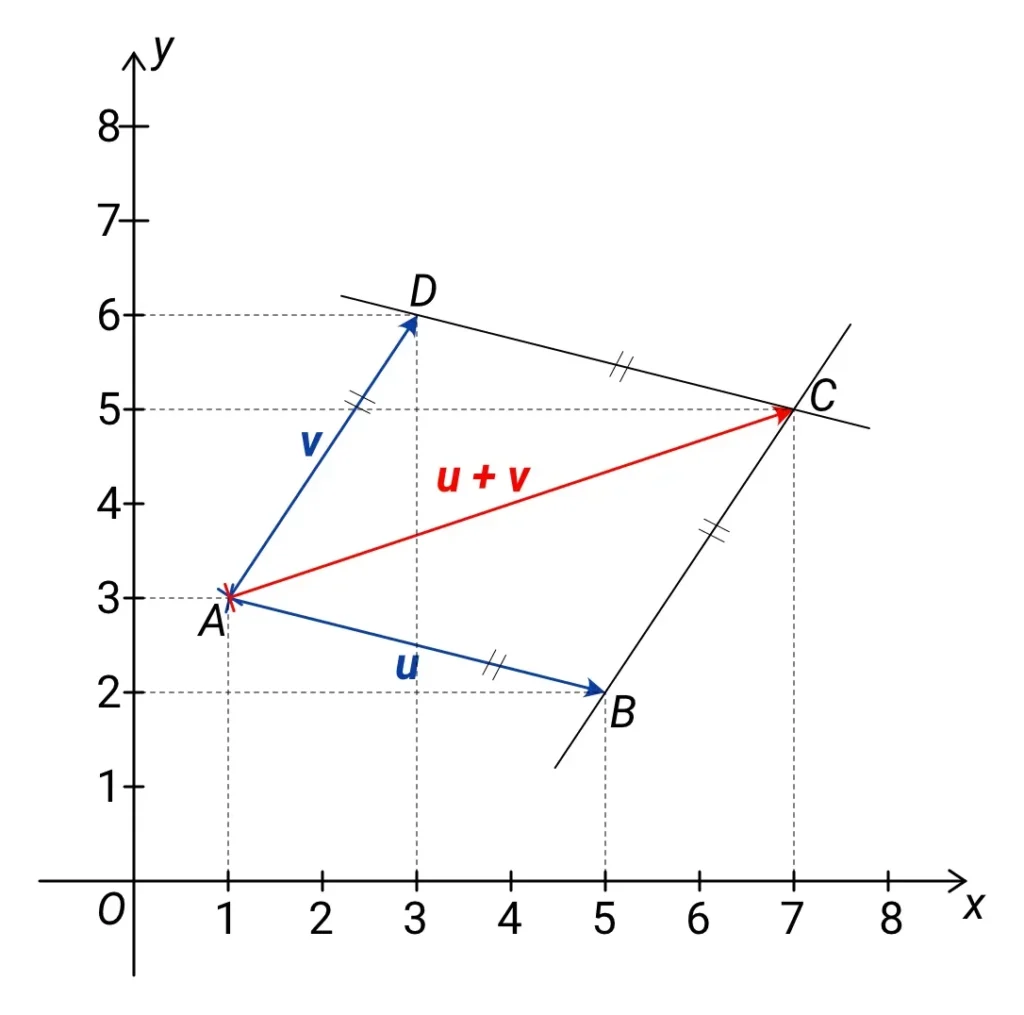
Na obrázku máme rovnoběžník ABCD, kde bod A je počátečním bodem vektorů u a v, které sčítáme, bod B odpovídá konci vektoru u, bod D konci vektoru v a orientovaná úsečka AC pak odpovídá výsledku součtu těchto vektorů. Tato orientovaná úsečka tvoří úhlopříčku rovnoběžníku ABCD.

Druhý způsob, jak můžeme geometricky sečíst dva vektory, je takový, že druhý vektor nakreslíme tak, aby měl počátek na konci prvního vektoru. Výsledný vektor pak bude tvořen orientovanou úsečkou, směřující z bodu, který odpovídá začátku prvního vektoru, do bodu, který odpovídá konci druhého vektoru – viz následující obrázek:

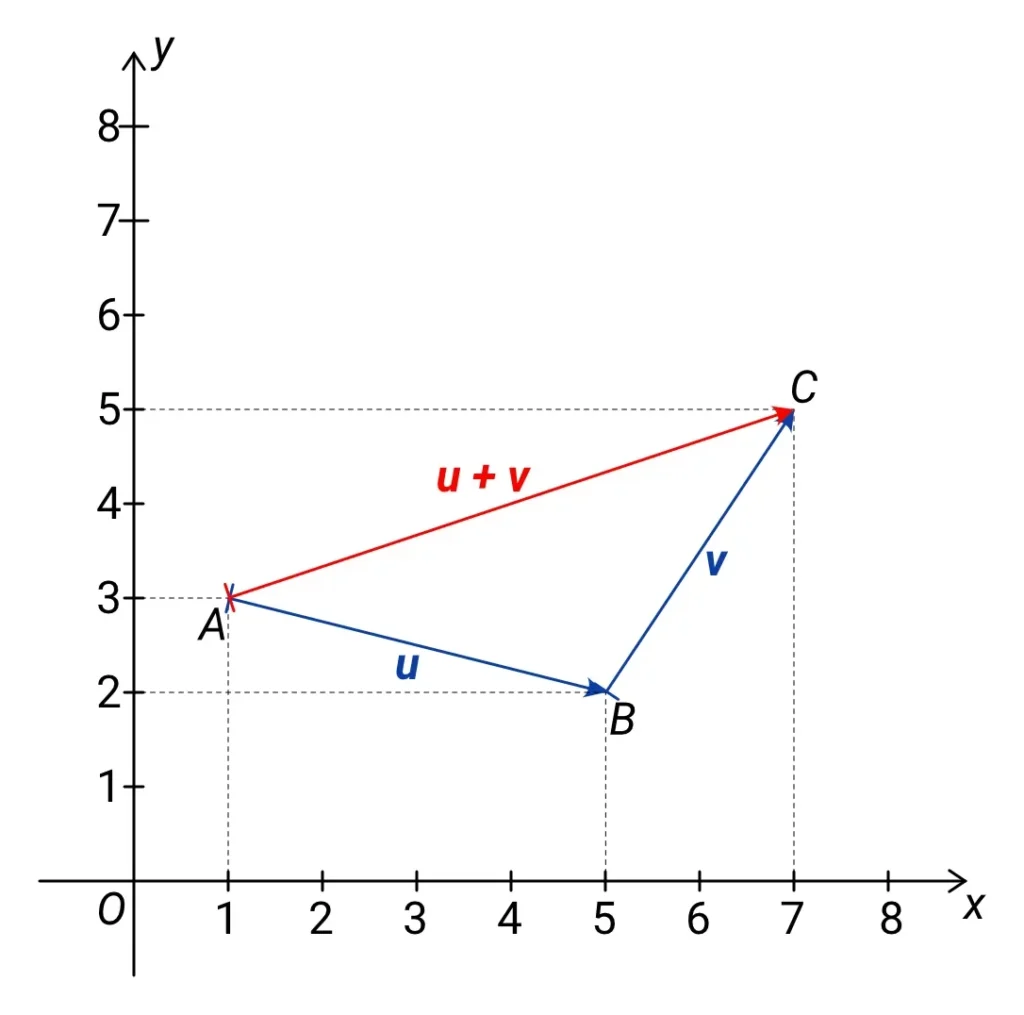
Na základě tohoto obrázku můžeme vyslovit definici součtu vektorů:

Součet vektorů u = B – A, v = C – B, je vektor C – A. Zapisujeme u + v = C – A.

Tento způsob má výhodu, že pomocí něj můžeme sečíst i více než dva vektory najednou – viz následující obrázek:

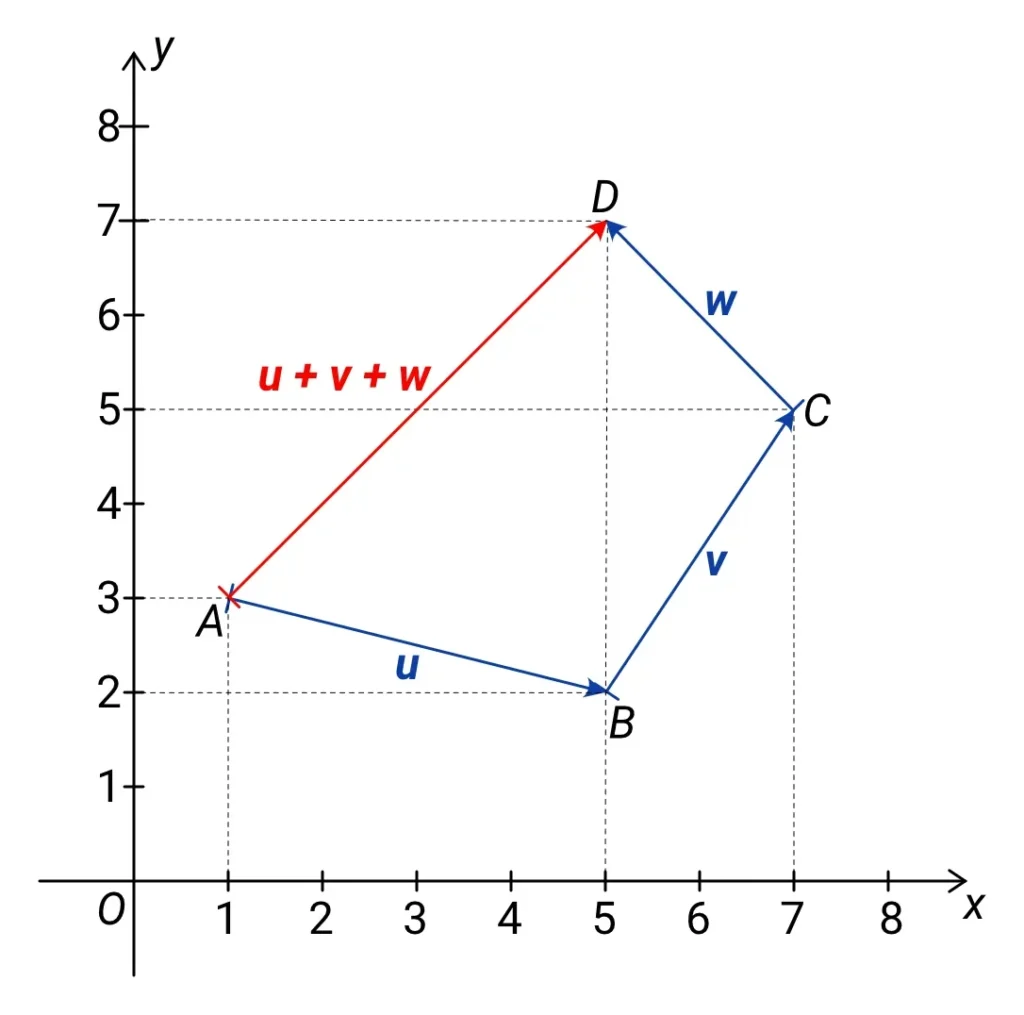
Zde sčítáme vektory u + v + w tak, že je zřetězíme, tzn. začátek každého dalšího umístíme na konec předchozího. Výsledný vektor pak získáme tak, že spojíme orientovanou úsečkou začátek prvního vektoru s koncem posledního.

Matematicky sečteme vektory tak, že sečteme zvlášť jejich x-ové a y-ové souřadnice (v prostoru ještě z-ové souřadnice). Matematická definice součtu je tedy následující:

O této definici se můžeme přesvědčit z obrázku 2: souřadnice vektorů na něm jsou u = (4; –1), v = (2; 3) a u + v = (4 + 2; –1 + 3) = (6; 2). Když se podíváme na výsledný vektor u + v, vidíme, že abychom se dostali z jeho začátku (bod A) na jeho konec (bod C), musíme se ve směru osy x skutečně posunout o 6 jednotek a ve směru osy y o 2 jednotky. Nebo si můžeme souřadnice tohoto výsledného vektoru spočítat jako rozdíl bodů C – A:

\begin{align*} u_1 = c_1 -a_1 = 7 -1 = 6 \\ u_2 = c_2 -a_2 = 5 -3 = 2 \end{align*}

Sčítání vektorů je komutativní, což znamená, že nezáleží na pořadí vektorů, které sčítáme. To je patrné i z obrázku 1.

Odčítání vektorů

Odčítání obecně je v podstatě druhem sčítání. Chceme-li odečíst např. od čísla 5 číslo 3, můžeme to udělat tak, že k číslu 5 přičteme číslo opačné k číslu 3, což je -3:

$$ 5 -3 = 5+(-3) = 2 $$

Zároveň platí, že sečteme-li dvě opačná čísla, např. 4 a -4, výsledek bude nula.

S vektory je to obdobné. Uveďme nejprve definici nulového a opačného vektoru:

Vektor určený nulovou orientovanou úsečkou se nazývá nulový vektor a označuje se o. Je-li u = B – A, nazývá se vektor A – B opačný vektor k vektoru u a označuje se –u.

Pro každý vektor u platí u + o = u a u + (–u) = o.

Odčítání vektorů znázorňuje následující obrázek, kde od vektoru u odčítáme vektor v:

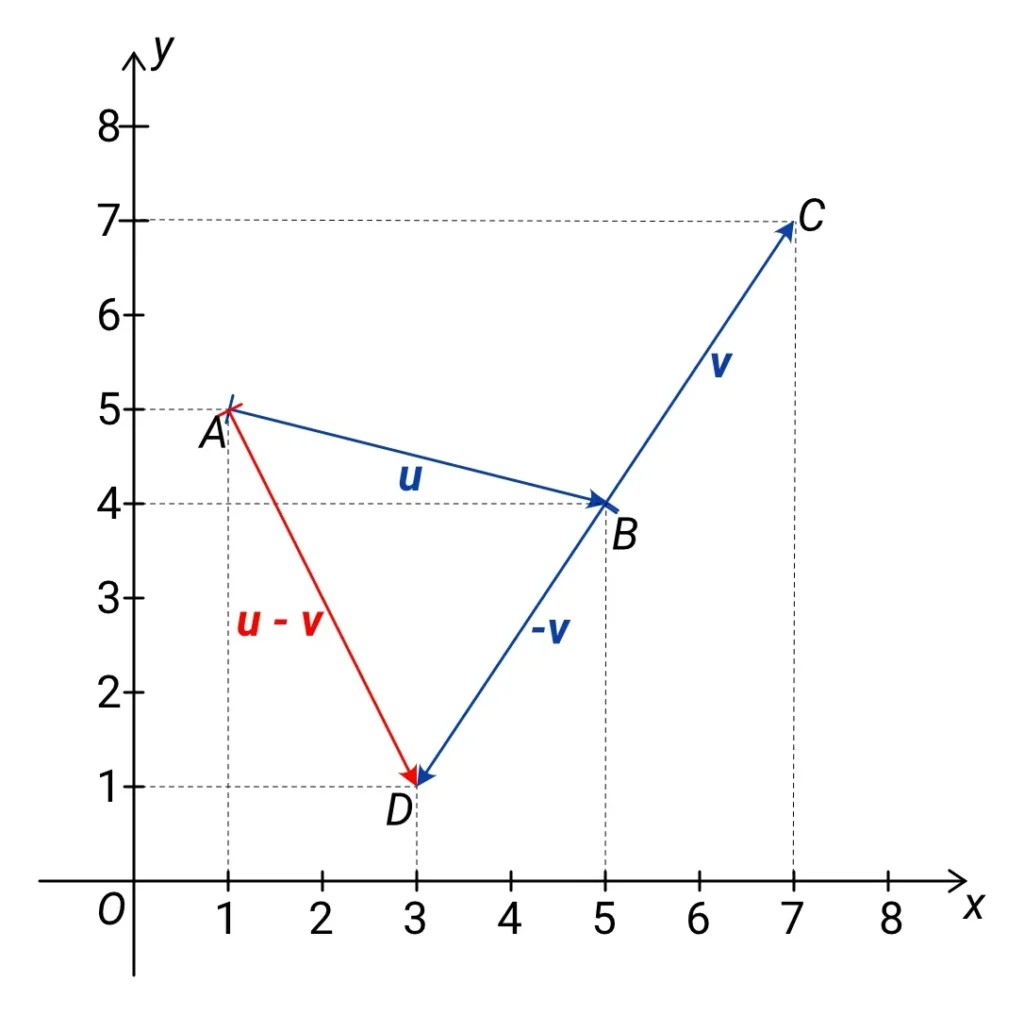
Vidíme, že jsme si sestrojili vektor opačný k vektoru v tak, že jsme zachovali jeho délku a otočili jsme ho do opačného směru. Následně tento opačný vektor přičítáme k vektoru u. Souřadnice opačného vektoru mají opačná znaménka než souřadnice původního vektoru.

V rovině tedy platí:

\[ \boldsymbol{u} = (u_1; u_2) \implies -\boldsymbol{u} = (-u_1; -u_2) \]

a podobně v prostoru:

\[ \boldsymbol{u} = (u_1; u_2; u_3) \implies -\boldsymbol{u} = (-u_1; -u_2; -u_3) \]

Vektor v na obrázku má souřadnice v = (2; 3), takže vektor –v musí mít souřadnice –v = (-2; -3). Snadno se z obrázku můžete přesvědčit, že je tomu skutečně tak.

Vektor v tedy odečteme od vektoru u tak, že k vektoru u přičteme vektor opačný k vektoru v.

Matematicky odečteme vektory tak, že od souřadnic prvního vektoru odečteme souřadnice druhého vektoru:

Geometricky můžeme dva vektory odečíst také tak, že si oba vektory nakreslíme s počátkem ve stejném bodě, a sestrojíme orientovanou úsečku z konce odčítaného vektoru po konec vektoru, od kterého odčítáme – viz následující obrázek:

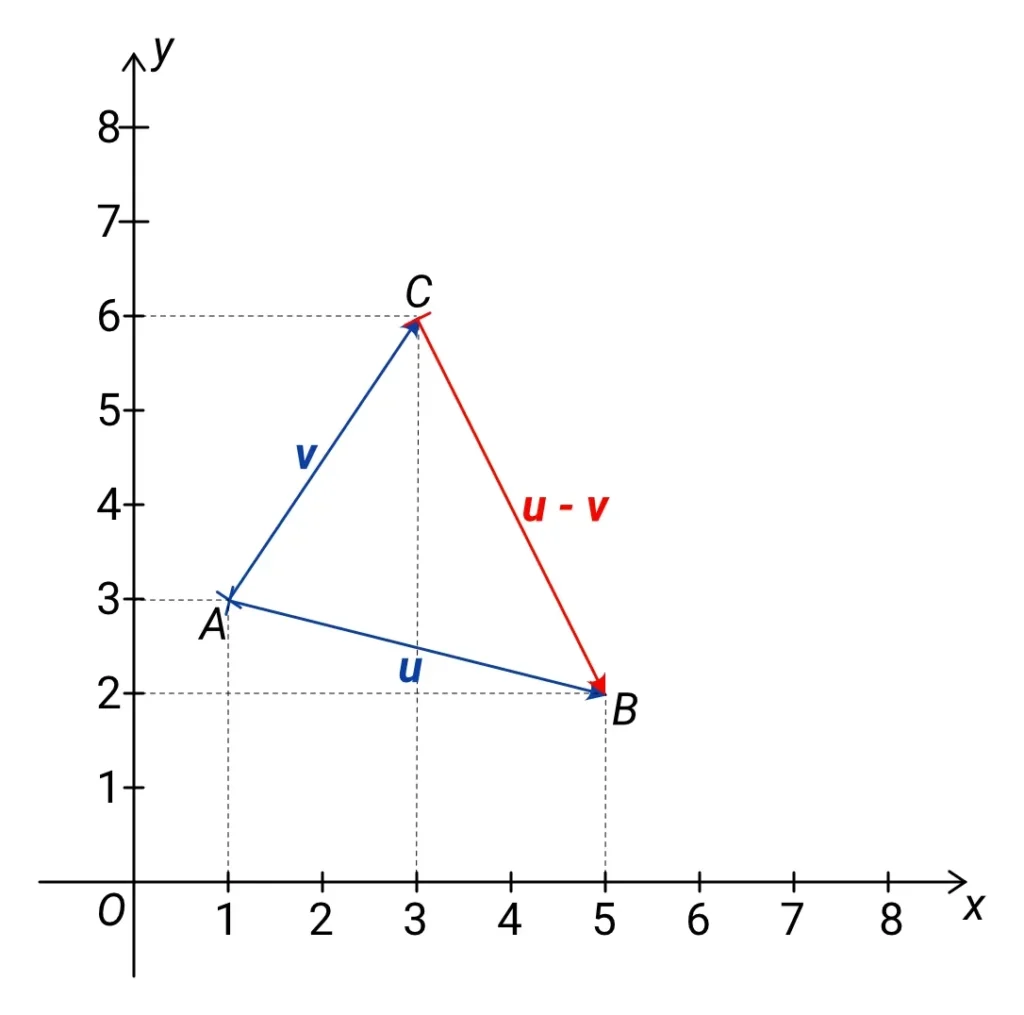
Na závěr si ukážeme aspoň jeden příklad:

Příklad

V prostoru jsou dány vektory u = (1; -3; 2), v = (2; 1; -4). Vypočítejte jejich součet a rozdíl.

Řešení

\begin{align*} \boldsymbol{u} + \boldsymbol{v} &= (u_1 + v_1; u_2 + v_2; u_3 + v_3) \\ &= (1 + 2; -3 + 1; 2 + (-4) = (3; -2; -2) \end{align*}

\begin{align*} \boldsymbol{u} -\boldsymbol{v} &= (u_1 -v_1; u_2 -v_2; u_3 -v_3) \\ &= (1 -2; -3 -1; 2 -(-4) = (-1; -4; 6) \end{align*}

Závěr

V tomto článku jsme probrali sčítání a odčítání vektorů, které matematicky můžeme provést tak, že sečteme, resp. odečteme, příslušné souřadnice sčítaných, resp. odčítaných, vektorů.

V následujícím článku se budeme věnovat násobení vektoru reálným číslem.