V předchozím článku jsme si probrali Pythagorovu větu a ukázali si její použití při výpočtech délek stran pravoúhlého trojúhelníku.
Pythagorova věta se však velmi často vyskytuje v nejrůznějších geometrických i jiných úlohách, kde nemusí být na první pohled zřejmé, že ji lze použít, nebo kde onen pravoúhlý trojúhelník hledat. Proto si v tomto článku ukážeme ještě několik takových příkladů.
Příklad 1
Vypočítejte úhlopříčku obdélníku se stranami délek 10 metrů a 5 metrů.
Řešení
Nakreslíme si obrázek:

Označíme-li si delší stranu obdélníku jako a, kratší stranu jako b a úhlopříčku jako u, pak platí:
\begin{align*} u &= \sqrt{a^2 + b^2} = \sqrt{10^2 + 5^2} = \\ &= \sqrt{100 + 25} = \sqrt{125} \doteq 11{,}18 \text{ m} \end{align*}
Příklad 2
O stěnu je opřený žebřík, který stojí na vodorovném terénu. Výška žebříku je 13 metrů a vzdálenost paty žebříku od stěny je 5 metrů. Do jaké výšky sahá žebřík?
Řešení
Nakreslíme si obrázek:

Stěna je kolmá na vodorovný terén, takže spolu s žebříkem máme pravoúhlý trojúhelník a můžeme použít Pythagorovu větu. Tentokrát známe délku přepony, což je délka žebříku, a budeme počítat délku odvěsny – výšku, do které žebřík sahá. Budeme tedy od čtverce nad přeponou odčítat čtverec nad známou odvěsnou, což je vzdálenost paty žebříku od stěny:
\begin{align*}
v &= \sqrt{13^2 \; – \; 5^2} = \sqrt{169 \; – \; 25 } = \\
&= \sqrt{144} = 12 \text{ m}
\end{align*}
Příklad 3
Vypočítejte výšku dopadající na základnu rovnostranného trojúhelníku ABC, jestliže tato základna má délku z = 8 cm a jeho ramena mají délku r = 9 cm.
Řešení
Nakreslíme si obrázek:
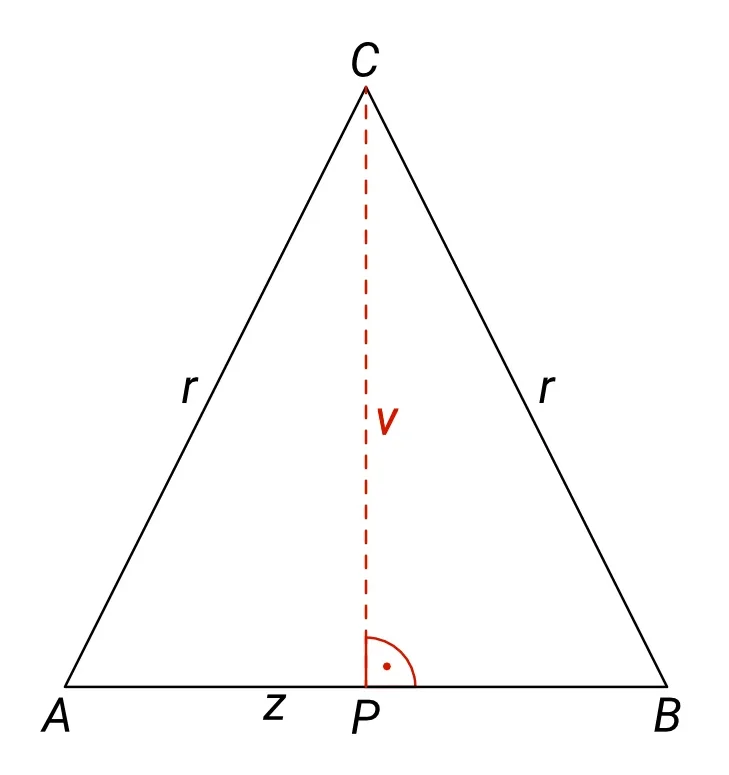
Rovnostranný trojúhelník je osově souměrný (symetrický) právě podle osy, na níž leží výška, která dopadá na jeho základnu. To znamená, že spustíme-li výšku z bodu C, tak tato výška rozdělí rovnostranný trojúhelník na dva shodné pravoúhlé trojúhelníky, v našem případě trojúhelníky BCP a APC.
Zároveň platí, že bod P, kam tato výška dopadne, rozdělí základnu přesně na dvě poloviny, takže jedna z odvěsen těchto pravoúhlých trojúhelníků bude mít poloviční délku než celá základna z.
Jelikož jsme tímto rozdělením získali pravoúhlé trojúhelníky, můžeme použít Pythagorovu větu. V našem případě platí, že čtverec nad výškou je rozdílem čtverce nad přeponou r a čtverce nad polovinou základny, např. nad úsečkou PB.
Platí tedy:
\begin{align*}
v &= \sqrt{r^2 \; – \; \bigg(\frac{z}{2}\bigg)^2} = \sqrt{9^2 \; – \; 4^2} = \\
&= \sqrt{81 \; – \; 16} = \sqrt{65} \doteq 8{,}06 \text{ cm}
\end{align*}
Příklad 4
Je dán rovnoramenný lichoběžník ABCD, se základnami délek a = 20 cm, c = 8 cm, a rameny b = d = 12 cm. Vypočtěte jeho obsah.
Řešení
Nakreslíme si obrázek:
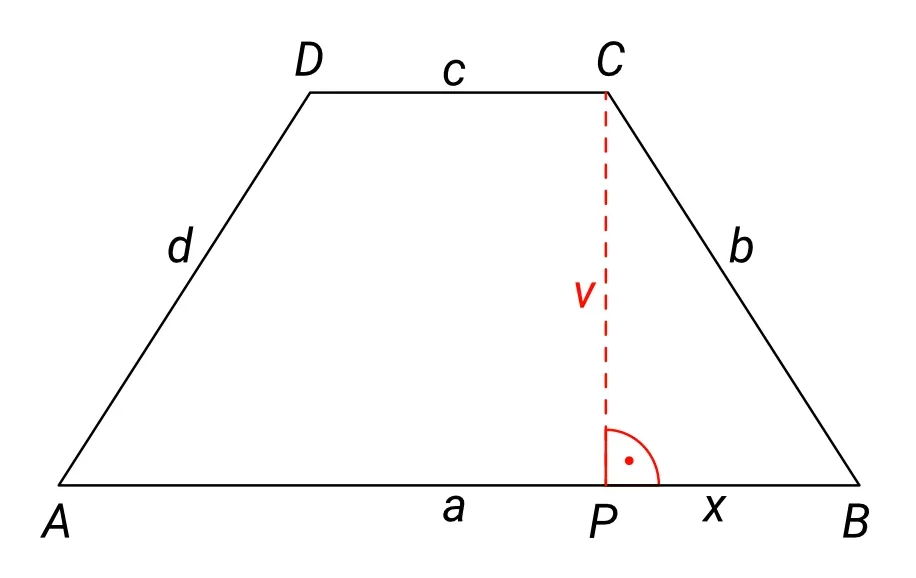
Obsah lichoběžníku spočítáme tak, že zprůměrujeme jeho základny a tento mezivýsledek vynásobíme jeho výškou, tedy podle vzorce:
$$ S = \frac{a + c}{2} \cdot v $$
My máme zadány délky obou základen, ale neznáme výšku. Proto si ji potřebujeme nějak dopočítat. Když si tuto výšku nakreslíme tak, aby vycházela z bodu C, tak dopadne na stranu a pod pravým úhlem (výška vždycky dopadá na danou stranu pod pravým úhlem) a zároveň nám vytvoří pravoúhlý trojúhelník se stranami, které jsou v obrázku označeny jako x, b, v.
Potřebujeme znát dvě ze stran pravoúhlého trojúhelníku, abychom si pomocí Pythagorovy věty mohli spočítat stranu třetí, ale my neznáme ani výšku v, ani stranu x. Známe pouze délku strany b a to samozřejmě nestačí. Takže si nejdřív musíme nějak spočítat délku strany x.
Základny lichoběžníku a a c jsou rovnoběžné a lichoběžník je navíc rovnoramenný, což znamená, že kdybychom si nakreslili jeho osu, byl by podle ní osově souměrný. Z toho vyplývá, že kdybychom si nakreslili výšku na levou stranu místo na pravou, tedy tak aby vycházela z bodu D, tak úsek x na levé straně lichoběžníku by byl stejně dlouhý jako je na straně pravé.
Kdybychom dále oba tyto úseky x ze spodní základny a odstranili, zbyla by nám úsečky o délce strany c. Podívejte se na následující obrázek, který celou situaci znázorňuje:
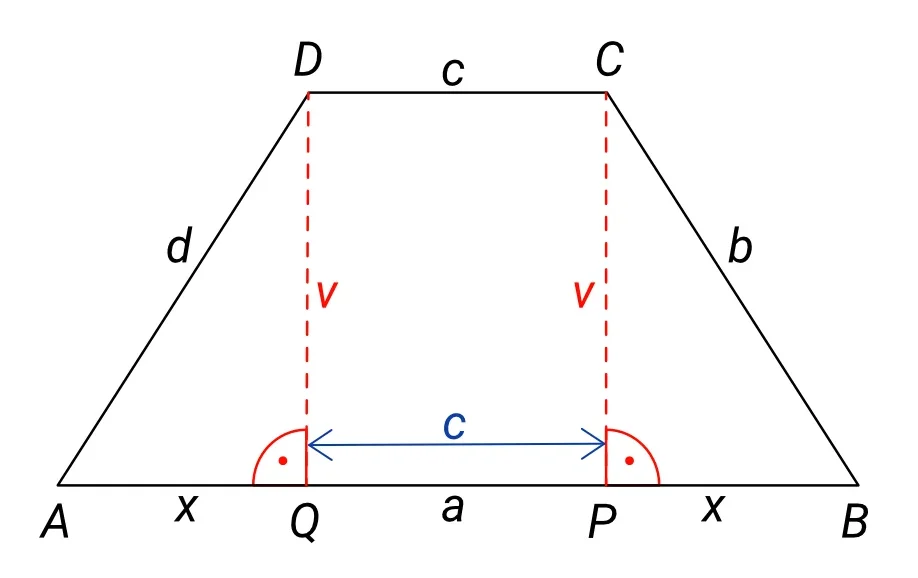
Geometrický útvar QPCD je totiž obdélník, a obdélník má protilehlé strany vždy stejně dlouhé.
Z obrázku tedy vidíme, že spodní základna lichoběžníku a se skládá z úsečky x, dále z úsečky o délce strany c, a nakonec opět z úsečky x, takže platí:
$$ a = x + c + x \text{ , tedy } a = 2x + c $$
Délky stran a a c máme zadány, takže si můžeme spočítat délku úsečky x jejich dosazením do právě uvedeného vztahu:
\begin{align*}
a &= 2x + c \\
20 &= 2x + 8 \qquad |- \; 8 \\
12 &= 2x \qquad |:2 \\
x &= 6 \text{ cm}
\end{align*}
Jinými slovy, když od délky strany a odečteme délku stranu c, dostaneme celkovou délku dvou úseček x, takže toto číslo vydělíme dvěma a máme délku jedné úsečky x: $ 20 \; – \; 8 = 12 $ a $ 12:2 = 6 \text{ cm}$.
Teď už nám nic nebrání spočítat si pomocí Pythagorovy věty výšku lichoběžníku:
\begin{align*} v &= \sqrt{b^2 \; – \; x^2} = \sqrt{12^2 \; – \; 6^2} = \\ &= \sqrt{144 \; – \; 36} = \sqrt{108} \doteq 10{,}39 \text{ cm} \end{align*}
Tuto výšku nyní můžeme dosadit do vzorce pro výpočet obsahu lichoběžníku a získat tak výsledek celého příkladu:
\begin{align*} S &= \frac{a + c}{2} \cdot v = \frac{20 + 8}{2} \cdot 10{,}39 \\ &= \frac{28}{2} \cdot 10{,}39 = 14 \cdot 10{,}39 = 145{,}46 \text { cm}^2 \\ \end{align*}
Příklad 5
Z křižovatky kolmých silnic vyjeli ve stejném okamžiku dva cyklisté. Cyklista A po jedné silnici rychlostí 20 km/h a cyklista B pro druhé silnici rychlostí 24 km/h. Jaká bude jejich vzájemná vzdálenost po třiceti minutách?
Řešení
Ze všeho nejdříve si převedeme čas 30 minut na hodiny, abychom v příkladu měli konzistentní jednotky, protože rychlost obou cyklistů je zadána v kilometrech za hodinu.
$$ 30 \text{ min } = \frac{1}{2} \text{ h} $$
Uražená dráha při rovnoměrném pohybu se spočítá jako čas krát rychlost. Cyklista A tedy ujede za třicet minut dráhu:
$$ s_1 = 20 \cdot \frac{1}{2} = 10 \text{ km} $$
Cyklista B ujede za třicet minut dráhu:
$$ s_2 = 24 \cdot \frac{1}{2} = 12 \text{ km} $$
Celou situaci po třiceti minutách ukazuje následující obrázek:
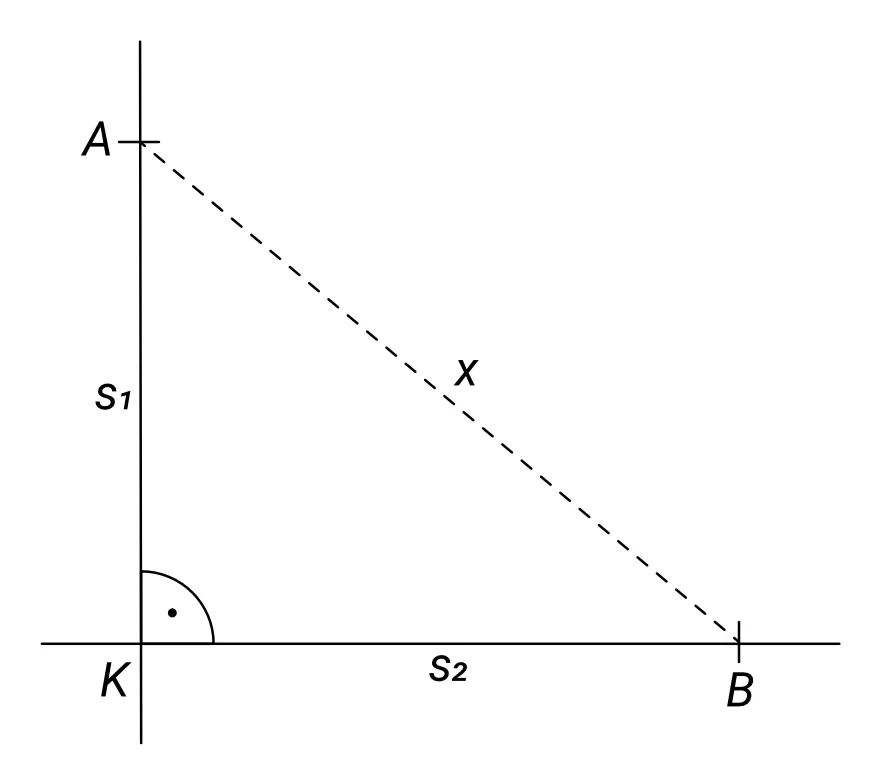
Svislá a vodorovná čára představují kolmé silnice, bod K je křižovatka, ze které cyklisté vyjeli, a body A, B jsou jejich aktuální polohy. Jejich vzájemnou vzdálenost reprezentuje přerušovaná čára x. Tuto vzdálenost určíme z Pythagorovy věty:
$$ x^2 = s_1^2 + s_2^2 $$
neboli:
\begin{align*} x &= \sqrt{s_1^2 + s_2^2} = \sqrt{10^2 + 12^2} = \\ &= \sqrt{100 + 144} = \sqrt{244} \doteq 15{,}620 \text{ km} \end{align*}
Vzdálenost obou cyklistů bude asi 15 km 620 m.
Závěr
V tomto článku jsme si probrali Pythagorovu větu na příkladech, které se týkají o něco složitějších geometrických útvarů nebo jiných matematických problémů, kde se pravoúhlé trojúhelníky nějakým způsobem vyskytují.
V následujícím článku se podíváme na Thaletovu větu.