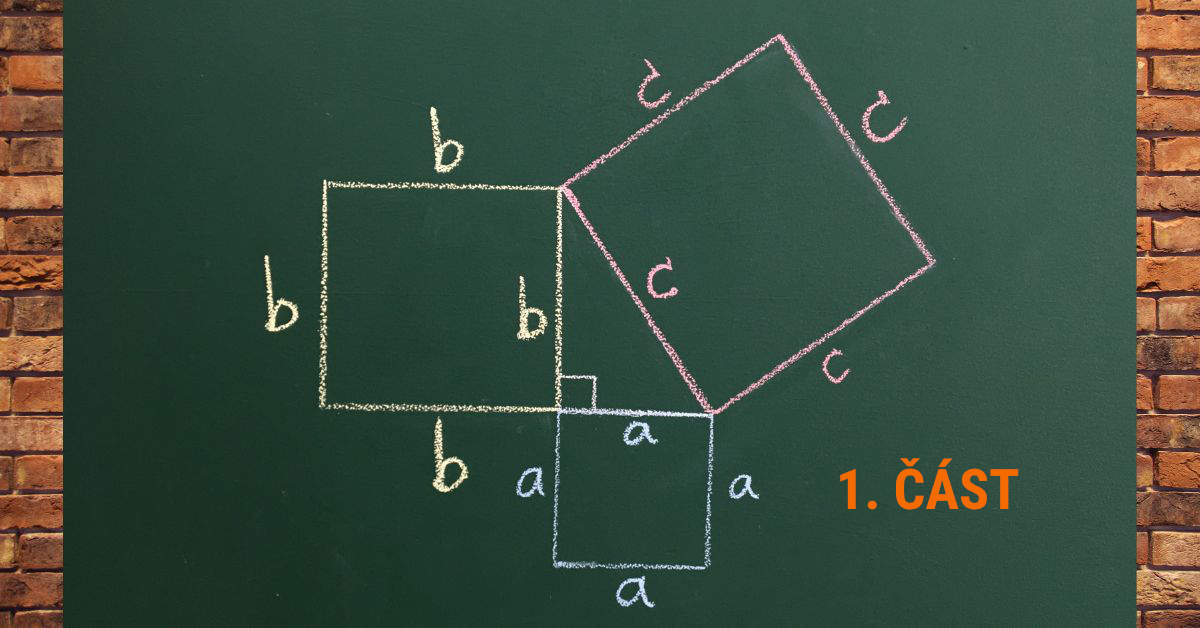Pythagorova věta – 1. část

Vítejte u prvního článku série věnované pravoúhlému trojúhelníku, ve kterém se budeme věnovat Pythagorově větě.

Pythagorova věta je natolik základní věc, se kterou se budete v nejrůznějších geometrických úlohách setkávat prakticky neustále, že jsem toto téma rozdělil do dvou článků. V tomto si Pythagorovu větu definujeme a ukážeme na pravoúhlém trojúhelníku, zatímco v tom příštím si uvedeme ještě několik o něco složitějších geometrických příkladů.

Ze všeho nejdříve je ale potřeba mít jasno ve dvou základních pojmech, které se v souvislosti s pravoúhlým trojúhelníkem používají:

• Přepona je strana, která leží naproti pravému úhlu. Ze všech stran pravoúhlého trojúhelníku je nejdelší. Oba úhly přilehlé k přeponě jsou ostré (tzn. menší než 90°) a jejich součet je 90°. Pravoúhlý trojúhelník má jednu přeponu.
• Odvěsny jsou strany, které spolu svírají pravý úhel. Můžeme také říct, že leží na ramenech pravého úhlu. Pravoúhlý trojúhelník má dvě odvěsny.

Ukažme si obrázek pravoúhlého trojúhelníku:

V tomto obrázku strana AB = c je přepona, strany AC = b, BC = a jsou odvěsny; úhel γ je pravý, úhly α, β jsou ostré a platí pro ně α + β = 90°.

Způsob, kterým si nakreslíte pravoúhlý trojúhelník, když si děláte jeho náčrtek, záleží na vás. Můžete si ho nakreslit jako na obrázku výše nebo také takto:

Pythagorova věta je definována takto:

V pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami roven obsahu čtverce nad přeponou.

Podívejme se na následující obrázek:

Každá z odvěsen je kratší než přepona, takže čtverce sestrojené nad odvěsnami jsou menší, zatímco přepona je nejdelší strana pravoúhlého trojúhelníku, takže čtverec sestrojený nad ní je největší. A Pythagorova věta neznamená nic jiného, než že když sečteme obsahy oněch dvou menších čtverců, dostaneme obsah tohoto největšího čtverce. To je v podstatě celé tajemství. 🙂

Protože obsah čtverce se spočítá jako délka strany umocněná na druhou, tak obsah čtverce nad stranou a je $ a^2 $, obsah čtverce nad stranou b je $ b^2 $ a obsah čtverce nad stranou c je $ c^2 $. Strany a, b jsou v našem obrázku odvěsny a strana c je přepona.

Proto můžeme definovat Pythagorovu větu i takto:

Tato definice je ale jen důsledkem definice vyjádřené výše. Výraz $ c^2 $ vyjadřuje obsah čtverce nad přeponou a výrazy $ a^2 $ a $ b^2 $ vyjadřují obsahy čtverců nad odvěsnami. Tím pádem tento vzorec opět vyjadřuje skutečnost, že obsah čtverce nad přeponou je součtem obsahů čtverců nad odvěsnami.

Toto je dobré si uvědomovat, protože v různých úlohách můžeme mít trojúhelníky označené jinými písmeny nebo i stejnými, ale tak, že strana c nebude přepona ale jedna z odvěsen. Proto než automaticky napíšete $ c^2 = a^2 + b^2 $, tak se vždy podívejte, jestli jsou tak strany v úloze, kterou řešíte, doopravdy označené, a pokud ano, tak jestli je strana c opravdu přepona.

Pythagorova věta umožňuje vypočítat z daných dvou stran pravoúhlého trojúhelníku stranu třetí. Ukážeme si pár příkladů.

Příklad 1

Vypočítejte délku přepony c pravoúhlého trojúhelníku s odvěsnami délek a = 5 cm a b = 8 cm.

Řešení

Podle Pythagorovy věty platí:

$$ c^2 = a^2 + b^2 $$

Dosadíme si do vzorce délky stran a a b a postupně dostaneme:

\begin{align*}
c^2 &= 5^2 + 8^2 \\
c^2 &= 25 + 64 \\
c^2 &= 89
\end{align*}

Dospěli jsme k výsledku, že druhá mocnina délky strany c je rovna číslu 89. Abychom získali samotnou délku strany c, musíme toto číslo odmocnit:

$$ c = \sqrt{89} \doteq 9{,}43 \text{ cm} $$

Protože na konci výpočtu musíme vždy provést druhou odmocninu, můžeme si dát obě strany rovnice pod druhou odmocninu hned od začátku. Druhá odmocnina s $ c^2 $ na levé straně rovnice je ale samotné c. Proto platí:

$$ c = \sqrt{a^2 + b^2} $$

Dosazením délek odvěsen a, b do tohoto vzorce dostaneme délku přepony c rovnou:

\begin{align*}
c &= \sqrt{a^2 + b^2} = \\
&= \sqrt{5^2 + 8^2} = \sqrt{25 + 64} \\
&= \sqrt{89} \doteq 9{,}43 \text{ cm}
\end{align*}

Příklad 2

Vypočítejte délku odvěsny a pravoúhlého trojúhelníku, kde délka druhé odvěsny b = 6 cm a délka přepony c = 9 cm.

Řešení

První způsob řešení je takový, že můžeme dosadit do Pythagorovy věty to, co známe a dopočítat si to, co neznáme:

\begin{align*}
c^2 &= a^2 + b^2 \\
9^2 &= a^2 + 6^2 \\
81 &= a^2 + 36 \qquad |- \; 36 \\
81 \; – \; 36 &= a^2 \\
45 &= a^2 \qquad | \sqrt{} \\
a &\doteq 6{,}71 \text{ cm}
\end{align*}

Jenže my už víme, že Pythagorova věta znamená, že obsah čtverce nad přeponou je součtem obsahů čtverců nad odvěsnami. Proto když délku přepony známe a počítáme délku odvěsny, tak od čtverce nad předponou odečteme čtverec nad tou odvěsnou, kterou známe.

Zapamatujte si tyto tři vzorce:

Nebo si spíš zapamatujte princip, který za nimi vězí:

• Počítáme-li délku přepony, tak čtverce nad odvěsnami sčítáme.
• Počítáme-li délku odvěsny, tak od čtverce nad přeponou odečítáme čtverec druhé (té známé) odvěsny.

Když si jednotlivé strany všech tří výše uvedených vztahů odmocníme, tak získáme vzorce, které nám umožní spočítat délku přepony nebo některé odvěsny rovnou:

Takže náš aktuální příklad můžeme spočítat jednodušeji takto (připomeňme, že počítáme délku odvěsny a, kde délka druhé odvěsny b = 6 cm a délka přepony c = 9 cm):

\begin{align*}
a &= \sqrt{c^2 \; – \; b^2} = \sqrt{9^2 \; – \; 6^2} = \\
&= \sqrt{81 \; – \; 36} = \sqrt{45} \doteq 6{,}71 \text{ cm}
\end{align*}

Obrácená věta k větě Pythagorově

V článku jsme si několikrát ukázali, že pokud je trojúhelník pravoúhlý, platí pro něj Pythagorova věta. Vzniká otázka, zda platí i obráceně, že pokud pro nějaký trojúhelník platí Pythagorova věta, pak je tento trojúhelník pravoúhlý.

Odpověď je ano, platí to i opačně. To nám umožňuje rozhodnout, zda je nebo není nějaký trojúhelník pravoúhlý, pokud známe délky jeho všech tří stran.

Dejme tomu, že máme trojúhelník se stranami k = 8 cm, l = 10 cm a m = 6 cm, a máme určit, zda je tento trojúhelník pravoúhlý.

Pokud pravoúhlý je, pak jeho nejdelší strana je přepona a kratší strany jsou odvěsny. Nejdelší strana našeho trojúhelníku je l a kratší strany jsou k, m. Otestujeme tedy, jestli obsah čtverce nad nejdelší stranou je součtem obsahů čtverců nad kratšími stranami, tedy zda platí:

$$ l^2 = k^2 + m^2 $$

Dosadíme do vztahu odpovídající délky a otestujeme rovnost levé a pravé strany rovnice:

\begin{align*}
10^2 &= 8^2 + 6^2\\
100 &= 64 + 36 \\
100 &= 100
\end{align*}

Získali jsme platnou rovnost, což znamená, že náš trojúhelník je pravoúhlý.

Závěr

V tomto článku jsme si probrali Pythagorovu větu, což je snad nejpoužívanější věta, která se používá v nejrůznějších geometrických úlohách, ale na její principy narazíte i v jiných oblastech matematiky.

Pythagorova věta je bezpochyby jedním ze vstupních bodů do celé matematiky a její znalost patří mezi naprosto fundamentální dovednosti. Z tohoto důvodu si v následujícím článku ukážeme ještě několik dalších příkladů, kde budeme též potřebovat Pythagorovu větu.