Nerovnice v podílovém tvaru - Matematika nejen pro střední školy

V předchozím článku jsme se zabývali nerovnicemi v součinovém tvaru. Ukázali jsme si dvě základní metody jejich řešení – pomocí soustav nerovnic a metodou nulových bodů.

V tomto článku se budeme věnovat nerovnicím v podílovém tvaru. Půjde o nerovnice tvaru „zlomek, v jehož čitateli i jmenovateli je lineární dvojčlen nebo součin několika lineárních dvojčlenů, je větší (menší, větší nebo rovno, menší nebo rovno) než nula“, nebo o nerovnice, které lze na tento tvar převést. V čitateli může také být pouze konstanta (pevně dané číslo).

Budeme postupovat podobně jako v článku o nerovnicích v součinovém tvaru. Pokud neznáte pojmy, které zde budeme používat, doporučuji si nejdřív zmíněný článek přečíst.

Začneme jednoduchým příkladem, který budeme řešit pomocí soustav nerovnic.

Příklad 1

Řešte nerovnici:

$$ \frac{x \; – \; 8}{x + 3} < 0 $$

Rozbor

Tuto nerovnici nemůžeme vynásobit jmenovatelem daného zlomku, aniž bychom určili, kdy je tento jmenovatel kladný nebo záporný, protože při násobení nerovnice záporným číslem musíme otočit znak nerovnosti. Jmenovatel je však záporný jen pro určité hodnoty neznámé x, zatímco pro jiné je kladný!

Kdybychom se chtěli zlomku zbavit, museli bychom řešení rozvětvit a spočítat ho zvlášť na příslušných intervalech – to si ukážeme u příkladu 2 jako 3. způsob jeho řešení. Teď na to půjdeme jinak.

Protože „lomeno“ znamená „děleno“, budeme vycházet z toho, že když dělíme dvě čísla, tak o tom, zda bude výsledek kladný nebo záporný, rozhodují jejich znaménka. Na začátku článku o nerovnicích v součinovém tvaru jsme si uvedli jednoduchou tabulku udávající výsledné znaménko pro násobení dvou čísel. Obdobná tabulka pro dělení dvou čísel vypadá stejně – pouze v ní místo operátorů „krát“ máme operátory „děleno“ – viz následující obrázek:

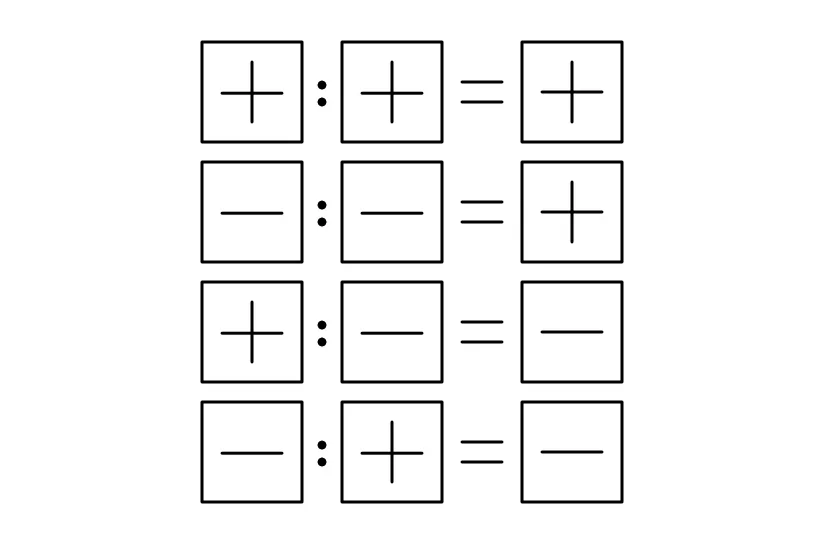
Z této tabulky je patrné, že dvě stejná znaménka nám při dělení dají kladný výsledek, zatímco dvě různá znaménka nám při dělení dají záporný výsledek.

Zlomek na levé straně naší nerovnice má být menší než nula, tzn. že má být záporný. To nastane tehdy, když čitatel zlomku bude kladný – tedy větší než nula, a jmenovatel bude záporný – tedy menší než nula, nebo to bude celé opačně: čitatel zlomku bude záporný a jmenovatel kladný.

Číslo x je proto řešením naší nerovnice právě tehdy když:

$ x \; – \; 8 > 0 $ a zároveň $ x + 3 < 0 $

nebo

$ x \; – \; 8 < 0 $ a zároveň $ x + 3 > 0 $

Což znamená, že číslo x je řešením naší nerovnice právě tehdy, když je řešením některé ze soustav lineárních nerovnic:

\begin{align*}
x \; – \; 8 &> 0 \\
x + 3 &<0
\end{align*}

nebo:

\begin{align*}
x \; – \; 8 &<0 \\
x + 3 &>0
\end{align*}

Řešení

Z první soustavy dostaneme $ x > 8 $ a zároveň $ x < -3 $. Tato soustava nemá žádné řešení, protože nemůže existovat takové číslo, které je větší než 8 a zároveň menší než -3. Množina K₁ řešení této soustavy je tedy prázdná množina:

$$ K_1 = \emptyset $$

Z druhé soustavy dostaneme $ x < 8 $ a zároveň $ x > -3 $. Množina K₂ řešení této soustavy je interval:

$$ K_2 = (-3; 8) $$

Množinou K všech řešení naší nerovnice je sjednocení množin všech řešení obou soustav:

\[ K = K_1 \cup K_2 = \emptyset \cup (-3; 8) = (-3; 8) \]

(Když provedeme sjednocení jedné množiny s prázdnou množinou, tak se nic nestane – je to podobné, jako když při sčítání přičteme k výsledku nulu – také se na tomto výsledku nic nezmění.)

Příklad 2

Řešte nerovnici:

$$ \frac{x \; – \; 2}{x + 6} \geqq -2 $$

Rozbor

Ani tuto nerovnici nemůžeme vynásobit jmenovatelem zlomku bez upřesnění, zda je tento jmenovatel kladný nebo záporný, ze stejného důvodu jako u prvního příkladu.

Zároveň nemůžeme použít logiku „podíl dvou čísel se stejnými znaménky nám dá kladný výsledek, podíl dvou čísel s opačnými znaménky nám dá záporný výsledek“, protože na pravé straně nerovnice nemáme číslo nula, které „odděluje“ kladná čísla od záporných, ale -2.

Abychom tuto logiku použít mohli, musíme nejdřív nerovnici upravit tak, aby na její pravé straně bylo číslo nula. To uděláme tak, že k oběma stranám nerovnice přičteme číslo 2 a potom její levou stranu upravíme, abychom na ní měli jediný zlomek. (Tuto úpravu provedeme sečtením zlomku a tohoto čísla přes společný jmenovatel).

\begin{align*} \frac{x \; – \; 2}{x + 6} &\geqq -2 \qquad |+2 \\ \frac{x \; – \; 2}{x + 6} + 2 &\geqq 0 \\ \frac{x \; – \; 2 + 2(x + 6)}{x + 6} &\geqq 0 \\ \frac{x \; – \; 2 + 2x + 12}{x + 6} &\geqq 0 \\ \frac{3x + 10}{x + 6} &\geqq 0 \end{align*}

Získali jsme novou nerovnici, jejíž řešení je ekvivalentní jako u původní nerovnice, přičemž na pravé straně máme číslo 0, takže můžeme postupovat buď skrze soustavy nerovnic nebo metodou nulových bodů.

1. způsob řešení – soustavy nerovnic

Zlomek na levé straně nerovnice

$$ \frac{3x + 10}{x + 6} \geqq 0 $$

má být větší nebo rovno nula, tzn. nezáporný (kladný nebo nulový). To nastane buď tehdy, když:

čitatel zlomku bude nezáporný (větší nebo roven nule) a jmenovatel kladný (větší než nula), nebo
čitatel zlomku bude nekladný (nulový nebo záporný, tj. menší nebo roven nule) a jmenovatel záporný (menší než nula).

Ještě dodejme, že jmenovatel zlomku nesmí být nulový, protože by došlo k dělení nulou.

Sestavíme si tedy dvě soustavy lineárních nerovnic. První pro zmíněný nezáporný čitatel a kladný jmenovatel:

\begin{align*}
3x + 10 &\geqq 0 \\
x + 6 &> 0
\end{align*}

a druhou pro zmíněný nekladný čitatel a záporný jmenovatel:

\begin{align*}
3x + 10 &\leqq 0\\
x + 6 &< 0
\end{align*}

Z první soustavy dostaneme $ x \geqq -\frac{10}{3} $ a zároveň $ x > -6 $. Množinou K₁ všech řešení této soustavy je interval:

$$ K_1 = \bigg\langle {-}\frac{10}{3}; +\infty\bigg) $$

Viz následující obrázek:

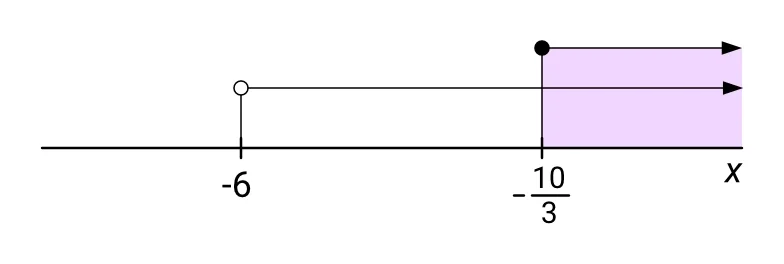
(Při kreslení obrázků s intervaly je důležité zobrazit si na osu čísla podle velikosti. Číslo -6 je menší než číslo $ -\frac{10}{3} $, proto je na obrázku více vlevo. Číslo $ -\frac{10}{3} $ je zhruba -3,33, což je větší hodnota než -6, proto je na obrázku více vpravo.)

Z druhé soustavy dostaneme $ x \leqq -\frac{10}{3} $ a zároveň $ x < -6 $. Množinou K₂ všech řešení této soustavy je interval:

$$ K_2 = (-\infty; -6) $$

Viz následující obrázek:

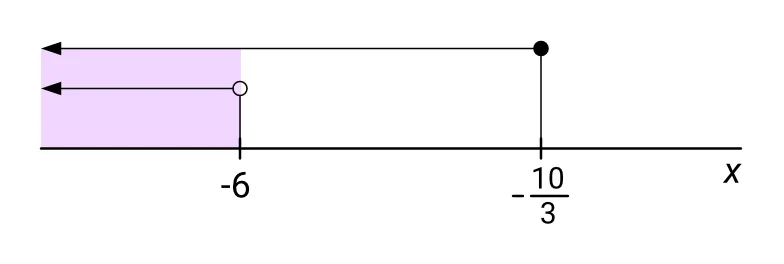
Množinou K všech řešení celé nerovnice je sjednocení množin (intervalů) řešení obou soustav:

\[ K = K_1 \cup K_2 = (-\infty; -6) \cup \bigg\langle {-}\frac{10}{3}; +\infty\bigg) \]

Viz následující obrázek:

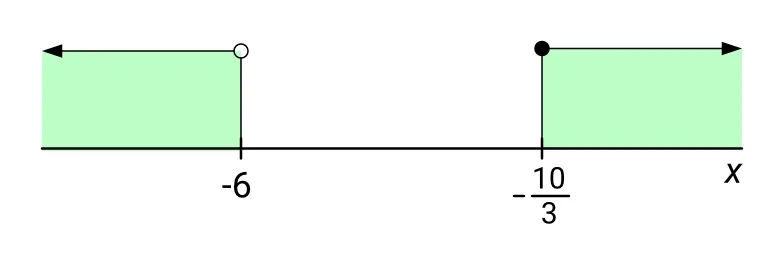
Připomeňme, že tam, kde používáme spojku „a zároveň“, děláme průnik, a tam, kde používáme spojku „nebo“, děláme sjednocení.

2. způsob řešení – metoda nulových bodů

Vyjdeme z upravené nerovnice, kde máme na pravé straně nulu:

$$ \frac{3x + 10}{x + 6} \geqq 0 $$

Krok 1 – stanovíme nulové body

Stanovíme nulové body lineárních dvojčlenů v čitateli a jmenovateli zlomku na levé straně nerovnice. Nulový bod je takové číslo, které po dosazení za neznámou do daného lineárního dvojčlenu způsobí, že tento dvojčlen bude mít hodnotu 0.

Nulový bod lineárního dvojčlenu $ 3x + 10 $ je číslo $ -\frac{10}{3} $ a nulový bod lineárního dvojčlenu $ x + 6 $ je číslo -6.

Nulové body nám rozdělí množinu reálných čísel na tři intervaly – viz následující obrázek:

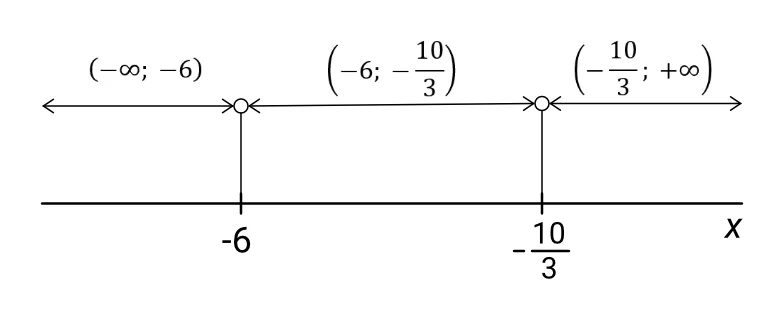
Krok 2 – sestavíme tabulku

Nakreslíme si tabulku, jejíž sloupce budou odpovídat intervalům a nulovým bodům, přičemž všechny hodnoty seřadíme podle velikosti od nejmenších po největší. Druhý a třetí řádek tabulky bude odpovídat prvnímu a druhému lineárnímu dvojčlenu (tedy čitateli a jmenovateli zlomku na levé straně nerovnice). Poslední řádek pak bude odpovídat jejich podílu, tj. celému zlomku.

Do jednotlivých políček zapíšeme, jaké znaménko bude mít daný dvojčlen v příslušném intervalu. Výsledné znaménko celého zlomku pak určíme pomocí pravidel pro dělení znamének (podíl dvou stejných znamének dá plus, podíl dvou různých znamének dá minus a podíl nuly a jakéhokoli nenulového výrazu dá nulu).

$ x $	$ (-\infty; -6) $	$ -6 $	$ \big({-}6; -\frac{10}{3}\big) $	$ -\frac{10}{3} $	$ \big({-}\frac{10}{3}; +\infty\big) $
$ 3x + 10 $	$ – $	$ – $	$ – $	$ 0 $	$ + $
$ x + 6 $	$ – $	0	$ + $	$ + $	$ + $
$ \frac{3x + 10}{x + 6} $	$ + $	nedef.	$ – $	$ 0 $	$ + $

(Protože nulou dělit nelze, je v posledním řádku ve sloupci odpovídajícímu číslu -6 napsáno „nedef.“ jako „nedefinováno“.)

3. krok – z posledního řádku tabulky určíme řešení

Protože zlomek na levé straně nerovnice má být nezáporný (větší nebo rovno nule), řešením nerovnice je sjednocení těch množin, u nichž v posledním řádku tabulky máme buď znaménko plus nebo nulu. Znaménko plus máme u intervalů $ (-\infty; -6) $ a $ \big({-}\frac{10}{3}; +\infty\big) $. Nulu máme u čísla $ -\frac{10}{3} $, které z levé strany přiléhá k intervalu $ \big({-}\frac{10}{3}; +\infty\big) $, takže ho můžeme do tohoto intervalu zahrnout, čímž se interval stane z levé strany uzavřený.

Množina K kořenů naší nerovnice bude tedy vypadat takto:

\[ K = (-\infty; -6) \cup \bigg\langle {-}\frac{10}{3}; +\infty\bigg) \]

3. způsob řešení – odstranění zlomku

Na začátku článku jsme psali o tom, že nerovnici v podílovém tvaru nemůžeme vynásobit jmenovatelem daného zlomku, aniž bychom určili, pro jaké hodnoty neznámé tak činíme. Pokud to tedy chceme udělat, musíme nejdřív stanovit, kdy bude tento zlomek záporný a kdy kladný, abychom se mohli rozhodnout, zda máme nebo nemáme otočit znak nerovnosti.

Vraťme se k naší původní nerovnici:

$$ \frac{x \; – \; 2}{x + 6} \geqq -2 $$

Aby měl zlomek v této nerovnici smysl, musí být $ x \neq -6 $. Nerovnici tedy řešíme v množině $ R \; – \; \{-6\} $. Chceme-li zlomek odstranit, musíme nerovnici vynásobit výrazem $ x + 6 $. Abychom to mohli udělat, musíme vědět, jaké má tento výraz znaménko. Proto množinu $ R \; – \; \{-6\} $ rozdělíme na dva intervaly dle nulového bodu tohoto výrazu, v nichž výraz $ x + 6 $ nemění znaménko, a v každém z nich vyřešíme nerovnici zvlášť.

Prvním takovým intervalem je $ (-\infty; -6) $ a druhým $ (-6; +\infty) $

a) Vyřešíme nerovnici v intervalu $ (-\infty; -6) $: výraz $ x + 6 $ je pro všechny hodnoty z tohoto intervalu záporný, takže při vynásobení nerovnice tímto výrazem musíme otočit znak nerovnosti:

\begin{align*} \frac{x \; – \; 2}{x + 6} &\geqq -2 \qquad | \cdot (x + 6) < 0 \\ x \; – \; 2 &\leqq -2(x + 6) \\ x \; – \; 2 &\leqq -2x \; – \; 12 \qquad |+2x + 2 \\ 3x &\leqq -10 \qquad |:3 \\ x &\leqq -\frac{10}{3} \end{align*}

Z čísel patřících do intervalu $ (-\infty; -6) $ jsou tedy řešením nerovnice ta, pro která platí $ x \leqq -\frac{10}{3} $, tzn. která patří do intervalu $ \big({-}\infty; -\frac{10}{3}\big\rangle $. Množina K₁ těchto řešení je tedy průnikem tohoto intervalu a intervalu, ve kterém nerovnici řešíme:

\[ K_1 = \bigg({-}\infty; -\frac{10}{3}\bigg\rangle \cap (-\infty; -6) = (-\infty; -6) \]

b) Vyřešíme nerovnici v intervalu $ (6; +\infty) $: výraz $ x + 6 $ je pro všechny hodnoty z tohoto intervalu kladný, takže při vynásobení nerovnice tímto výrazem nebudeme otáčet znak nerovnosti:

\begin{align*} \frac{x \; – \; 2}{x + 6} &\geqq -2 \qquad | \cdot (x + 6) > 0 \\ x \; – \; 2 &\geqq -2(x + 6) \\ x \; – \; 2 &\geqq -2x \; – \; 12 \qquad |+2x + 2 \\ 3x &\geqq -10 \qquad |:3 \\ x &\geqq -\frac{10}{3} \end{align*}

Z čísel patřících do intervalu $ (-6; +\infty) $ jsou tedy řešením nerovnice ta, pro která platí $ x \geqq -\frac{10}{3} $, tzn. která patří do intervalu $ \big({-}\frac{10}{3}; +\infty\big) $. Množina K₂ těchto řešení je tedy průnikem tohoto intervalu a intervalu, ve kterém nerovnici řešíme:

\[ K_2 = \bigg\langle{-}\frac{10}{3}; +\infty\bigg) \cap (-6; +\infty) = \bigg\langle {-}\frac{10}{3}; +\infty\bigg) \]

Množinu K celkového řešení nerovnice získáme jako sjednocení množin jejích řešení v obou uvažovaných intervalech:

\[ K = K_1 \cup K_2 = (-\infty; -6) \cup \bigg\langle {-}\frac{10}{3}; +\infty\bigg) \]

Příklad 3

Metoda nulových bodů je zvláště vhodná pro složitější příklady, proto si na závěr jeden takový příklad ukážeme.

Řešte nerovnici:

\[ \frac{x + 1}{x + 2} \; – \; \frac{4 \; – \; x}{1 \; – \; x} \leqq 0 \]

Řešení

Zlomky na levé straně nerovnice od sebe odečteme tak, abychom získali zlomek jediný:

\begin{align*} \frac{x + 1}{x + 2} \; – \; \frac{4 \; – \; x}{1 \; – \; x} \leqq 0 \\ \frac{(1 \; – \; x)(x + 1) \; – \; (x + 2)(4 \; – \; x)}{(x + 2)(1 \; – \; x)} \leqq 0 \\ \frac{x + 1 \; – \; x^2 \; – \; x \; – \; 4x + x^2 \; – \; 8 + 2x}{(x + 2)(1 \; – \; x)} \leqq 0 \\ \frac{-2x \; – \; 7}{(x + 2)(1 \; – \; x)} \leqq 0 \\ \end{align*}

Určíme nulové body lineárních dvojčlenů na levé straně nerovnice:

dvojčlen $ -2x \; – \; 7 $ z čitatele zlomku má nulový bod $ -\frac{7}{2} $,
dvojčlen $ x + 2 $ z první závorky ve jmenovateli zlomku má nulový bod $ -2 $,
dvojčlen $ 1 \; – \; x $ z druhé závorky ve jmenovateli zlomku má nulový bod $ 1 $.

Tyto tři nulové body nám rozdělí množinu reálných čísel na čtyři intervaly – viz následující obrázek:

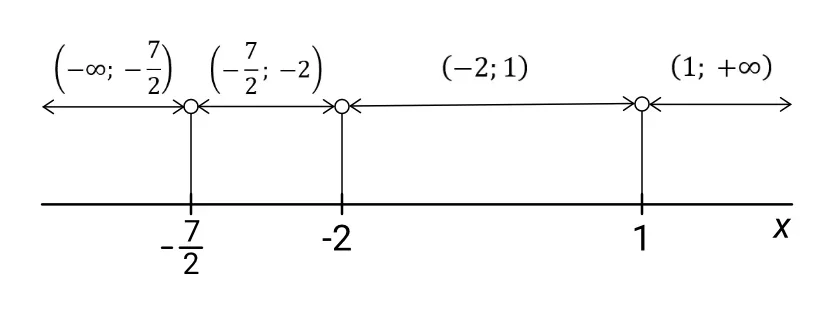
Sestavíme tabulku stejným způsobem jako v předchozím příkladu, pouze místo dvou lineárních dvojčlenů budeme mít tři. Znaménko v posledním řádku se v případě více než dvou lineárních dvojčlenů určuje podle následujícího pravidla: Jsou-li všichni činitelé v čitateli i jmenovateli nenuloví, potom výsledné znaménko bude minus právě tehdy, když lichý počet těchto činitelů je záporných.

To znamená, že když je v některém sloupci odpovídajícím některému z intervalů nebo nulových bodů číslo 0, tak v posledním řádku v daném políčku bude buď nula nebo „nedefinováno“ (podle toho, zda číslo 0 dosazujeme do dvojčlenu v čitateli nebo jmenovateli zlomku). Pokud máme v daném sloupci pouze znaménka plus nebo minus, pak lichý počet znamének minus dá výsledek minus a sudý počet znamének minus dá výsledek plus.

Naše tabulka bude tedy vypadat takto:

$ x $	$ \big({-}\infty; -\frac{7}{2}\big) $	$ -\frac{7}{2} $	$ \big({-}\frac{7}{2}; -2\big) $	$ -2 $	$ (-2; -1) $	$ -1 $	$ (-1; +\infty) $
$ -2x \; – \; 7 $	$ + $	$ 0 $	$ – $	$ – $	$ – $	$ – $	$ – $
$ x + 2 $	$ – $	$ – $	$ – $	$ 0 $	$ + $	$ + $	$ + $
$ 1 \; – \; x $	$ + $	$ + $	$ + $	$ + $	$ + $	$ 0 $	$ – $
$ L(x) $	$ – $	$ 0 $	$ + $	nedef.	$ – $	nedef.	$ + $

Výrazem $ L(x) $ se myslí celá levá strana nerovnice, abychom nemuseli opisovat celý složitý zlomek. 🙂

Zlomek na levé straně naší nerovnice:

\[ \frac{-2x \; – \; 7}{(x + 2)(1 \; – \; x)} \leqq 0 \]

má být menší nebo rovno 0, tj. nekladný (záporný nebo nula). To znamená, že řešením nerovnice jsou taková čísla x, pro která máme v posledním řádku tabulky znaménko minus nebo číslo 0. Znaménko minus máme u intervalů $ \big({-}\infty; -\frac{7}{2}\big) $ a $ (-2; -1) $ a nulu u čísla $ -\frac{7}{2} $. Toto číslo z pravé strany přiléhá k intervalu $ \big({-}\infty; -\frac{7}{2}\big) $, takže když ho s ním sloučíme, stane se tento interval na pravé straně uzavřeným.

Množina K všech řešení naší nerovnice bude tedy následující:

\[ K = \bigg({-}\infty; -\frac{7}{2}\bigg\rangle \cup (-2; -1) \]

Závěr

V tomto článku jsme podrobně probrali nerovnice v podílovém tvaru, což jsou v podstatě nerovnice s neznámou ve jmenovateli. Vysvětlili jsme si, že zlomku se jmenovatelem, který obsahuje neznámou, se v nerovnici nemůžeme zbavit prostým vynásobením nerovnice tímto jmenovatelem, a ukázali jsme si tři různé metody řešení, z nichž nejpoužívanější je metoda nulových bodů.

Tímto článkem jsme zakončili naši sérii o lineárních nerovnicích. Pokud jste si příslušné články prostudovali, máte vybudovaný slušný základ v této oblasti, který se vám bude hodit i u některých dalších speciálních rovnic a nerovnic.