Násobení vektoru číslem

V předchozím článku jsme se zabývali sčítáním a odčítáním vektorů.

V tomto článku budeme ve vektorové aritmetice pokračovat – ukážeme si další operaci, kterou můžeme s vektory provádět, a sice násobení vektoru číslem. Nejde tedy ještě o vzájemné násobení dvou vektorů, protože jeden operand je číslo a druhý vektor – násobíme tedy jeden vektor nějakým číslem.

Definice násobení vektoru číslem

Vektor vynásobíme číslem tak, že tímto číslem vynásobíme jeho souřadnice. Vektor u vynásobený číslem k označujeme symbolem ku. Odtud můžeme uvést definici násobení vektoru číslem:

Vynásobený vektor si samozřejmě můžeme pojmenovat libovolným písmenem, např. jako v = ku.

Zachování směru nebo otočení do opačného směru

Pokud vynásobíme vektor číslem, pak výsledný vektor bude mít buď stejný směr jako původní vektor, nebo bude mít směr opačný. Násobení vektoru číslem je tedy stejné, jako bychom daný vektor pouze prodlužovali nebo zkracovali, nebo ho „protahovali na opačnou stranu“, ale neotáčeli s ním.

Pojďme se podívat na různé varianty, jak bude vypadat vynásobený vektor ve srovnání s původním pro různá čísla, kterými ho budeme násobit.

Následující obrázek znázorňuje situaci, kdy je vektor v dvojnásobkem vektoru u, tedy platí $ \boldsymbol{v} = 2 \boldsymbol{u} $:

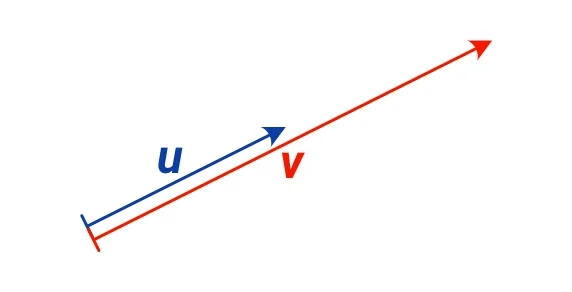
Vidíme, že vektor v má stejný směr jako vektor u, ale má dvakrát větší velikost. Násobení vektoru číslem větším než 1 tedy způsobí prodloužení vektoru.

Na dalším obrázku má vektor v poloviční velikost oproti vektoru u a rovněž stejný směr, tedy platí $ \boldsymbol{v} = \frac{1}{2} \boldsymbol{u} $:

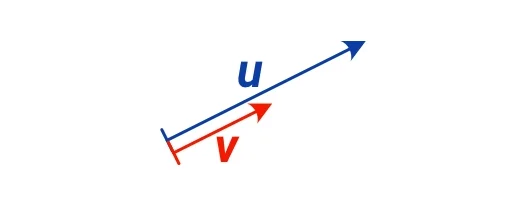
Násobení vektoru číslem menším než 1 ale větším než 0 tedy způsobí zkrácení vektoru.

Další obrázek ukazuje vektor v, který je minus dvojnásobkem vektoru u a má přesně opačný směr, tedy platí $ \boldsymbol{v} = -2 \boldsymbol{u} $:

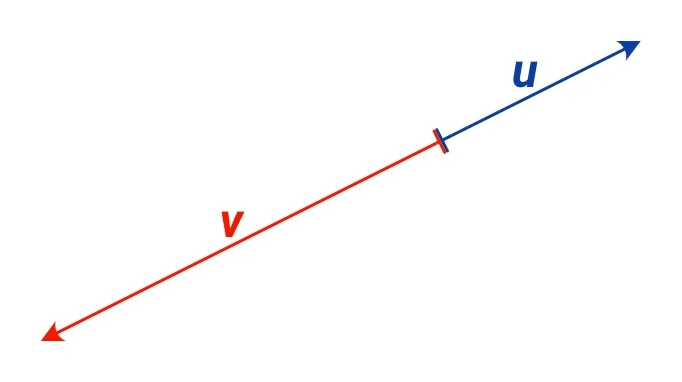
Násobení vektoru záporným číslem způsobí, že výsledný vektor bude směřovat do opačného směru, a bude mít buď větší nebo menší velikost než původní vektor, podle toho, zda ho budeme násobit číslem menším než -1 nebo číslem v intervalu (-1; 0).

Další obrázek ukazuje vektor v, který je minus jedna násobkem vektoru u, tedy platí $ \boldsymbol{v} = -1 \boldsymbol{u} = -\boldsymbol{u} $:

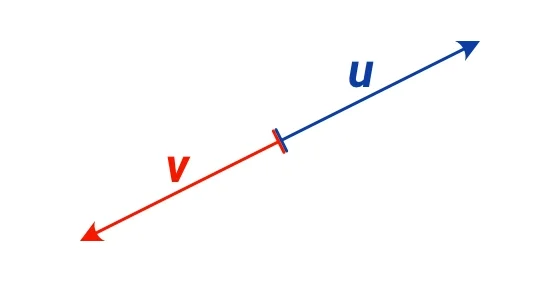
Vynásobení vektoru číslem -1 způsobí, že výsledný vektor bude mít stejnou velikost ale opačný směr, což znamená, že získáme opačný vektor k původnímu vektoru.

Ze všech obrázků je patrné, že kdybychom si původní vektor i jeho násobky kreslili na stejnou přímku, pak všechny vektory zůstanou ležet na této přímce. Tzn. že z ní žádný vektor „neuhne“. Následující obrázek zobrazuje vektor u, který má počátek v bodě A, a dále několik jeho násobků, které mají všechny také počátek v bodě A:

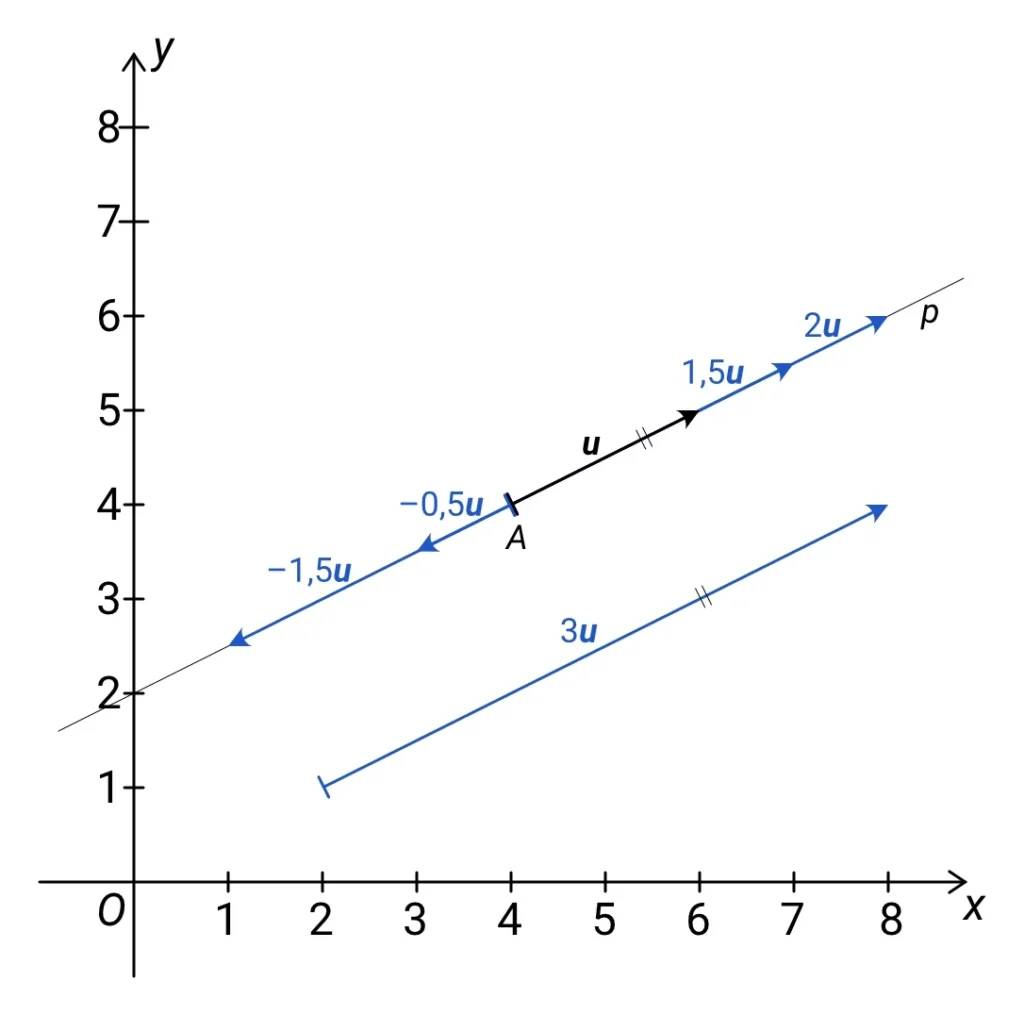
Jak můžeme vidět, všechny tyto vektory leží na stejné přímce p. Když tedy budeme násobit vektor u různými čísly tak, že všechny tyto vynásobené vektory budou začínat v bodě A, kde začíná i vektoru u, pak budeme dostávat různé body jediné přímky procházející bodem A jakožto koncové body těchto vynásobených vektorů. Jak uvidíme v jednom z příštích článků, existuje definice, kde je přímka skutečně určena pomocí bodu a vektoru.

To však neznamená, že násobky vektoru musíme kreslit na stejnou přímku, protože v analytické geometrii si můžeme vyznačit vektor do libovolného místa souřadného systému, ale znamená to, že všechny vektory, které jsou násobkem jiného vektoru, jsou rovnoběžné, jak můžeme vidět na obrázku, kde je vyznačen i vektor 3u.

Kombinace násobení vektorů čísly se sčítáním vektorů

Když zkombinujeme násobení vektorů čísly se sčítáním vektorů, dostaneme výraz, kde má násobení přednost, stejně jako v běžné aritmetice. Výsledkem takového výrazu bude nový vektor. Ukažme si to na následujícím příkladu:

Příklad 1

Jsou dány vektory u = (3; -1; 1), v = (1; 2; 5). Vypočítejte souřadnice vektoru w daného výrazem w = 2u + 3v.

Řešení

\begin{align*} \boldsymbol{w} &= 2\boldsymbol{u} + 3\boldsymbol{v} = 2(3; -1; 1) + 3(1; 2; 5) = \\ &= (6; -2; 2) + (3; 6; 15) = (6 + 3; -2 + 6; 2 + 15) = \\ &= (9; 4; 17) \end{align*}

Lineární kombinace vektorů

S touto kombinací násobení vektorů čísly a sčítáním souvisí pojem lineární kombinace vektorů. Uvedeme si její definici a poté blíže objasníme, o co jde:

Vektor au + bv + cw, kde a, b, c $ \in $ R, se nazývá lineární kombinace vektorů u, v, w. Můžeme vytvořit lineární kombinaci i dvou, čtyř, pěti atd. vektorů. Lineární kombinace jednoho vektoru je jeho násobek.

Jak to lépe pochopit? Představte si, že máme v rovině tři různé vektory, které si nakreslíme například tak, aby měli počátek ve stejném bodě. Pokud můžeme některý z těchto vektorů získat tak, že sečteme násobky zbývajících dvou, pak je tento vektor lineární kombinací těchto dvou vektorů. Na následujícím obrázku je vektor w lineární kombinací vektorů u, v, protože ho můžeme získat jako součet trojnásobku vektoru u a dvojnásobku vektoru v:

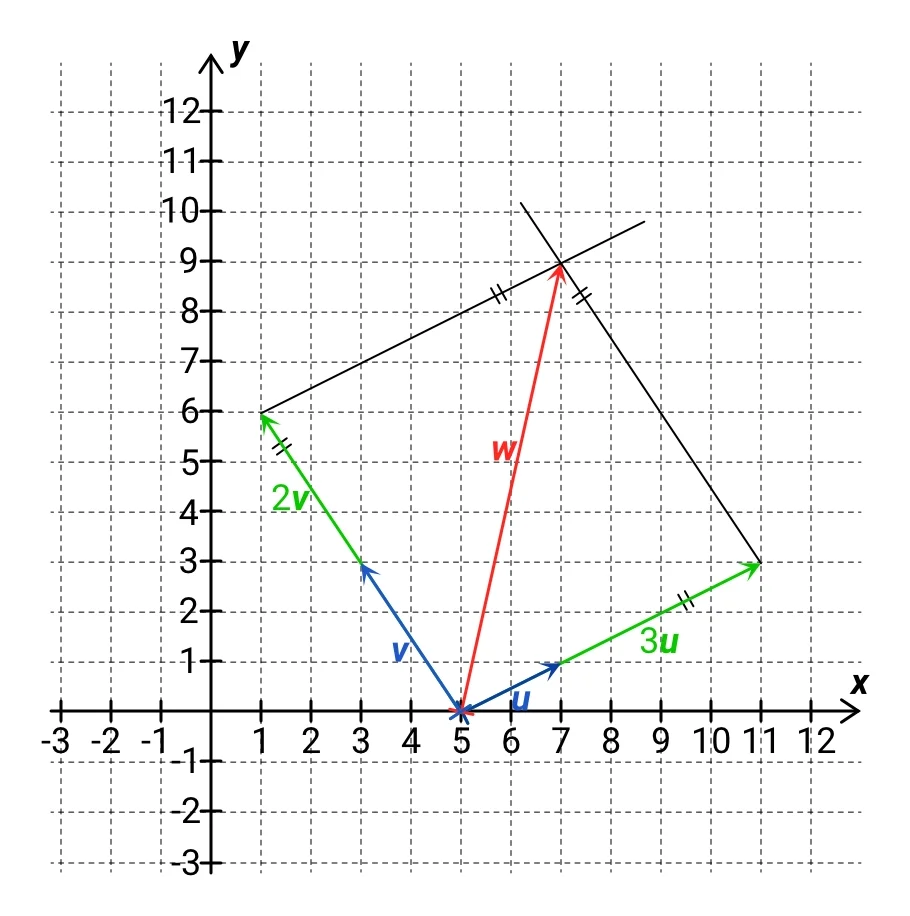
Na dalším obrázku máme jiný vektor w, který jsme získali jako součet minus dvojnásobku vektoru u a minus jednonásobku vektoru v:

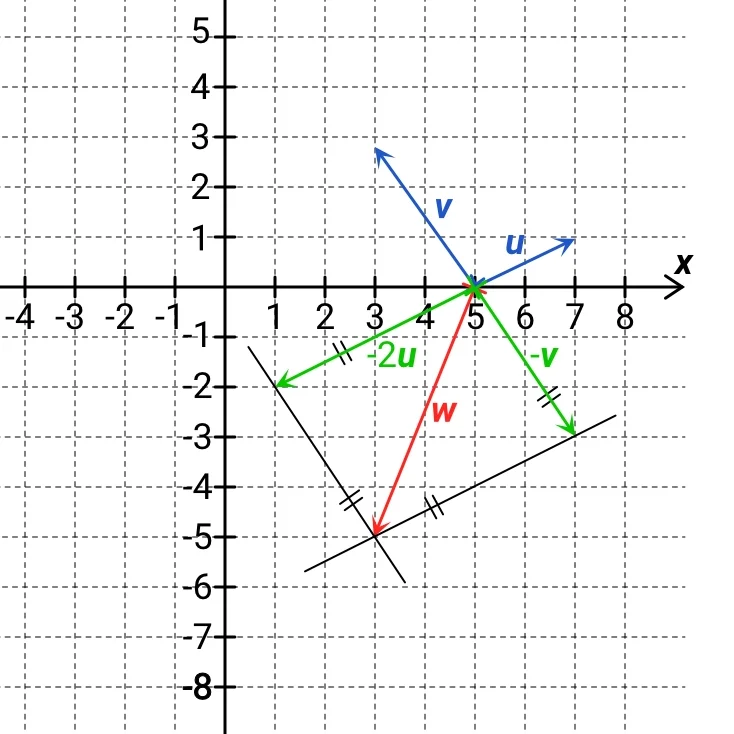
V obou případech tedy platí, že vektor w je lineární kombinací vektorů u, v.

A takto bychom mohli pokračovat. Protože násobení vektoru číslem daný vektor v podstavě prodlouží nebo zkrátí, tak bychom vždycky našli taková čísla, kterými bychom naše vektory u, v mohli vynásobit, abychom po sečtení těchto násobků (např. doplněním na rovnoběžník) dostali vektor w s libovolnými souřadnicemi.

Stejně tak bychom ale našli i čísla, kterými je třeba vynásobit vektory u, w, abychom po sečtení těchto násobků dostali vektor v, což znamená, že vektor v je lineární kombinací vektorů u, w. Obdobně bychom našli čísla, kterými je třeba vynásobit vektory v, w, abychom po sečtení těchto násobků dostali vektor u, což znamená, že vektor u je lineární kombinací vektorů v, w. Takže libovolný vektor z trojice z předchozích dvou obrázků je lineární kombinací zbývajících dvou vektorů. Kdybychom vynásobili všechny tři vektory nějakými čísly a tyto násobky sečetli, dostali bychom vektor, který by byl lineární kombinací těchto tří vektorů.

Toto všechno ale platí jenom v případě, že tyto naše vektory leží v rovině a žádné dva z nich nejsou rovnoběžné (nelze je nakreslit na stejnou přímku). V prostoru bychom potřebovali čtyři nenulové vektory, z nichž žádné tři nelze zakreslit do jedné roviny, abychom mohli říct, že jakýkoli z nich je lineární kombinací ostatních.

Následující obrázek zobrazuje situaci, kdy vektor w není lineární kombinací vektorů u, v:

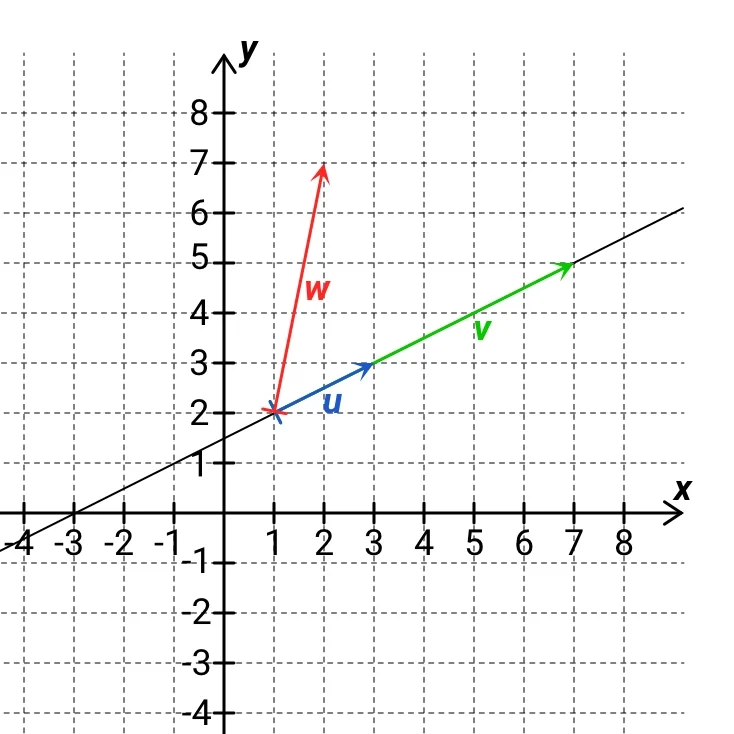
Vektory u, v leží na jedné přímce. Pokud je budeme násobit libovolnými čísly a následně sčítat, jako výsledek vždy obdržíme vektor, který stále leží na této přímce.

Protože u vektorů není důležité, kam si je v souřadném systému nakreslíme, ale záleží na jejich směru a velikosti, mohli bychom si vektory u, v nakreslit i tak, aby neleželi na stejné přímce, ale stále by byly rovnoběžné. To znamená, že jako jejich lineární kombinaci bychom vždy obdrželi vektor, který je s nimi rovněž rovnoběžný. Vektor w však není s vektory u, v rovnoběžný, a proto není jejich lineární kombinací.

Příklad 2

Jsou dány vektory u = (1; 3), v = (–1; 4). Vypočítejte lineární kombinaci 2u – 3v.

Řešení:

\begin{align*} 2 \boldsymbol{u} -3\boldsymbol{v} &= 2(1; 3) -3(-1; 4) = \\ &= (2; 6) + (3; -12) = (5; -6) \end{align*}

Příklad 3

Jsou dány vektory u = (–3; –1; 5), v = (1; 0; –1). Vypočítejte lineární kombinaci 2u – 2v.

Řešení

\begin{align*} 2 \boldsymbol{u} -2\boldsymbol{v} &= 2(-3; -1; 5) -2(1; 0; -1) = \\ &= (-6; -2; 10) + (-2; 0; 2) = (-8; -2; 12) \end{align*}

Příklad 4

Zjistěte, zda vektor u je lineární kombinací vektorů a, b.

a) u = (-2; 4; -6), a = (1; 3; –2), b = (2; 1; 1)
b) u = (1; 1; 2), a = (–1; 0; 1), b = (2; 2; 3)

Řešení

Aby vektor u byl lineární kombinací vektorů a, b, musí existovat čísla, kterými vynásobíme vektory a, b tak, abychom po sečtení těchto násobků dostali vektor u. Označme tato čísla jako p, q. Pak musí platit:

$$ \boldsymbol{u} = p \boldsymbol{a} + q \boldsymbol{b} $$

a) Musí tedy platit:

\begin{align*} (u_1; u_2; u_3) &= p(a_1; a_2; a_3) + q(b_1; b_2; b_3) \\ (-2; 4; -6) &= p(1; 3; -2) + q(2; 1; 1) \\ \hline \\ u_1 &= a_1p + b_1q \\ u_2 &= a_2p + b_2q \\ u_3 &= a_3p + b_3q \\ \hline \\ -2 &= p + 2q \\ 4 &= 3p + q \\ -6 &= -2p + q \\ \hline \end{align*}

Máme soustavu tří rovnic o dvou neznámých. Spočítáme čísla p, q např. z druhé a třetí rovnice:

\begin{align*} 4 &= 3p + q \\ -6 &= -2p + q \qquad | \cdot(-1) \\ \hline \\ 4 &= 3p + q \\ 6 &= 2p -q \qquad | \cdot(-1) \\ \hline \\ 10 &= 5p \qquad |:5 \\ p &= 2 \end{align*}

\begin{align*} 4 &= 3p + q \\ 4 &= 3 \cdot 2 + q \\ 4 &= 6 + q \qquad |-6 \\ q &= -2 \end{align*}

A ověříme, zda vypočítané hodnoty jsou i řešením první rovnice:

\begin{align*} -2 &= p + 2q \\ -2 &= 2 + 2 \cdot(-2) \\ -2 &= 2 -4 \\ -2 &= -2 \end{align*}

Získali jsme platnou rovnost, což znamená, že vypočítané hodnoty p, q jsou řešením všech tří rovnic. Vektor u je proto lineární kombinací vektorů a, b.

b) V tomto případě by muselo platit:

\begin{align*} (u_1; u_2; u_3) &= p(a_1; a_2; a_3) + q(b_1; b_2; b_3) \\ (1; 1; 2) &= p(-1; 0; 1) + q(2; 2; 3) \\ \hline \\ u_1 &= a_1p + b_1q \\ u_2 &= a_2p + b_2q \\ u_3 &= a_3p + b_3q \\ \hline \\ 1 &= -p + 2q \\ 1 &= 2q \\ 2 &= p + 3q \\ \hline \end{align*}

Z druhé rovnice vypočítáme hodnotu q, kterou dosadíme do první rovnice a vypočítáme hodnotu p:

\begin{align*} 1 &= 2q \qquad |:2 \\ q &= \frac{1}{2} \end{align*}

\begin{align*} 1 &= -p + 2q \\ 1 &= -p + 2 \cdot \frac{1}{2} \\ 1 &= -p + 1 \qquad |-1 \\ 0 &= -p \qquad | \cdot (-1) \\ p &= 0 \end{align*}

A ověříme, zda vypočítané hodnoty jsou i řešením třetí rovnice:

\begin{align*} 2 &= p + 3q \\ 2 &= 0 + 3 \cdot \frac{1}{2} \\ 2 &\neq \frac{3}{2} \end{align*}

Dostali jsme neplatnou rovnost. Soustava rovnic, kterou jsme řešili, nemá řešení. Vektor u proto není lineární kombinací vektorů a, b.

Závěr

V tomto článku jsme se zabývali násobením vektoru číslem, což je operace, která se často používá v kombinaci se sčítáním a odčítáním vektorů. Tyto operace úzce souvisí s pojmem lineární kombinace vektorů.

V následujícím článku se podíváme na skalární součin vektorů.