V předchozím článku jsme se věnovali lineární lomené funkci. V tomto a příštím článku se podíváme na mocninné funkce. Pokud jste pochopili kvadratickou funkci a nepřímou úměrnost, které jsme probírali v předchozích článcích, mocninné funkce by pro vás neměly být problém.
Společný úvod k mocninným funkcím
Obecný předpis každé mocninné funkce je následující:
$$ f(x): y = x^n $$
kde x je nezávisle proměnná tak, jak ji známe z jiných druhů funkcí a n je exponent neboli mocnitel. Exponent určuje, na kolikátou musíme nějaké číslo (tzv. základ mocniny) – v našem případě hodnotu nezávisle proměnné x – umocnit, abychom dostali výsledek – v našem případě hodnotu závisle proměnné y.
Rozlišujeme dva základní druhy mocninných funkcí:
- mocninné funkce s přirozeným exponentem,
- mocninné funkce s celým exponentem.
U mocninné funkce s přirozeným exponentem patří exponent do oboru přirozených čísel, což jsou celá kladná čísla (1, 2, 3, 4, 5 atd.), zatímco mocninné funkce s celým exponentem rozšiřují množinu možných exponentů o číslo 0 a celá záporná čísla (-1, -2, -3, -4, -5 atd.)
Aby toho nebylo najednou moc, rozdělíme mocninné funkce do dvou článků – v tomto se budeme věnovat mocninným funkcím s přirozeným exponentem a v tom následujícím mocninným funkcím s celým exponentem.
Mocninné funkce s přirozeným exponentem
Dva druhy mocninných funkcí s přirozeným exponentem už jsme vlastně poznali z předchozích článků. Prvním je funkce s exponentem 1.
n = 1
Její předpis vypadá takto:
$$ f(x): y = x^1 \rightarrow f(x): y = x $$
Předpis $ y = x^1 $ jsme mohli zjednodušit na $ y = x $, protože když jakékoli číslo umocníme na prvou, je to stejné, jako bychom ho neumocnili vůbec. Tím pádem tato mocninná funkce s exponentem 1 je vlastně lineární funkce s koeficienty a = 1, b = 0. Jde tedy navíc o přímou úměrnost, takže jejím grafem je přímka procházející počátkem souřadného systému (bodem [0; 0]). Tato přímka je zároveň osou I. a III. kvadrantu:
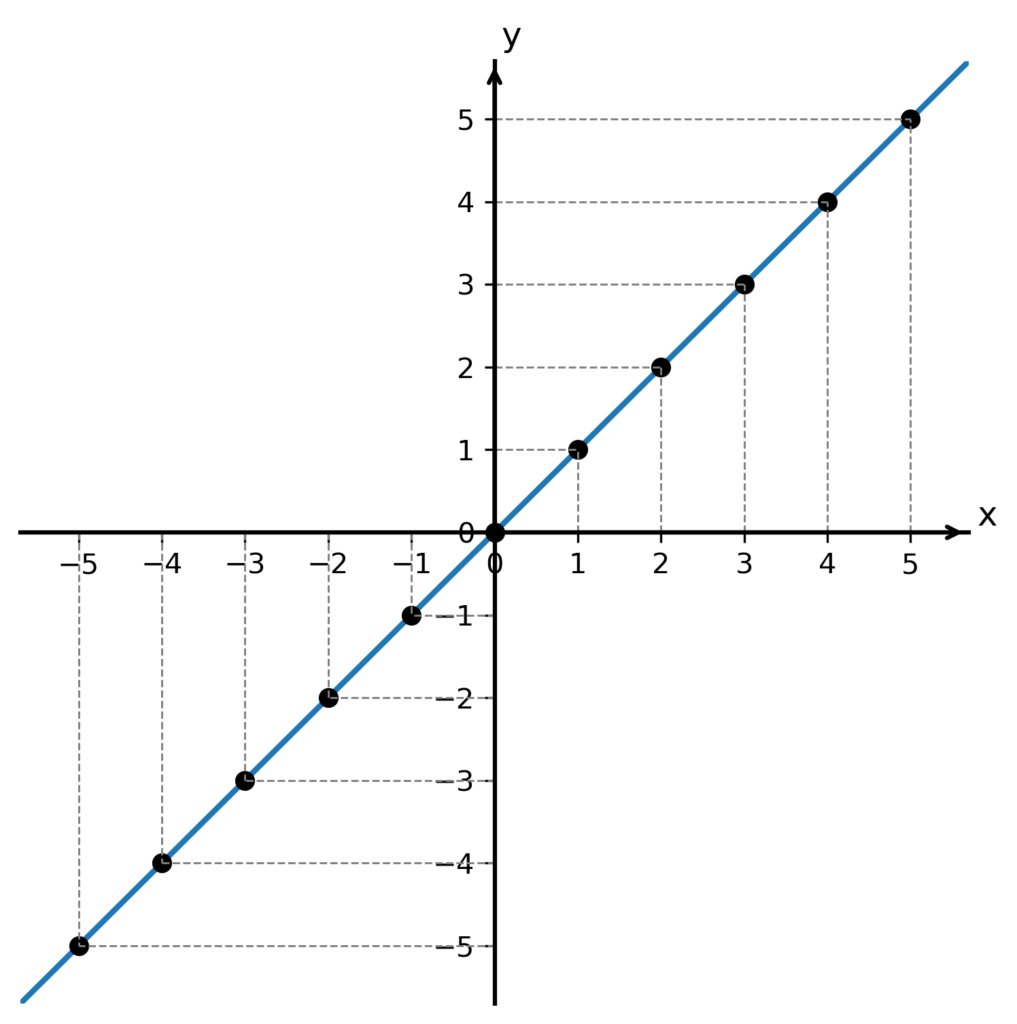
Myslím, že i z grafu je jasně patrné, že funkce s nezávisle proměnnou x „nic nedělá“ (nijak ji nepřepočítává). Zkrátka přiřadí závisle proměnné y právě tu hodnotu x, kterou do ní dosadíme.
Dodejme, že graf je středově souměrný podle počátku souřadného systému – funkce je tedy lichá.
n = 2
Druhou mocninnou funkcí, kterou už známe, je funkce s exponentem 2:
$$ f(x): y = x^2 $$
Jde o nejjednodušší kvadratickou funkci (bez lineárního a absolutního členu a s koeficientem a = 1). Jejím grafem je tedy parabola s vrcholem v počátku souřadného systému:

Graf je osově souměrný podle osy y – funkce je tedy sudá.
n = 3
Pojďme nyní zvýšit náš exponent na hodnotu n = 3 a sestrojme si graf příslušné mocninné funkce:
$$ f(x): y = x^3 $$
Vytvořme si tabulku hodnot x a vypočítejme k nim příslušné hodnoty y:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -8 | -1 | 0 | 1 | 8 |
Graf bude vypadat následovně:
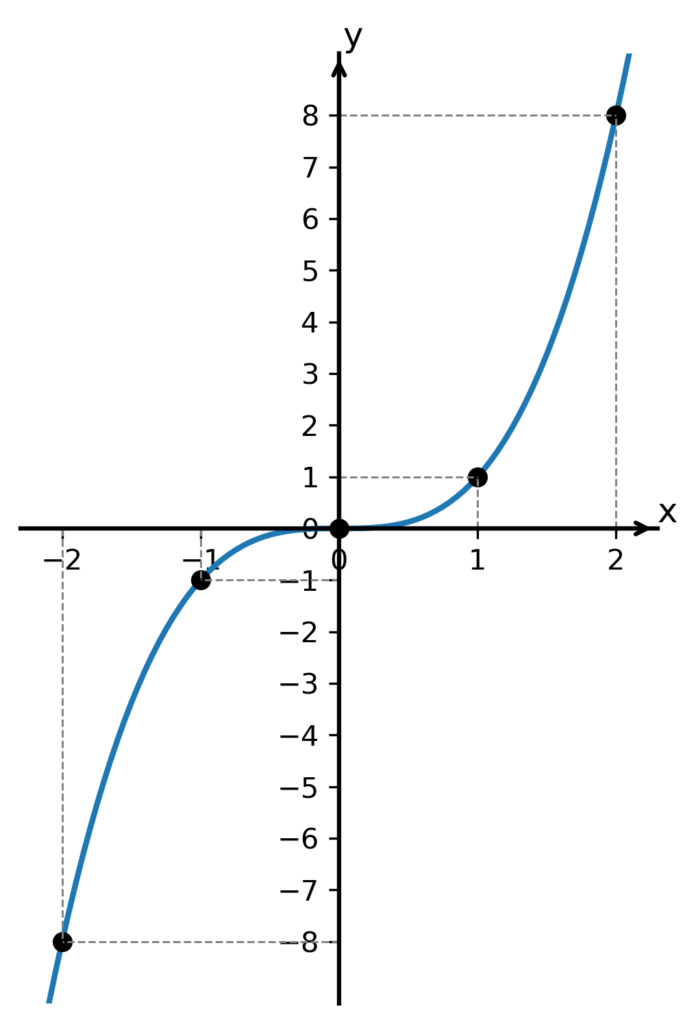
Grafem této funkce $ y = x^3 $ je parabola třetího stupně. (Kolikátého stupně parabola je, určuje právě exponent n. Pro n = 2 nemusíme říkat „parabola druhého stupně“, ale jen „parabola“, protože „obyčejnou“ parabolou – bez přívlastku – se myslí právě parabola druhého stupně.)
Parabola třetího stupně je „strmější“ než parabola nižšího stupně. Např. číslo 2 na druhou se rovná 4, ale 2 na třetí je už 8. Obecně platí, že čím vyšší bude náš exponent n v předpisu funkce, tím bude parabola „strmější“ (kromě intervalu hodnot $ x \in \langle -1; 1 \rangle $, ale to teď zanedbejme).
Navíc zde vidíme další významnou vlastnost – naše parabola třetího stupně už není osově souměrná jako „klasická“ parabola (tedy parabola druhého stupně), ale má zápornou větev ve III. kvadrantu souřadného systému. Místo toho je středově souměrná podle počátku tohoto souřadného systému – funkce je tedy lichá.
Je to dáno tím, že např. číslo -2 umocněné na druhou je $ (-2) \cdot (-2) = 4 $, tedy stejně jako +2 umocněné na druhou. Zkrátka ať dosadíme do funkce $ y = x^2 $ záporné nebo kladné číslo, výsledek bude vždycky kladný. Ale číslo -2 umocněné na třetí je $ (-2) \cdot (-2) \cdot (-2) = -8 $, čili když dosadíme do funkce $ y = x^3 $ záporné číslo, výsledek bude vždy záporný.
n = 4
Uveďme si ještě graf mocninné funkce pro hodnotu exponentu n = 4, tedy pro funkci:
$$ f(x): y = x^4 $$
Opět si vytvoříme tabulku hodnot x a k nim příslušných hodnot y:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 16 | 1 | 0 | 1 | 16 |
Graf bude vypadat následovně:
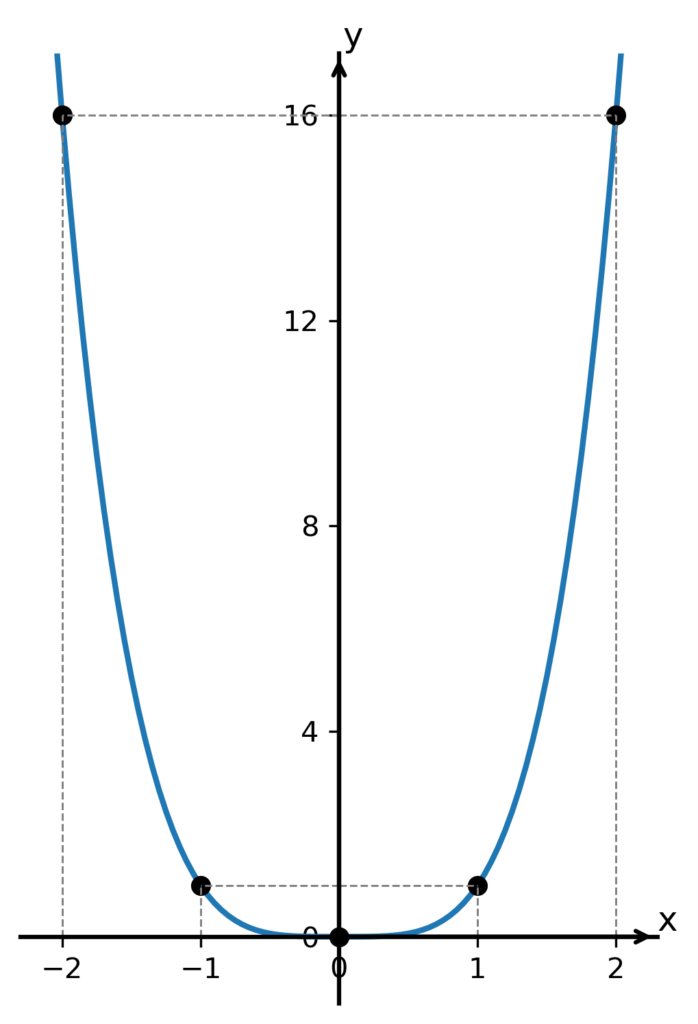
Graf tvoří parabola čtvrtého stupně. Vidíme, že je souměrný podle osy y a funkce je tedy sudá.
Vlastnosti mocninných funkcí s přirozeným exponentem
Možná jste si všimli, že pokud máme v předpisu funkce lichý exponent (1, 3 apod.), funkce je lichá, a naopak – pokud máme v předpisu funkce sudý exponent (2, 4 apod.), funkce je sudá. Je tomu skutečně tak a platí to obecně pro libovolný přirozený lichý, resp. sudý, exponent.
Definičním oborem každé mocninné funkce s přirozeným exponentem je množina všech reálných čísel, tedy platí:
$$ D(f) = R $$
Obor hodnot i další vlastnosti mocninné funkce s přirozeným exponentem opět záleží na tom, je-li tento exponent lichý nebo sudý. Pojďme si tyto vlastnosti shrnout.
Je-li exponent lichý:
- Příslušná parabola n-tého stupně má zápornou větev ve III. kvadrantu souřadného systému a jejím oborem hodnot jsou díky tomu všechna reálná čísla, tedy platí $ H(f) = R $.
- Je rostoucí.
- Je lichá.
- Není ani shora ani zdola omezená.
- Nemá v žádném bodě ani minimum ani maximum.
Je-li exponent sudý:
- Příslušná parabola n-tého stupně nemá zápornou větev ve III. kvadrantu souřadného systému, a její obor hodnot je díky tomu omezený pouze na nezáporná čísla, tedy platí $ H(f) = \langle 0; +\infty) $.
- Je klesající na intervalu $ (-\infty; 0 \rangle $ a rostoucí na intervalu $ \langle 0; +\infty) $.
- Je sudá.
- Je zdola omezená.
- V bodě x = 0 má minimum, v žádném bodě nemá maximum.
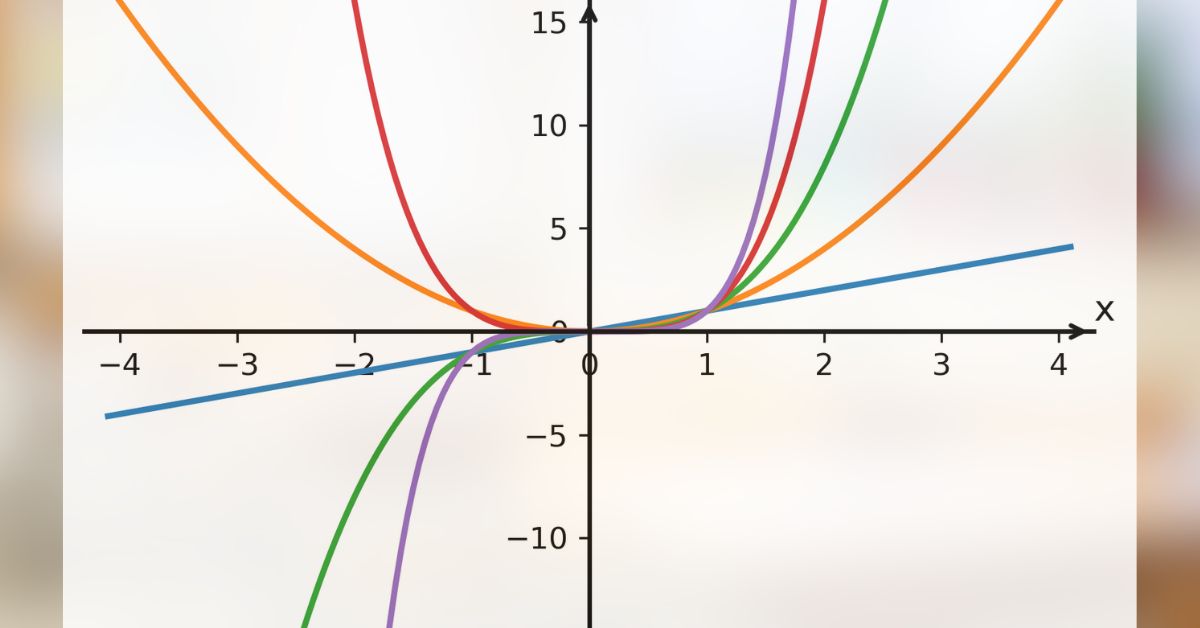
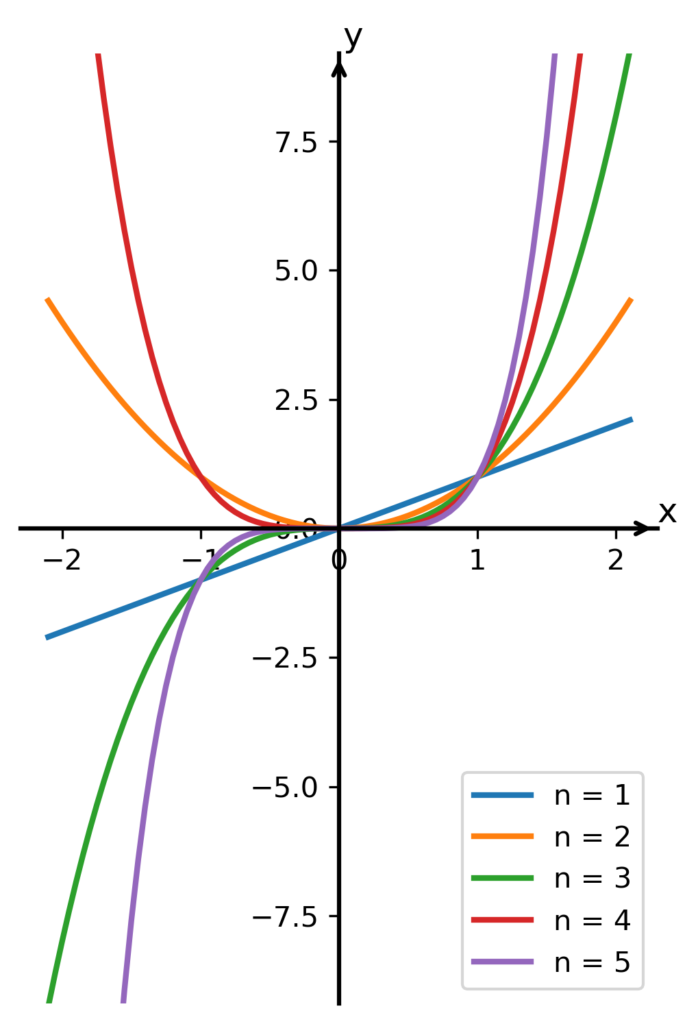
Ukažme si na závěr ještě jeden obrázek s grafy několika mocninných funkcí s přirozeným exponentem zakreslenými do jednoho souřadného systému, aby byly jednotlivé vlastnosti těchto funkcí názornější.
Závěr
V tomto článku jsme se podívali na mocninné funkce s přirozeným exponentem. V následujícím článku se budeme věnovat mocninným funkcím s celým exponentem. Protože přirozená čísla rovněž patří mezi čísla celá, a příslušným mocninným funkcím jsme se věnovali v tomto článku, konkrétně se budeme zabývat mocninnými funkcemi, kde je tento exponent záporný nebo nulový.