V předchozích dvou článcích jsme si vysvětlili, co jsou logaritmy, což nám poskytlo znalosti potřebné k tomu, abychom se v tomto článku mohli věnovat logaritmické funkci.
Je to poslední druh funkce ze všech hlavních druhů funkcí, které se probírají na středních školách. Resp. do středoškolského učiva patří ještě goniometrické funkce (sinus, kosinus, tangens, kotangens), které se ale obvykle vyučují v samostatném celku jakožto součást goniometrie.
Definice a obecný předpis logaritmické funkce
Logaritmická funkce o základu a je inverzní funkce k exponenciální funkci o témže základu a. Její obecný předpis vypadá následovně:
$$ f(x): y = \log_a x $$
Výraz $ \log_a x $ čteme jako „logaritmus x o základu a“ nebo „logaritmus o základu a čísla x“.
Tato definice může vypadat poněkud vágně, ale logaritmická funkce je skutečně definována jako inverzní funkce k exponenciální funkci – žádná jiná „věda“ za tím není.
Platí zde samozřejmě stejné podmínky, které jsme uvedli v předchozím článku o logaritmech jako takových, tedy:
- Základ logaritmu a musí být kladné číslo kromě čísla 1.
- Proměnná x musí být kladné číslo.
Z 2. podmínky plyne definiční obor logaritmické funkce, který můžeme zapsat takto:
$$ D(f) = (0; +\infty) $$
Graf logaritmické funkce
Graf logaritmické funkce se nazývá logaritmická křivka.
Zvolme základ logaritmu a = 2, vytvoříme tabulku několika hodnot x a vypočítáme k nim příslušné hodnoty y – to znamená, že každé číslo x zlogaritmujeme:
| x | $ \frac{1}{8} $ | $ \frac{1}{4} $ | $ \frac{1}{2} $ | 1 | 2 | 4 | 8 |
| y | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
První tři hodnoty x jsme záměrně zvolili tak, aby ve výsledném obrázku byla vidět i „záporná větev“ logaritmické křivky, kterou v tomto případě získáme pro ta čísla x, která jsou menší než 1.
Graf této logaritmické funkce vypadá následovně:

Nyní zvolíme základ logaritmu $ a = \frac{1}{2} $ a opět vytvoříme tabulku hodnot x a k nim příslušných hodnot y:
| x | $ \frac{1}{8} $ | $ \frac{1}{4} $ | $ \frac{1}{2} $ | 1 | 2 | 4 | 8 |
| y | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
A sestrojíme graf:

Z obou obrázků je patrné, že obdobně jako u exponenciální funkce i zde platí, že je-li základ logaritmu a menší než 1 (ale stále musí být větší než 0), graf funkce bude klesající, a je-li základ logaritmu a větší než 1, graf funkce bude rostoucí.
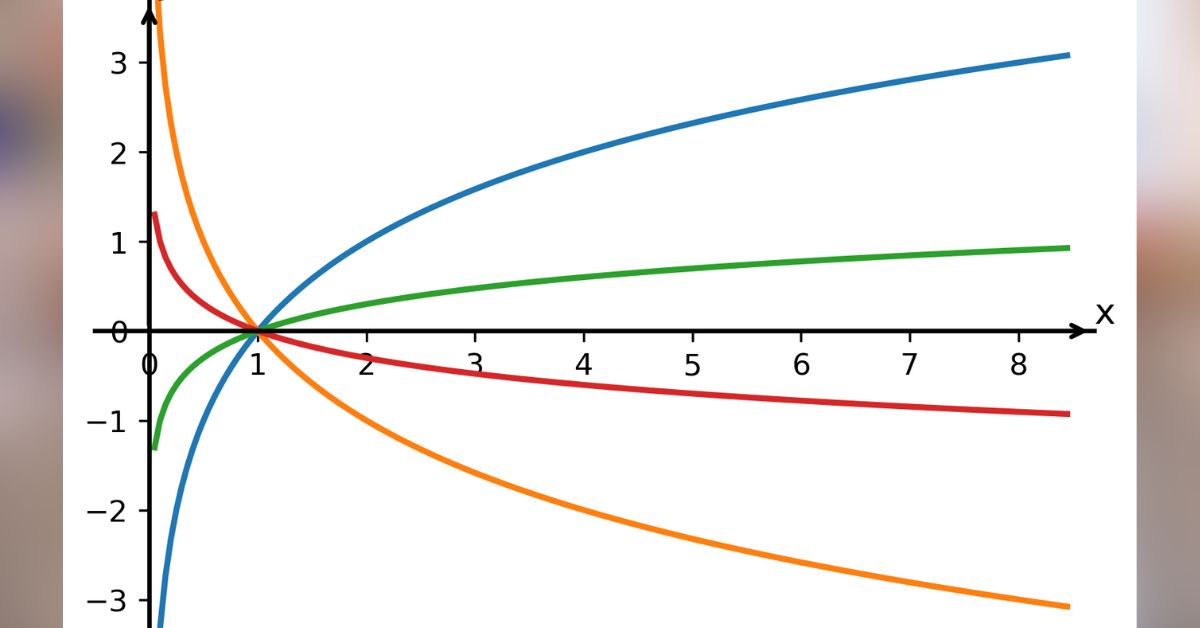
Navíc platí, že pokud máme dvě různé logaritmické funkce se základy, které tvoří čísla vzájemně převrácená, což je i náš případ, grafy těchto funkcí budou osově souměrné podle osy x. Ukažme si to na následujícím obrázku, který obsahuje grafy obou výše uvedených funkcí zakreslených do jednoho souřadného systému:

Abychom lépe ilustrovali skutečnost, že logaritmická funkce je inverzní k exponenciální funkci, ukažme si ještě dva obrázky, na kterých je vidět, že pokud máme osy souřadného systému ve stejně velkých jednotkách, grafy obou funkcí budou osově souměrné podle osy I. a III. kvadrantu.
Graf exponenciální funkce $ y = 2^x $ a k ní inverzní logaritmické funkce $ y = \log_2 x $:

Graf exponenciální funkce $ y = \big(\frac{1}{2}\big)^x $ a k ní inverzní logaritmické funkce $ y = \log_{\frac{1}{2}} x $:

Speciální druhy logaritmických funkcí
Pokud je základ logaritmu a = 10, funkce se nazývá dekadická logaritmická funkce, která se značí následovně:
$$ f(x): y = \log x $$
To znamená, že se u zápisu „log“ v dolním indexu neuvádí její základ. Nebo opačně můžeme říci, že není-li u logaritmické funkce uveden její základ, jedná se automaticky o dekadickou logaritmickou funkce se základem 10.
A pokud je základ logaritmu a = e (Eulerovo číslo), funkce se nazývá přirozená logaritmická funkce, a značí se takto:
$$ f(x): y = \ln x $$
Vlastnosti logaritmické funkce
Shrňme si specifické vlastnosti logaritmické funkce:
- Definiční obor je $ D(f) = (0; +\infty) $.
- Obor hodnot je $ H(f) = R $.
- Pokud je hodnota koeficientu a větší než 0, ale menší než 1, funkce je klesající.
- Pokud je hodnota koeficientu a větší než 1, funkce je rostoucí.
- Je prostá.
- Není ani zdola ani shora omezená.
- Nemá v žádném bodě ani minimum ani maximum.
- Funkční hodnota v bodě x = 1 je vždy rovna 0, což znamená, že graf každé logaritmické funkce prochází bodem o souřadnicích [1; 0].
Závěr
V tomto článku jsme probrali logaritmickou funkci, což je poslední funkce z kolekce funkcí (kromě goniometrických funkcí, jež patří do samostatného oddílu), které se vyučují na střední škole. Pokud jste si prostudovali všechny články v této kategorii, máte pevně osvojené základy celé jedné oblasti matematiky. Gratuluji, že jste došli až sem!