V předchozím článku jsme si řekli, co je to funkce a jaká existují pojetí její definice.
V tomto článku si vysvětlíme, co je graf funkce, definiční obor funkce, co znamená, když se řekne „hodnota funkce v bodě“ a další související termíny.
Vraťme se k našemu příkladu z minulého článku, kdy jsme definovali funkci udávající závislost doby volného pádu na výšce, ze které těleso padá. Tato funkce měla následující předpis:
$$ y = \sqrt{\frac{2x}{9,81}} $$
Můžeme do ní dosadit za x výšku v metrech a pomocí jejího předpisu si spočítat y, což je doba volného pádu z této výšky v sekundách. Pokud za x dosadíme např. číslo 10, vyjde nám y zhruba 1,43. To znamená, že když pustíme např. kámen z výšky 10 metrů, bude trvat asi 1,43 sekundy, než dopadne na zem. Potom si můžeme za x dosadit např. číslo 20 a vyjde nám y zhruba 2,02. Zkrátka si za x můžeme dosadit jakoukoli nezápornou hodnotu a vždy nám vyjde příslušné y.
Definiční obor funkce
Právě jsem použil pojem „jakoukoli nezápornou hodnotu“, což znamená že výška, za které kámen pouštíme, musí být rovna nebo větší než 0. A právě tahle podmínka určuje definiční obor naší funkce.
Definiční obor funkce f značíme jako D(f) a je to množina všech čísel, které můžeme do funkce dosadit jakožto hodnoty x tak, že k těmto hodnotám existují hodnoty y, které jim předpis funkce přiřazuje.
Jinými slovy do definičního oboru patří taková čísla x, která můžeme do předpisu funkce „bezpečně“ dosadit, aby bylo možné vypočítat příslušné y. To znamená, že nedojde k žádné „zakázané operaci“, jako např. dělení nulou a podobně.
V případě naší funkce:
$$ f(x) = \sqrt{\frac{2x}{9,81}} $$
vidíme, že výraz obsahující x je celý pod druhou odmocninou. A druhá odmocnina ze záporných čísel neexistuje (alespoň ne v oboru reálných čísel). Proto nemůžeme do funkce dosadit např. hodnotu -10. Nejmenší možná hodnota, ze které jde spočítat druhá odmocnina, je číslo 0. V případě volného pádu by takový výpočet ani neměl smysl, protože nemůžeme pouštět předměty ze záporných výšek.
Dobře, dospěli jsme k závěru, že interval čísel, které je možné do funkce dosadit, abychom dostali „rozumný“ výsledek, začíná v čísle 0. Ale kde tento rozsah končí? Největší hodnota neexistuje, protože druhou odmocninu můžeme spočítat z libovolného nezáporného čísla, což znamená, že tento interval může pokračovat do nekonečna.
Takže cokoli mezi nulou a nekonečnem je možné do předpisu naší funkce dosadit, aby tento předpis fungoval. Můžeme tedy zapsat definiční obor naší funkce jako interval od nuly (včetně) až plus nekonečno:
$$ D(f) = \langle 0; +\infty) $$
Takto získanému definičnímu oboru se někdy říká maximální definiční obor, protože je daný pouze matematickými pravidly. Nic se nestane, dosadíme-li do předpisu funkce např. číslo 100 000 000 (metrů, což je 100 000 kilometrů), stále nám vyjde nějaké číslo y.
Ve skutečnosti ale pro takto vysokou hodnotu už naše funkce nebude dávat přesné výsledky, protože gravitace v takové vzdálenosti od Země je již mnohem slabší.
Navíc my sami si můžeme stanovit, že maximální výška, pro kterou budeme počítat dobu volného pádu, bude třeba „jen“ 500 metrů.
Ať už bude maximální hodnota určena „rozumnou výškou“, pro kterou bude předpis naší funkce fungovat dostatečně přesně, nebo námi samými, znamená to, že si také sami můžeme stanovit (omezit) definiční obor funkce.
Rozhodneme-li se, že funkci budeme potřebovat pouze do maximální výšky 500 metrů, pak náš definiční obor bude dán intervalem od 0 (včetně) do 500 (včetně):
$$ D(f) = \langle 0; 500 \rangle $$
Graf funkce
Máme tedy funkci definovanou předpisem:
$$ f(x) = \sqrt{\frac{2x}{9,81}} $$
a s definičním oborem:
$$ D(f) = \langle 0; 500 \rangle $$
Nyní si do předpisu funkce můžeme za x dosazovat libovolná čísla z našeho definičního oboru a vždy nám vyjde příslušné y.
My bychom ale rádi viděli, jaké hodnoty y dostaneme pro všechny možné hodnoty x z našeho intervalu (definičního oboru funkce), abychom si o chování funkce udělali ucelenější představu. A právě k tomu slouží graf funkce.
Graf naší funkce získáme např. tak, že si nejdříve uděláme tabulku čísel x s odstupňovanými hodnotami třeba po sto metrech, ke každé této hodnotě spočítáme příslušnou hodnotu y (s přesností třeba na setiny sekundy), potom si každou takto získanou dvojici nakreslíme jako puntík do souřadného systému, a nakonec proložíme tyto body křivkou.
Tabulka bude vypadat takto:
| x | 0 | 100 | 200 | 300 | 400 | 500 |
| y | 0 | 4,52 | 6,39 | 7,82 | 9,03 | 10,10 |
A vlastní graf pak následovně:
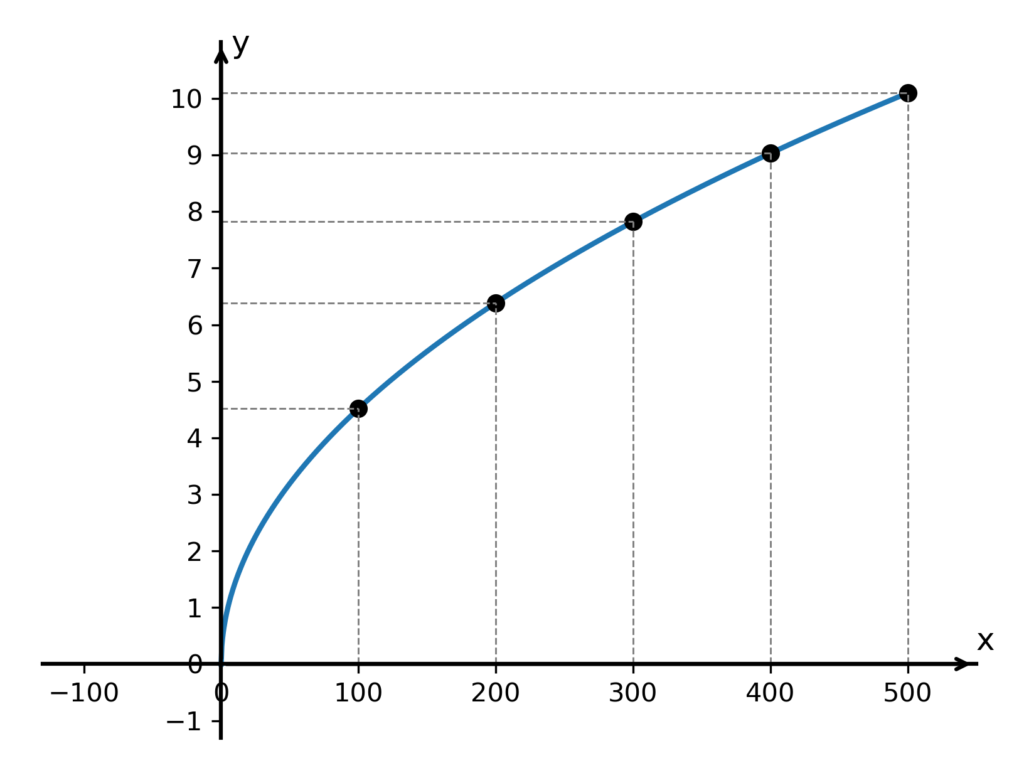
Vidíme, že nám vznikla krásná hladká křivka, což je v tomto případě jedna větev paraboly „položené naležato“. Také vidíme, že hodnoty funkce y rostou napřed rychle, potom pomaleji, ale stále rostou. To je logické, protože budeme-li pouštět těleso z určité výšky, jeho rychlost bude konstantně růst od nuly a prvních 100 metrů pádu tím pádem bude trvat déle, ale rozdíl mezi 100 a 200 metry už překoná za kratší dobu, protože tento úsek překoná již značně vyšší rychlostí, rozdíl od 200 do 300 metrů překoná ještě rychleji, takže přírůstek času bude ještě menší atd.
Dále vidíme, že křivka začíná v bodě [0; 0] a nevyskytuje se ani pod osou x ani na levé straně osy y, a končí právě u hodnoty 500, což je v souladu s definičním oborem. Zkrátka na první pohled vidíme spoustu vlastností funkce, které bychom pouze z jejího předpisu neviděli, a máme o ní mnohem jasnější představu.
Pojem graf funkce musíme ještě trochu upřesnit. Ve volnějším významu se jím myslí celý obrázek, tzn. osy x a y s na nich vynesenými hodnotami a popisky (tj. souřadný systém), body reprezentující souřadnice ze sloupců naší tabulky, a pak vlastní křivku grafu funkce.
Ve striktnějším významu grafem funkce f nazýváme množinu všech bodů [x, y], roviny Oxy, jejichž pravoúhlé souřadnice jsou sobě přiřazené hodnoty proměnné x a funkční hodnoty y = f(x).
To znamená, že se jím myslí v podstatě jen všechny body, které tvoří danou křivku. Proto můžeme říci, že např. grafem nějaké funkce je přímka nebo parabola či hyperbola a podobně.
Důležitý dodatek k definici funkce, který úzce souvisí s jejím grafem
Jak jsme si uvedli v předchozím článku, funkce představuje jednoznačné přiřazení hodnoty y nějaké hodnotě x. To znamená, že funkce přiřazuje každé hodnotě x z jejího definičního oboru právě jednu hodnotu y, nikdy ne více. Nemůžeme do funkce dosadit nějaké číslo a jako výsledek získat čísla dvě nebo více.
S tím souvisí i graf funkce. Abychom o nějakém grafu mohli říci, že je grafem funkce, musí tuto podmínku splňovat. Když si zvolíme libovolné číslo na ose x, které patří do definičního oboru funkce, a potom se budeme dívat směrem od tohoto čísla kolmo vzhůru nebo kolmo dolů, musíme vždy narazit právě na jeden bod, který leží na příslušné křivce.
Příkladem grafu, který není grafem funkce, může být například parabola „položená na ležato“. Viz následující obrázek:

Zde, ať se podíváme na jakoukoli hodnotu na ose x, která patří do definičního oboru, což jsou čísla v intervalu:
$$ \langle 0; +\infty \rangle $$
tak s výjimkou čísla 0 vidíme, že mu přísluší hned dvě hodnoty y. Například k číslu x = 16, najdeme hodnotu y = 4, ale také y = -4. Proto se sice jedná o graf paraboly, který bychom mohli sestrojit například v analytické geometrii, ale rozhodně se nejedná o graf funkce.
Hodnota funkce v bodě
V teorii a příkladech týkajících se funkcí se často setkáte s pojmem „hodnota funkce v bodě“ nebo také „funkční hodnota funkce f v bodě (čísle)“. Hodnotou funkce v bobě se rozumí výsledné číslo y odpovídající konkrétnímu číslu x. V tomto pojetí se tedy nejedná o bod v nějakém souřadném systému, ale skutečně jen o číslo, které do funkce dosadíme.
Protože, jak jsem právě napsal, se jedná o konkrétní hodnoty x a y, značí se zpravidla x0 a y0. Rozumí se tím, že když do předpisu funkce dosadíme jedno konkrétní číslo x0 ze všech možných hodnot x, dostaneme ze všech možných hodnot y jednu konkrétní hodnotu y0.
Symbolicky se tento vztah značí následujícím způsobem:
$$ f(x_0) = y_0 $$
Například u naší funkce týkající se volného pádu bychom mohli říci, že hodnota funkce v bodě x0 = 100 je 4,52 (viz tabulka výše).
Symbolicky to zapíšeme takto:
$$ f(100) = 4,52 $$
Obdobně pro jiné vybrané hodnoty x0:
$$ f(200) = 6,39 $$
$$ f(300) = 7,82 $$
Zde zase říkáme, že hodnota funkce v bodě 200 je 6,39 a v bodě 300 pak 7,82. Což v překladu znamená, že dosadíme-li do předpisu funkce za x hodnotu 200, vyjde nám hodnota y = 6,39, a dosadíme-li do předpisu funkce za x hodnotu 300, vyjde nám hodnota y = 7,82.
Záměrně na tento pojem upozorňuji, protože to často působí zmatek. Když se řekne „bod“, člověk si zpravidla představí bod ležící někde v rovině nebo prostoru, ale zde se bodem myslí zkrátka jen konkrétní hodnota x.
V následujícím článku se podíváme na specifické vlastnosti funkcí.


