V předchozím článku jsme se věnovali funkci n-tá odmocnina. Nyní nás čekají ještě dva důležité druhy funkcí – exponenciální a logaritmická, které jsou vzájemně inverzní.
V tomto článku se podíváme na exponenciální funkci.
Obecný předpis exponenciální funkce
Exponenciální funkce je definována následujícím předpisem:
$$ f(x): y = a^x $$
kde a je pevně dané číslo, kterému říkáme základ mocniny, a x je nezávisle proměnná funkce, tak jak ji známe z jiných druhů funkcí.
V jednom z minulých článků jsme probírali mocninné funkce typu $ y = x^n $, kde x byla proměnná a n pevně zvolené číslo (exponent). Proměnnou x jsme tedy umocňovali pevně daným exponentem.
Nyní jsme v trochu jiné jakoby opačné situaci: pevně dané číslo umocňujeme proměnnou x. Tento rozdíl je třeba mít na zřeteli, aby se nám exponenciální funkce nepletla s mocninnou funkcí.
Vraťme se ale k exponenciální funkci. Proměnnou x tedy nemáme v základu mocniny, ale v exponentu.
Z minulých článků víme, že určité číslo můžeme umocnit například na druhou, na třetí, na čtvrtou, ale také na nultou, na minus prvou, na minus druhou atd. Zkrátka jsme čísla umocňovali celočíselným exponentem. Jenže proměnná x může nabývat jakýchkoli hodnot, které nemusí patřit mezi celá čísla. A tak vzniká otázka, zda je vůbec možné umocnit nějaké číslo exponentem např. 2,5 nebo jakýmkoli jiným desetinným číslem.
Odpověď zní ano, je to možné. Jaký je za tím princip si necháme do jiného článku, ale vaše kalkulačka konkrétní číslo neceločíselným exponentem bez problémů umocní. Avšak existuje jedno omezení: neceločíselnými exponenty můžete umocňovat pouze kladná čísla. A z toho plyne první podmínka pro předpis exponenciální funkce: Základ mocniny – číslo a – musí být kladné.
Další podmínkou je, že toto číslo a se nesmí rovnat jedné. Kdyby se základ mocniny a rovnal jedné, sice by nedošlo k žádné „zakázané operaci“, jako např. dělení nulou, ale když jedničku umocníme libovolným číslem, výsledek bude stále jedna, takže z naší funkce by se stala funkce konstantní s předpisem $ y = 1 $, kterou už bychom nemohli nazvat exponenciální.
Číslo a tedy může být menší než 1 nebo větší než 1, ale každopádně musí být kladné. To znamená, že musí patřit do jednoho z intervalů $ (0; 1) $ nebo $ (1; +\infty) $. Podle toho, který z těchto dvou intervalů to bude, pak bude funkce buď klesající nebo rostoucí, jak uvidíme dále.
Graf exponenciální funkce
Zvolme základ mocniny a = 2 a získáme tak funkci s předpisem:
$$ f(x): y = 2^x $$
Dále si uděláme tabulku pro několik čísel x a spočítáme odpovídající hodnoty y. Zvolíme celá čísla x, protože těmi umocňovat umíme:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | $ \frac{1}{8} $ | $ \frac{1}{4} $ | $ \frac{1}{2} $ | 1 | 2 | 4 | 8 |
Pokud vám není jasné, jak jsme tyto hodnoty spočítali, tak zde je krátká rekapitulace:
Asi je zřejmé, že $ 2^1 = 2 $, $ 2^2 = 4 $ a $ 2^3 = 8 $ (pravá část tabulky). Dále víme, že jakékoli číslo umocněné na nultou je 1 (prostřední sloupec tabulky). A zápornými exponenty se umocňuje tak, že dané číslo (v našem případě 2) dáme do jmenovatele zlomku, v jehož čitateli je jednička, a umocníme ho exponentem kladným. Takže:
$ 2^{-1} = \frac{1}{2^1} = \frac{1}{2} $,
$ 2^{-2} = \frac{1}{2^2} = \frac{1}{4} $ a
$ 2^{-3} = \frac{1}{2^3} = \frac{1}{8} $
(levá část tabulky).
Body dané sloupci tabulky si můžeme vynést do souřadného systému, proložit jimi křivku a získáme graf:
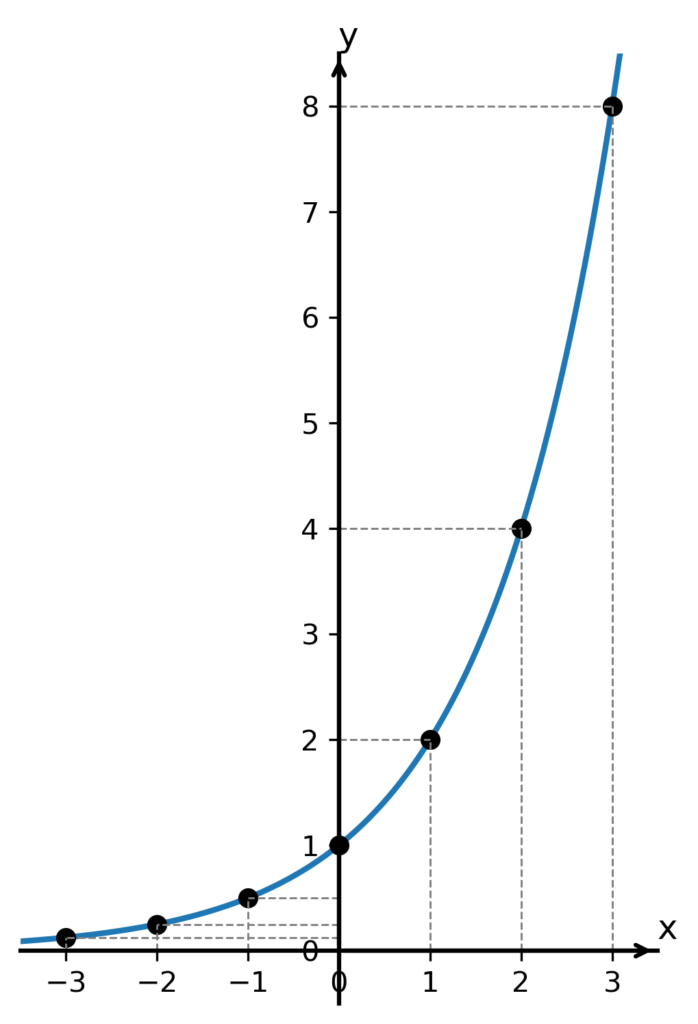
Grafem funkce je exponenciální křivka.
Vidíme, že exponenciální křivka v tomto našem případě zpočátku (pro záporné hodnoty x) roste velmi pozvolna, v bodě x = 0 se dostane na hodnotu y = 1, a dále roste stále strměji.
Exponenciální funkce je velmi mocná – ve svém růstu překoná kvadratickou i každou jinou mocninnou funkci s přirozeným exponentem. Platí pro ni, že vždy, když zvětšíme proměnnou x o jedničku, funkční hodnota y se zvětší tolikrát, kolik činí hodnota koeficientu a – v našem případě tedy dvakrát.
Nyní si zvolme koeficient $ a = \frac{1}{2} $. Získáme tak exponenciální funkci s předpisem:
$$ f(x): y = \bigg(\frac{1}{2}\bigg)^x $$
Opět si uděláme tabulku dvojic hodnot x a y:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 8 | 4 | 2 | 1 | $ \frac{1}{2} $ | $ \frac{1}{4} $ | $ \frac{1}{8} $ |
a sestrojíme graf:
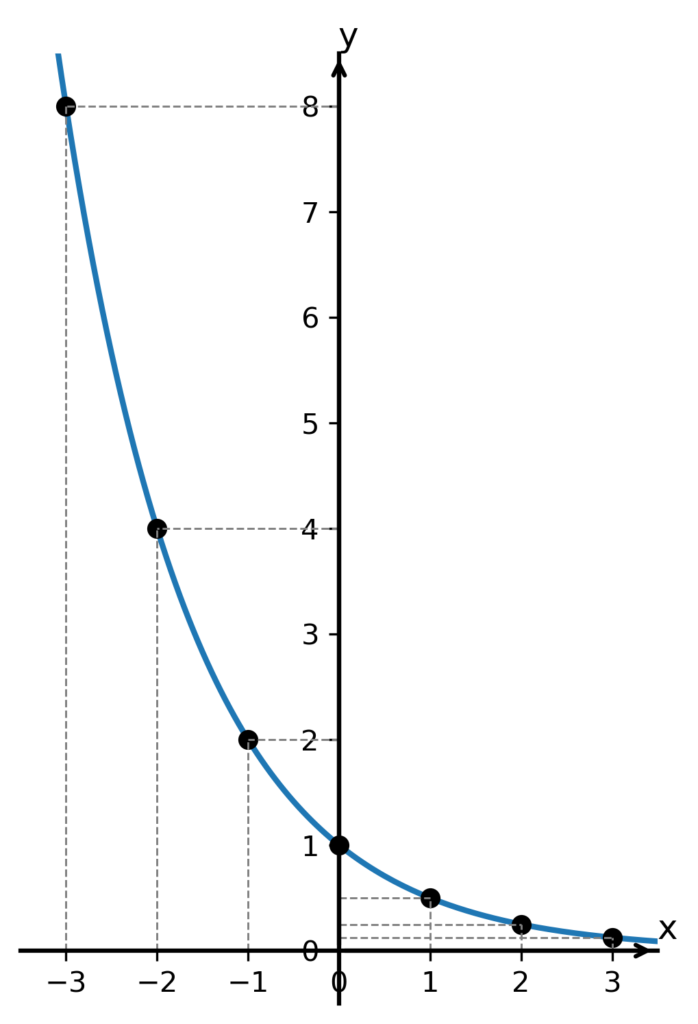
V tomto případě je naše funkce klesající. Pro záporné hodnoty x klesá velmi rychle, v bodě x = 0 se dostane na hodnotu y = 1, a dále klesá stále pozvolněji – blíží se k ose x, ale nikdy jí nedosáhne. I zde platí, že vždy když zvětšíme proměnnou x o jedničku, funkční hodnota y se změní tolikrát, kolik činí hodnota koeficientu a. Ta je v našem případě $ \frac{1}{2} $, takže funkční hodnota se tentokrát vždy dvakrát zmenší.
Grafy dvou exponenciální funkcí, jejichž základy a tvoří čísla vzájemně převrácená, budou osově souměrné podle osy y. To je i náš případ výše uvedených funkcí, protože čísla 2 a $ \frac{1}{2} $ jsou vzájemně převrácené hodnoty. Můžeme to vidět na následujícím obrázku, který ukazuje grafy těchto funkcí ještě jednou, tentokrát zakreslené do jedné soustavy souřadnic:

Pro hodnotu koeficientu a = 10 se funkce nazývá dekadická exponenciální funkce a pro hodnotu koeficientu a = e (Eulerovo číslo – základ přirozených logaritmů, bude blíže popsáno v dalším článku) se funkce nazývá přirozená exponenciální funkce.
Obecně platí, že čím bude hodnota koeficientu a větší, resp. menší, než 1, tím bude mít exponenciální křivka strmější průběh. Ukažme si pro srovnání několik exponenciálních křivek v jednom souřadném systému s různými hodnotami koeficientu a:

Vlastnosti exponenciální funkce
Shrňme si nyní specifické vlastnosti exponenciální funkce:
- Definiční obor je $ D(f) = R $.
- Obor hodnot je $ H(f) = (0; +\infty) $ (číslo 0 do něj nepatří, protože funkce této hodnoty nikdy nedosáhne – proto je interval otevřený).
- Pokud je hodnota koeficientu a větší než 0, ale menší než 1, funkce je klesající.
- Pokud je hodnota koeficientu a větší než 1, funkce je rostoucí.
- Je prostá.
- Je zdola omezená, není shora omezená.
- Nemá v žádném bodě ani minimum ani maximum.
- Funkční hodnota v bodě x = 0 je vždy rovna 1, což znamená, že graf každé exponenciální funkce prochází bodem o souřadnicích [0; 1].
Závěr
Exponenciální funkce se často projevují ve světě kolem nás. Lze pomocí nich vyjádřit například růst určité živočišné (i lidské) nebo rostlinné populace, rozmnožování bakterií, složené úrokování, nebo třeba jadernou přeměnu radioaktivních látek.
V příštím článku se budeme věnovat logaritmům.


