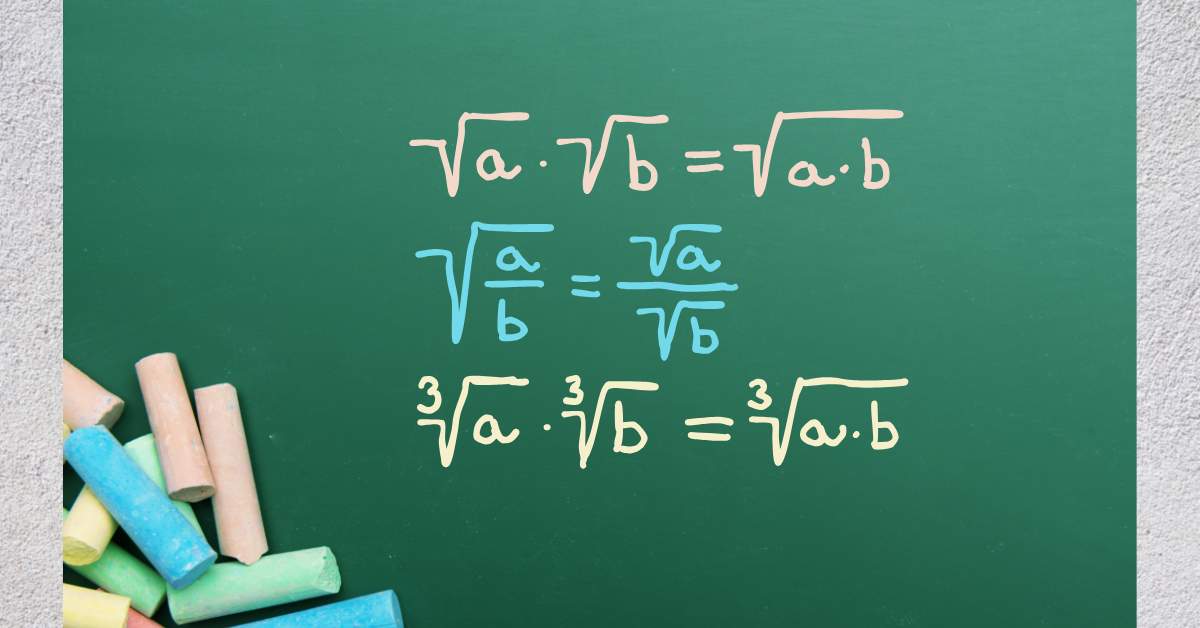Druhá a třetí odmocnina

V předchozím článku jsme se zabývali podmnožinami číselných oborů, a v článku ještě před ním číselnými obory jako takovými. Jako příklady iracionálních čísel zde byly uvedeny některé druhé odmocniny čísel.

V tomto článku se podíváme právě na odmocniny, konkrétně na druhou a třetí odmocninu reálného čísla.

Druhá odmocnina

Začneme definicí druhé odmocniny:

Druhá odmocnina z nezáporného reálného čísla a je takové nezáporné číslo x, pro které platí x² = a. K jeho označení užíváme symbol $ \sqrt{a} $.

$ \sqrt{\text{ }} $ je odmocnítko, a je základ odmocniny (odmocněnec).

Druhá odmocnina z nějakého čísla je tedy takové číslo, které když vynásobíme sebou samým (čili ho umocníme na druhou), tak dostaneme právě to číslo, ze kterého druhou odmocninu počítáme. Například:

$ \sqrt{9} = 3 $, protože $ 3 \cdot 3 = 3^2 = 9 $,

$ \sqrt{25} = 5 $, protože $ 5 \cdot 5 = 5^2 = 25 $,

$ \sqrt{64} = 8 $, protože $ 8 \cdot 8 = 8^2 = 64 $,

$ \sqrt{100} = 10 $, protože $ 10 \cdot 10 = 10^2 = 100 $ atd.

U druhé odmocniny je důležité mít na zřeteli dvě důležité věci, které jsou sice obsaženy v její definici, ale občas se na ně zapomíná:

1. Druhá odmocnina je definována pouze z nezáporného reálného čísla. To znamená, že druhé odmocniny ze záporných čísel, např. $ \sqrt{-5} $, $ \sqrt{-9} $ apod., nejsou v oboru reálných čísel definovány. Protože kdybychom si položili otázku jako třeba „Jaké číslo je potřeba vynásobit sebou samým (tedy umocnit ho na druhou), abychom dostali výsledek –9?“, tak na ni nenajdeme odpověď. Druhou odmocninu ze záporných čísel tedy počítat nelze, resp. lze to dělat až v oboru komplexních čísel, ale to je už jiná oblast matematiky, která nepatří do základních poznatků.
2. Druhá odmocnina z nezáporného čísla je vždy nezáporné číslo. Například $ \sqrt{4} = 2 $, přestože platí, že nejen $ 2^2 = 4 $, ale i $ (-2)^2 = 4 $, takže na otázku „Jaké číslo je třeba vynásobit sebou samým (tedy umocnit ho na druhou), abychom dostali výsledek 4?“ existují dvě odpovědi: 2 a –2. Jenže výsledek druhé odmocniny musí být jednoznačný, tzn. musí jím být právě jedno číslo, a proto je definice tohoto výsledku omezena na nezáporná čísla.

Užitečné vzorce pro počítání s druhými odmocninami

Užitečné vzorce pro počítání s druhými odmocninami shrnuje následující věta:

První vzorec můžeme použít pro odmocňování velkých čísel nebo pro tzv. částečné odmocňování. Také ho můžeme použít „druhým směrem“, kdy z tvaru odpovídajícímu jeho pravé straně vytvoříme tvar odpovídající jeho levé straně, abychom dostali číslo, které lze odmocnit jednoduše. Ukážeme si příklady:

Příklad 1

Vypočítejte:

a) $ \sqrt{8100} $, b) $ \sqrt{50} $, c) $ \sqrt{108} $, d) $ \sqrt{5} \cdot \sqrt{20} $.

Řešení

a)

\begin{align*} \sqrt{8100} &= \sqrt{81 \cdot 100} = \sqrt{81} \cdot \sqrt{100} = \\ &= 9 \cdot 10 = 90 \end{align*}

V tomto příkladu jsme si číslo 8100 rozložili na součin dvou menších čísel 81 a 100, z nichž každé lze odmocnit jednoduše. Toto použití prvního vzorce z rámečku výše se tedy hodí pro odmocňování velkých čísel, kde si nejsme jisti, jak bude vypadat výsledné číslo nebo kolik bude mít na konci nul.

b)

\[ \sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5 \cdot \sqrt{2} \]

Kdybychom spočítali druhou odmocninu z čísla 50 na kalkulačce, dostali bychom desetinné číslo s mnoha desetinnými místy (ve skutečnosti je těchto desetinných míst nekonečně mnoho), takže výsledek by byl zaokrouhlený nebo bychom ho my sami dále zaokrouhlili. Pokud chceme zachovat absolutní přesnost – třeba proto, že výsledek budeme někam dále dosazovat a nechceme, aby se nám akumulovaly zaokrouhlovací chyby – tak můžeme provést částečné odmocnění, jako jsme to udělali v tomto příkladu.

Částečné odmocnění znamená, že – pokud je to možné – si odmocňované číslo (odmocněnec) rozložíme na součin dvou čísel, z nichž jedno jde odmocnit jednoduše a přesně, tento součin rozdělíme podle prvního vzorce z rámečku výše na dvě odmocniny, první číslo odmocníme a druhé ponecháme zapsané jako odmocninu. Sice tím nedosáhneme toho, že bychom se druhé odmocniny z výsledku úplně zbavili, ale tento výsledek bude zapsán pomocí menších čísel, což může být přehlednější a současně nám to dá lepší představu, jak velké toto výsledné číslo je.

Ukážeme si ještě jeden příklad:

c)

\[ \sqrt{108} = \sqrt{36 \cdot 3} = \sqrt{36} \cdot \sqrt{3} = 6 \cdot \sqrt{3} \]

d)

\[ \sqrt{5} \cdot \sqrt{20} = \sqrt{5 \cdot 20} = \sqrt{100} = 10 \]

Zde jsme použili vzorec opačným směrem – ze součinu dvou odmocnin jsme si vytvořili odmocninu jednu, daná čísla jsme vynásobili a vypočítali jsme druhou odmocninu z tohoto násobku. Udělali jsme to proto, že ani číslo 5 ani číslo 20 nelze odmocnit přesně (druhá odmocnina každého z nich je desetinné číslo s nekonečným počtem desetinných míst), zatímco jejich součin odmocnit přesně lze.

Třetí vzorec z rámečku výše se používá pro odmocňování zlomků. Druhou odmocninu ze zlomku vypočítáme tak, že odmocníme zvlášť jeho čitatel a zvlášť jeho jmenovatel. Opět si ukážeme příklady:

Příklad 2

Vypočítejte:

a) $ \sqrt{\frac{4}{9}} $, b) $ \sqrt{\frac{16}{25}} $, c) $ \sqrt{\frac{49}{100}} $.

Řešení

a)

\[ \sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3} \]

b)

\[ \sqrt{\frac{16}{25}} = \frac{\sqrt{16}}{\sqrt{25}} = \frac{4}{5} \]

c)

\[ \sqrt{\frac{49}{100}} = \frac{\sqrt{49}}{\sqrt{100}} = \frac{7}{10} \]

Usměrňování zlomků

Zlomky, ve kterých se vyskytují odmocniny, je vhodné upravit tak, aby se žádné odmocniny nevyskytovaly v jejich jmenovatelích. Takový postup se nazývá usměrňování zlomků.

Usměrňování zlomků provádíme jejich rozšiřováním. Rozšíření zlomku je opakem krácení zlomku. Provedeme ho tak, že čitatel i jmenovatel daného zlomku vynásobíme týmž nenulovým číslem. Pokud chceme usměrnit zlomek, musíme najít vhodné číslo nebo číselný výraz, kterým zlomek rozšíříme, tak aby odmocnina nebo odmocniny z jeho jmenovatele zmizely.

Máme-li ve jmenovateli zlomku pouze jednu druhou odmocninu, rozšíříme zlomek stejnou druhou odmocninou – vynásobíme-li totiž dvě druhé odmocniny z daného čísla, jako výsledek dostaneme právě toto číslo. Například:

$$ \sqrt{2} \cdot \sqrt{2} = 2 $$

$$ \sqrt{5} \cdot \sqrt{5} = 5 $$

$$ \sqrt{10} \cdot \sqrt{10} = 10 $$

atd.

O tomto faktu se můžeme přesvědčit pomocí prvního vzorce z rámečku výše, např.:

\[ \sqrt{2} \cdot \sqrt{2} = \sqrt{2 \cdot 2} = \sqrt{4} = 2 \]

Budeme-li tedy mít ve jmenovateli zlomku druhou odmocninu ze dvou, rozšíříme zlomek právě druhou odmocninou ze dvou, budeme-li tam mít druhou odmocninu z jiného čísla, rozšíříme zlomek druhou odmocninou z tohoto čísla. Ukažme si příklady:

Příklad 3

Usměrněte zlomky:

a) $ \frac{6}{\sqrt{2}} $, b) $ \frac{4}{\sqrt{5}} $, c) $ \frac{5 \sqrt{6}}{\sqrt{10}} $, d) $ \frac{7 -\sqrt{7}}{\sqrt{7}} $, e) $ \frac{6 \sqrt{2} -4 \sqrt{6}}{\sqrt{8}} $.

Řešení

a)

\[ \frac{6}{\sqrt{2}} = \frac{6 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{6 \sqrt{2}}{2} = 3 \sqrt{2} \]

b)

\[ \frac{4}{\sqrt{5}} = \frac{4 \cdot \sqrt{5}}{\sqrt{5} \cdot \sqrt{5}} = \frac{4 \sqrt{5}}{5} \]

c)

\begin{align*} \frac{5 \sqrt{6}}{\sqrt{10}} &= \frac{5 \sqrt{6} \cdot \sqrt{10}}{\sqrt{10} \cdot \sqrt{10}} = \frac{5 \sqrt{60}}{10} = \frac{5 \sqrt{4 \cdot 15}}{10} = \\ &= \frac{5 \sqrt{4} \sqrt{15}}{10} = \frac{5 \cdot 2 \sqrt{15}}{10} = \frac{10 \sqrt{15}}{10} = \sqrt{15} \end{align*}

V tomto příkladu jsme použili první vzorec z rámečku výše k částečnému odmocnění čísla 60, což nám následně umožnilo zlomek vykrátit deseti.

d)

\begin{align*} \frac{7 -\sqrt{7}}{\sqrt{7}} &= \frac{(7 -\sqrt{7}) \cdot \sqrt{7}}{\sqrt{7} \cdot \sqrt{7}} = \frac{7 \sqrt{7} -7}{7} = \\ &= \frac{7(\sqrt{7} -1)}{7} = \sqrt{7} -1 \end{align*}

Zde jsme si v průběhu výpočtu v čitateli zlomku vytkli před závorku číslo 7, abychom ji mohli vykrátit se sedmičkou ve jmenovateli.

e)

\begin{align*} \frac{6 \sqrt{2} -4 \sqrt{6}}{\sqrt{8}} &= \frac{(6 \sqrt{2} -4\sqrt{6}) \cdot \sqrt{8}}{\sqrt{8} \cdot \sqrt{8}} = \frac{6 \sqrt{2} \sqrt{8} -4\sqrt{6} \sqrt{8}}{8} = \\ &= \frac{6 \sqrt{2 \cdot 8} -4 \sqrt{6 \cdot 8}}{8} = \frac{6 \sqrt{16} -4 \sqrt{48}}{8} = \\ &= \frac{6 \cdot 4 -4 \sqrt{16 \cdot 3}}{8} = \frac{24 -4 \sqrt{16} \sqrt{3}}{8} = \\ &= \frac{24 -4 \cdot 4 \sqrt{3}}{8} = \frac{24 -16 \sqrt{3}}{8} = \\ &= \frac{8(3 -2 \sqrt{3})}{8} = 3 -2 \sqrt{3} \end{align*}

U mnoha příkladů můžeme vidět, že usměrnění zlomku může vést až k výrazu, který žádný zlomek neobsahuje.

Ve jmenovateli zlomku však nemusíme mít jen jednu odmocninu, ale například dvojčlen. V takovém případě zlomek rozšíříme výrazem, který tento jmenovatel tvoří, pozměněným tak, že u druhého členu bude opačné znaménko. To nám umožní použít vzorec

$$ (A + B)(A -B) = A^2 -B^2 $$

Ukážeme si to na příkladech:

Příklad 4

Usměrněte zlomky:

a) $ \frac{2}{\sqrt{3} -1} $, b) $ \frac{3}{\sqrt{5} + \sqrt{2}} $.

Řešení

a)

\begin{align*} \frac{2}{\sqrt{3} -1} &= \frac{2}{\sqrt{3} -1} \cdot \frac{\sqrt{3} + 1}{\sqrt{3} + 1} = \frac{2(\sqrt{3} + 1)}{3 -1} = \\ &= \frac{2(\sqrt{3} -1)}{2} = \sqrt{3} + 1 \end{align*}

Jmenovatel původního zlomku $ \sqrt{3} -1 $ si můžeme představit jako závorku (A – B) z výše uvedeného vzorce. Tento výraz vynásobíme obdobou závorky (A + B) ze vzorce, tedy výrazem $ \sqrt{3} + 1 $. Výsledkem vzorce je výraz $ A^2 -B^2 $. Členu A ve vzorci odpovídá číslo $ \sqrt{3} $ z našeho příkladu a členu B ve vzorci odpovídá číslo 1 z našeho příkladu. Umocněním těchto členů dle vzorce druhé odmocniny ze jmenovatele zlomku zmizí a získáme celá čísla, protože $ (\sqrt{3})^2 = 3 $ a $ 1^2 = 1 $.

b)

\begin{align*} \frac{3}{\sqrt{5} + \sqrt{2}} &= \frac{3}{\sqrt{5} + \sqrt{2}} \cdot \frac{\sqrt{5} -\sqrt{2}}{\sqrt{5} -\sqrt{2}} = \frac{3(\sqrt{5} -\sqrt{2})}{5 -2} \\ &= \frac{3(\sqrt{5} -\sqrt{2})}{3} = \sqrt{5} -\sqrt{2} \end{align*}

Tento příklad jsme řešili obdobně jako předchozí, pouze jsme ve jmenovateli původního zlomku měli mezi jeho členy znaménko plus, takže jsme zlomek rozšířili výrazem se znaménkem minus, abychom mohli použít vzorec $ (A + B)(A -B) = A^2 + B^2 $. Členu A ve vzorci odpovídá číslo $ \sqrt{5} $ z příkladu a členu B ve vzorci odpovídá číslo $ \sqrt{2} $ z příkladu.

Usměrňování zlomků se provádí hlavně z toho důvodu, aby bylo možné rozeznat stejná čísla. Budeme-li mít např. čísla $ \frac{1}{\sqrt{2}} $ a $ \frac{\sqrt{2}}{2} $, nemusí být na první pohled jasné, zda jsou stejná nebo různá. Když u prvního zlomku, tedy $ \frac{1}{\sqrt{2}} $, provedeme jeho usměrnění, dostaneme druhý zlomek $ \frac{\sqrt{2}}{2} $ a víme tedy, že se jedná o stejná čísla.

Třetí odmocnina

Opět začneme definicí:

Třetí odmocnina z nezáporného reálného čísla a je takové nezáporné číslo x, pro které platí x³ = a. K jeho označení užíváme symbol $ \sqrt[3]{a} $.

Třetí odmocnina z nějakého čísla je tedy takové číslo, které když vynásobíme sebou samým tak, aby bylo v tomto součinu zastoupeno třikrát (čili ho umocníme na třetí), tak dostaneme právě to číslo, ze kterého třetí odmocninu počítáme.

Například:

$ \sqrt[3]{8} = 2 $, protože $ 2 \cdot 2 \cdot 2 = 2^3 = 8 $,

$ \sqrt[3]{64} = 4 $, protože $ 4 \cdot 4 \cdot 4 = 4^3 = 64 $,

$ \sqrt[3]{125} = 5 $, protože $ 5 \cdot 5 \cdot 5 = 5^3 = 125 $ atd.

Definice třetí odmocniny je v principu velmi podobná definici druhé odmocniny a obdobné jsou i věty pro počítání s třetími odmocninami.

Usměrnění zlomku s třetí odmocninou

Chceme-li provést usměrnění zlomku, který ve jmenovateli obsahuje třetí odmocninu, musíme zlomek rozšířit touto třetí odmocninou dvakrát, abychom ji v součinu měli celkem třikrát. Budeme-li chtít například z čísla $ \sqrt[3]{5} $ získat celé číslo 5, pak musíme číslo $ \sqrt[3]{5} $ vynásobit sebou samým dvakrát po sobě, tzn. že platí:

$$ \sqrt[3]{5} \cdot \sqrt[3]{5} \cdot \sqrt[3]{5} = 5 $$

Pokud ale násobíme dvakrát po sobě stejným číslem, pak vlastně násobíme tímto číslem umocněným na druhou. Takže místo $ \sqrt[3]{5} \cdot \sqrt[3]{5} $ můžeme napsat $ (\sqrt[3]{5})^2 $. Tento výraz můžeme dále upravit dle následujícího vzorce:

$$ (\sqrt[m]{a})^n = \sqrt[m]{a^n} $$

Tento vzorec říká, že když libovolnou odmocninu umocňujeme nějakým exponentem, můžeme si tento exponent napsat pod odmocninu přímo k danému číslu. Takže v našem příkladu platí:

$$ (\sqrt[3]{5})^2 = \sqrt[3]{5^2} $$

A podle tohoto pravidla budeme zlomky s třetí odmocninou ve jmenovateli rozšiřovat – místo dvojího násobení zlomek rozšíříme třetí odmocninou z čísla, které máme ve jmenovateli zlomku, umocněným na druhou. Ukážeme si to na příkladech:

Příklad 5

Usměrněte zlomky:

a) $ \frac{1}{\sqrt[3]{2}} $, b) $ \frac{2}{\sqrt[3]{3}} $, c) $ \frac{2}{\sqrt[3]{9}} $.

Řešení

a)

\[ \frac{1}{\sqrt[3]{2}} = \frac{1}{\sqrt[3]{2}} \cdot \frac{\sqrt[3]{2^2}}{\sqrt[3]{2^2}} = \frac{\sqrt[3]{4}}{\sqrt[3]{2^3}} = \frac{\sqrt[3]{4}}{2} \]

b)

\[ \frac{2}{\sqrt[3]{3}} = \frac{2}{\sqrt[3]{3}} \cdot \frac{\sqrt[3]{3^2}}{\sqrt[3]{3^2}} = \frac{2 \sqrt[3]{9}}{\sqrt[3]{3^3}} = \frac{2 \sqrt[3]{9}}{3} \]

c)

\[ \frac{2}{\sqrt[3]{9}} = \frac{2}{\sqrt[3]{3^2}} \cdot \frac{\sqrt[3]{3}}{\sqrt[3]{3}} = \frac{2 \sqrt[3]{3}}{\sqrt[3]{3^3}} = \frac{2 \sqrt[3]{3}}{3} \]

V posledním příkladu jsme postupovali trochu jinak – číslo 9 pod třetí odmocninou ve jmenovateli původního zlomku jsme si vyjádřili jako $ 3^3 $ a pak už stačilo zlomek rozšířit pouze číslem $ \sqrt[3]{3} $.

Závěr

V tomto článku jsme se zabývali druhou a třetí odmocninou reálných čísel a s tím souvisejícím usměrňováním zlomků.

V následujícím článku se budeme věnovat absolutní hodnotě.