Co jsou a jak se řeší rovnice

Vítejte u série věnované lineárním rovnicím a nerovnicím s jednou neznámou a jejich soustavám. V tomto článku si vysvětlíme úplné základy toho, jak rovnice fungují a jak se řeší.

Lineární rovnicí se myslí takové ty „obyčejné“ rovnice, se kterými se v matematice setkáte nejčastěji. Tzn. rovnice, které neobsahují nic „speciálního“, jako např. neznámou pod odmocninou, logaritmy, goniometrické funkce apod. Ani v nich nemáme neznámou umocněnou například na druhou – v tomto případě by se jednalo o kvadratickou rovnici.

Rovnice je zápis rovnosti dvou výrazů, v nichž se může vyskytovat nějaké písmeno (x, y, t apod.), které označuje tzv. neznámou. Například:

$$ 4 + x = 2 + 2x $$

Vyřešit rovnici znamená najít takové číslo, jehož dosazením do rovnice za neznámou dostaneme platnou rovnost.

Můžeme zkusit dosadit do naší rovnice za x např. číslo 4:

\begin{align*}
4 + 4 = 2 + 2 \cdot 4 \\
8 = 2 + 8 \\
8 \neq 10
\end{align*}

Dostali jsme neplatnou rovnost, takže číslo 4 není řešením rovnice. Mohli bychom zkoušet jiná čísla, jenže jaká? Čísel je nekonečně mnoho, takže takovýto způsob hledání řešení rovnice by mohl trvat hodně dlouho. A to je naše rovnice ještě velmi jednoduchá, takže bychom to možná uhodli správně, ale u složitějších rovnic bychom mohli hádat prakticky do nekonečna. Asi uznáte, že tohle zkrátka není dobrá cesta.

Ekvivalentní úpravy

Naštěstí existují jiné způsoby. Nejpoužívanějším z nich je postup, kdy provádíme s rovnicí tzv. ekvivalentní úpravy tak, abychom se dopracovali k rovnici, kdy na jedné straně budeme mít pouze neznámou a na druhé straně číslo, jehož hodnota této neznámé odpovídá. Toto výsledné číslo se nazývá řešení rovnice, nebo také kořen rovnice.

Pokud provedeme s rovnicí ekvivalentní úpravu, dostaneme sice jinou (změněnou) rovnici, která ale bude mít stále stejné řešení.

Zjednodušeně řečeno to znamená, že si kdykoli můžeme k oběma stranám rovnice něco přičíst, něco od nich odečíst, něčím je vynásobit nebo něčím je vydělit. A samozřejmě si můžeme prohodit levou stranu s pravou.

Musíme to ale udělat opravdu s oběma stranami – když si například od pravé strany odečteme číslo 4, musíme toto číslo odečíst také od strany levé.

Rovnice jako miskové váhy

Pro větší názornost si můžeme rovnici představit jako miskové váhy, viz následující obrázek:

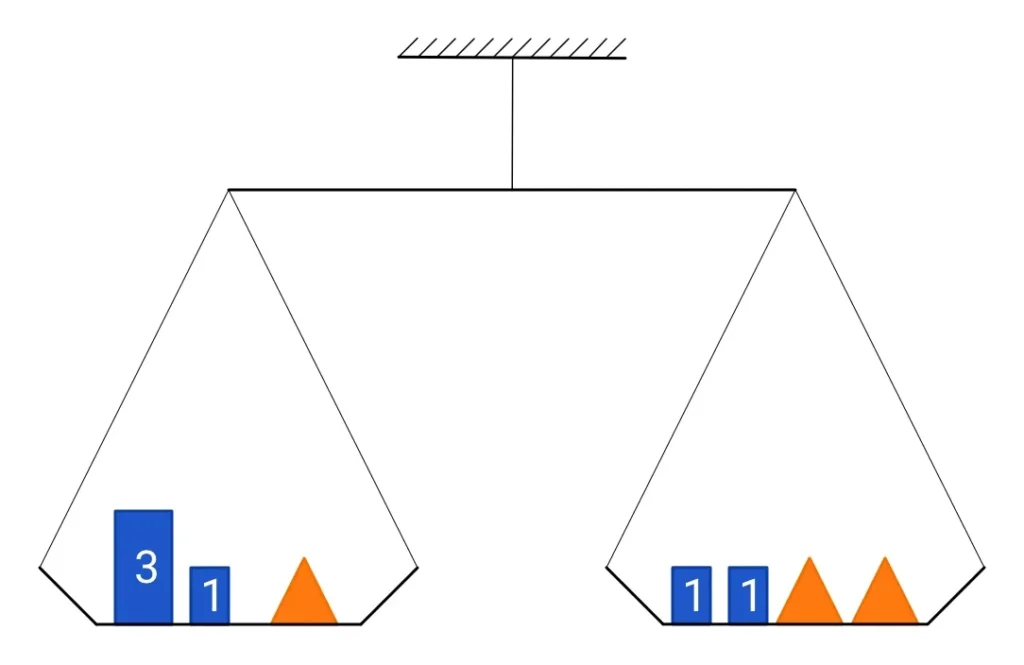
Na levé misce máme dvě závaží – dejme tomu, že čísla reprezentují hmotnost těchto závaží v gramech, takže celková hmotnost obou závaží na levé misce je 4 gramy. Dále je zde jeden oranžový trojúhelník, který reprezentuje neznámou x – můžete si představit, že je to třeba kousek zlata. 🙂 Když si obsah této levé misky přepíšeme do matematického výrazu, bude vypadat takto:

$$ 4 + x $$

Na pravé misce máme rovněž dvě závaží o celkové hmotnosti 2 gramy a dva oranžové trojúhelníky, tedy celkem dvě neznámé x. Odpovídající matematický výraz bude vypadat takto:

$$ 2 + 2x $$

Protože jsou misky v rovnováze, tzn. že hmotnost levé misky se rovná hmotnosti pravé misky, můžeme mezi tyto výrazy napsat „rovná se“, čímž vytvoříme rovnici:

$$ 4 + x = 2 + 2x $$

Nyní můžeme na obě misky něco přidávat nebo z nich něco odebírat, ale tak, aby stále zůstávaly v rovnováze, přičemž naším cílem bude zjistit, kolik váží oranžový trojúhelník reprezentující naši neznámou x.

Jako první můžeme z každé misky odebrat jeden oranžový trojúhelník, čímž provedeme ekvivalentní úpravu odečtení stejného čísla nebo výrazu od obou stran rovnice. Pokud se chystáme provést ekvivalentní úpravu, můžeme za rovnici napsat svislé lomítko a za něho právě tu úpravu, kterou se chystáme s rovnicí udělat – v našem případě odečíst neznámou x:

$$ 4 + x = 2 + 2x \qquad |-x $$

Po tomto odečtení nám na levé straně neznámá x zmizí, protože se odečte na nulu, a na pravé straně místo dvou x budeme mít jen jedno x. Rovnice po naší ekvivalentní úpravě bude vypadat takto:

$$ 4 = 2 + x $$

Odpovídající stav našich miskových vah po odebrání jednoho oranžového trojúhelníku by vypadal takto:

Nakonec odebereme z každé misky 2 gramy, čímž dosáhneme toho, že na pravé misce nám zbude pouze jeden oranžový trojúhelník, tedy jedno x, a na pravé straně místo 4 gramů budeme mít pouze 2 gramy.

Příslušný postup řešení naší rovnice bude vypadat následovně:

\begin{align*}
4 &= 2 + x \qquad |-2 \\
2 &= x
\end{align*}

Odpovídající proces na našich miskových vahách – tedy odebrání 2 gramů z každé misky, si můžeme představit tak, že jsme na levé misce nahradili obě závaží, která dohromady vážila 4 gramy, jen jedním, které váží 2 gramy, a na pravé misce jsme odebrali obě jednogramová závaží, která dohromady rovněž vážila 2 gramy:

Rovnice je vyřešená – její řešení neboli kořen je číslo 2. Pokud chceme, můžeme pro větší přehlednost prohodit levou stranu s pravou, abychom x měli vlevo a číslo vpravo:

$$ x = 2 $$

Proces řešení rovnice si tedy můžeme představit tak, jako bychom manipulovali s miskovými vahami. Pokud totiž na obě misky přidáme stejnou hmotnost nebo ji z obou misek odebereme, nebo pokud všechno, co na obou miskách máme, vynásobíme nebo vydělíme stejným číslem, tak stav misek se sice bude měnit, ale budou stále zůstávat v rovnováze.

V případě provádění ekvivalentních úprav během řešení rovnice to znamená, že rovnice se sice bude měnit, ale její strany se sobě budou stále rovnat.

Zkouška

Řešíme-li rovnici, provádíme někdy zkoušku. Můžeme mít k tomu dva důvody:

1. Rovnici jsme řešili s použitím tzv. důsledkových úprav. Důsledkovými úpravami se budeme zabývat u iracionálních rovnic.
2. Pokud jsme rovnici řešili pouze s pomocí ekvivalentních úprav, tak jak jsme je popsali v tomto článku, není zkouška nutná, a slouží pouze k ověření, že jsme rovnici počítali bez chyb. Nebo můžete mít ve škole zadáno, abyste zkoušku provedli.

Zkouška se dělá tak, že nejprve vezmeme výraz na levé straně původní rovnice, kterou jsme řešili, dosadíme do něho za neznámou číslo, které nám vyšlo, a spočítáme hodnotu tohoto výrazu. Potom provedeme stejný proces s výrazem, který tvoří pravou stranu původní rovnice.

Pokud nám vyjdou stejná čísla, pak je všechno v pořádku, ale pokud nám vyjdou různá čísla, pak jsme někde udělali chybu (pravděpodobně během výpočtu naší rovnice, ale není vyloučeno, že při provádění zkoušky).

Při provádění zkoušky musíme vyjít z té rovnice, kterou jsme dostali zadánu. Nemůžeme použít některou rovnici upravenou ekvivalentními úpravami, jež jsme postupně získávali během jejího řešení.

Proveďme zkoušku naší rovnice $ 4 + x = 2 + 2x $, kde nám vyšlo řešení (kořen) x = 2.

Nejdříve spočítáme hodnotu výrazu na levé straně rovnice, který označíme jako L. Někdy se ještě do závorky napíše, pro jaké číslo zkoušku provádíme, tzn. kořen rovnice. Napíšeme tedy $ L(2) = 4 + x $, následně za x dosadíme číslo 2 a spočítáme výsledek:

$$ L(2) = 4 + x = 4 + 2 = 6 $$

Dále spočítáme hodnotu výrazu na pravé straně rovnice, který označíme písmenem P, za které opět do závorky napíšeme kořen rovnice:

\begin{align*}
P(2) &= 2 + 2x = 2 + 2 \cdot 2 = \\
&= 2 + 4 = 6
\end{align*}

V obou případech nám vyšlo stejné číslo (6). To znamená, že hodnota výrazu na levé straně rovnice je stejná jako hodnota výrazu na pravé straně rovnice, což zapíšeme takto:

$$ L(2) = P(2) $$

Tím je zkouška provedená a víme, že jsme rovnici vyřešili správně.

Závěr

V tomto článku jsme si vysvětlili úplné základy toho, co jsou to rovnice, jak se řeší a jak se dělá zkouška.

V následujícím článku si spočítáme několik příkladů na jednoduché lineární rovnice.