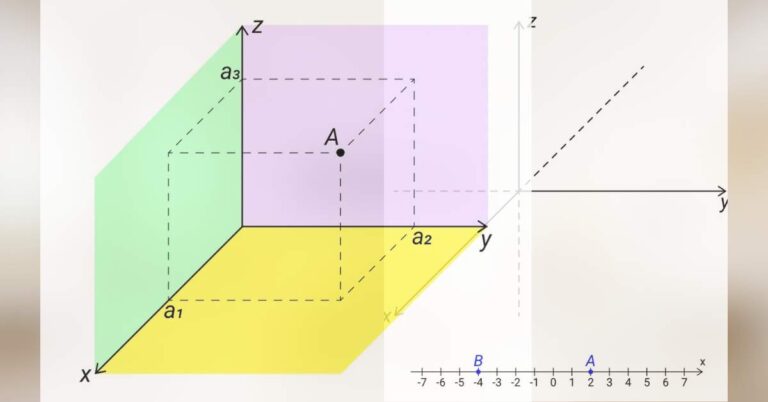
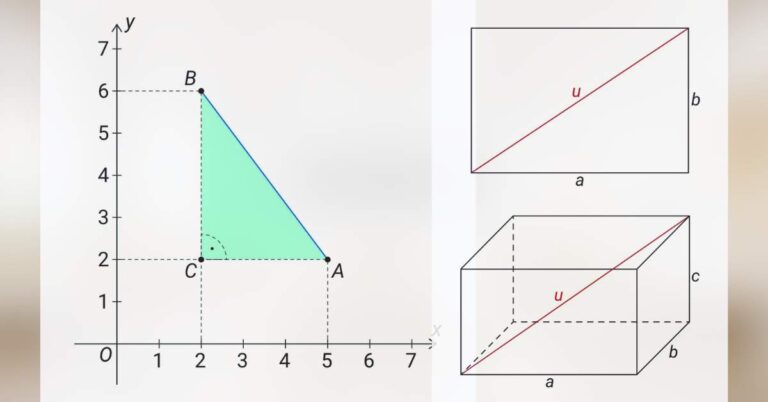
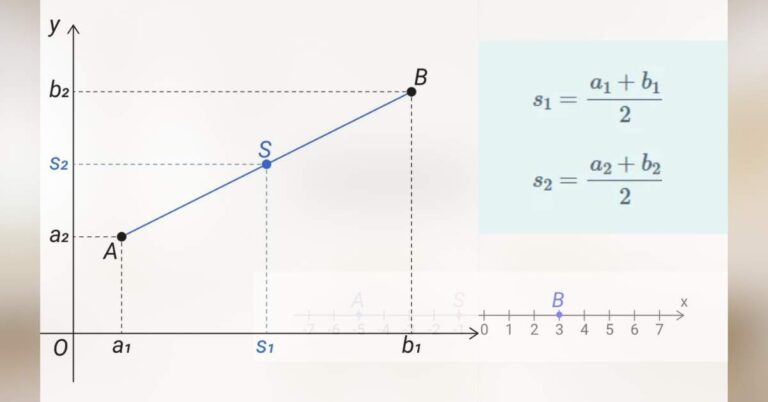
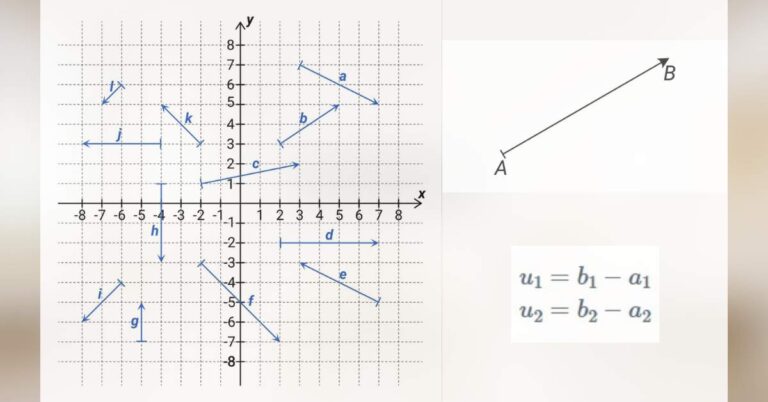
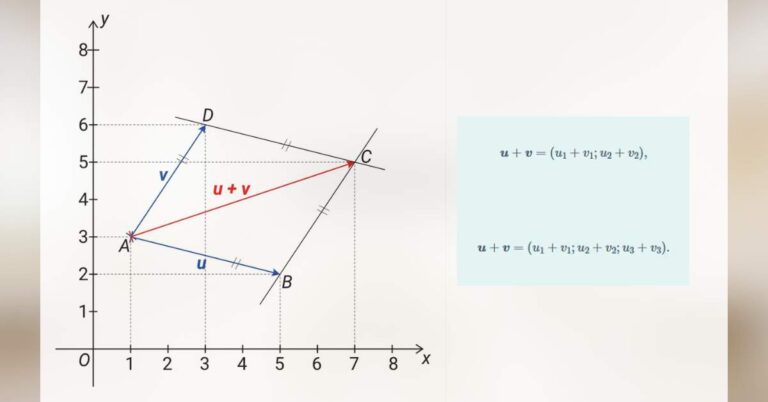
Souřadnice v rovině
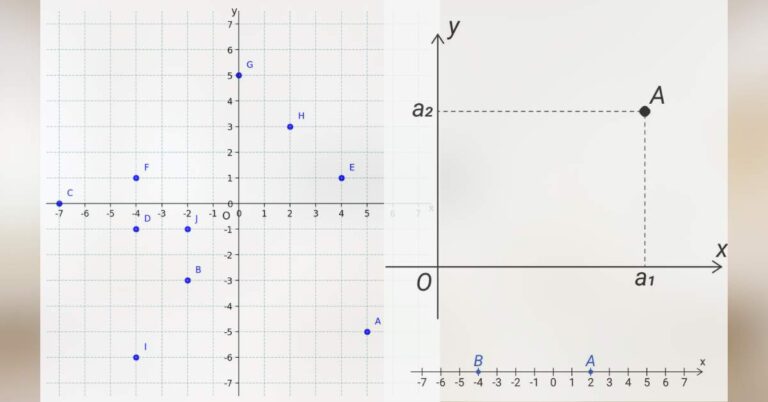
Vítejte u série věnované úvodu do analytické geometrie. Analytická geometrie je zjednodušeně řečeno „geometrie převedená na čísla“. Různé vlastnosti geometrických útvarů v rovině nebo v prostoru zde neurčujeme tím, že bychom tyto útvary precizně rýsovali a pak příslušné hodnoty odměřovali,…