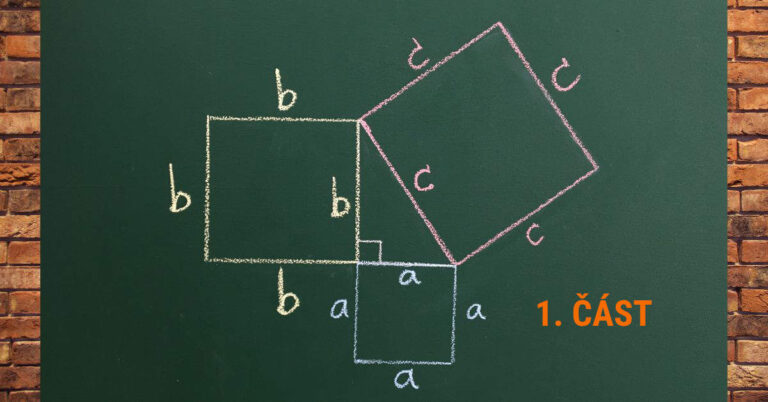
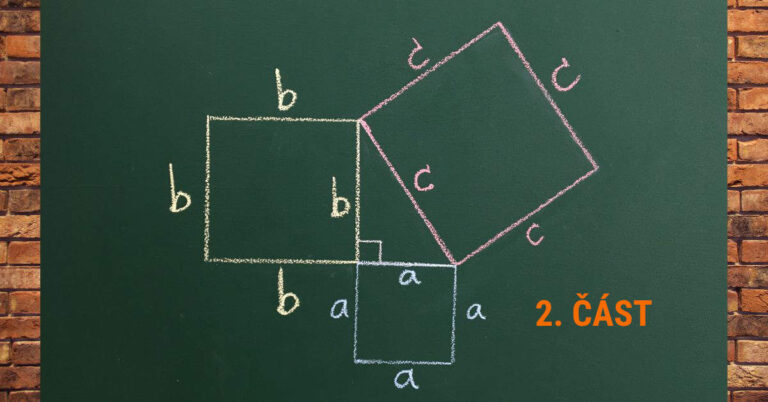
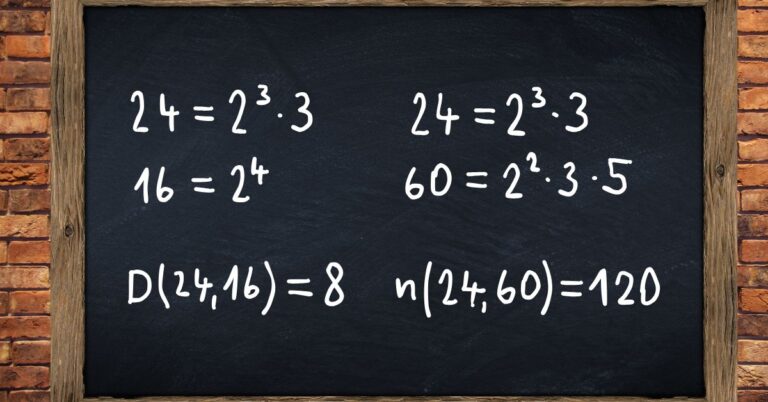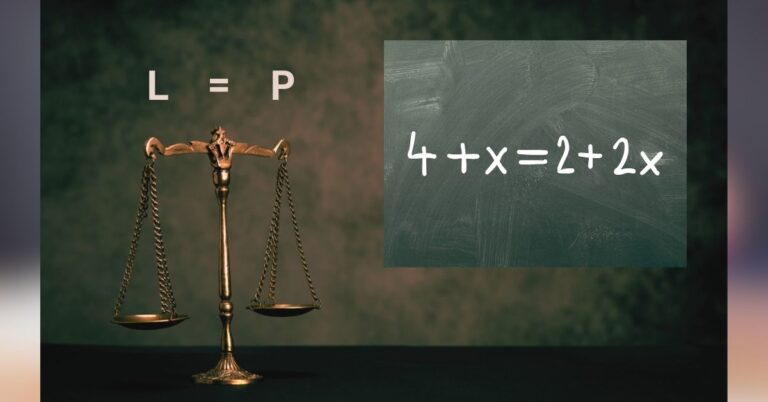Číselné obory – 1. část

Čísla jsou hlavním stavebním kamenem celé matematiky. Sice existují matematické struktury a oblasti, ve kterých se čísla nemusí vůbec vyskytovat (například značná část geometrie, teorie množin, výroková logika a další), ale pokud jde o matematiku, tak jak ji známe z běžného…