Kvadratické rovnice

Kvadratické rovnice jednoznačně patří mezi jedno z nejzákladnějších témat celé matematiky, které se opravdu vyplatí umět! Možná si říkáte, že jakmile je jednou ve škole proberete, budete mít od nich pokoj, ale pravý opak je pravdou.

Kvadratické rovnice jsou jako červená nit, jež se prolíná napříč většinou ostatních témat, která na to na první pohled nemusí vůbec vypadat. Zvláště často se s nimi setkáte při provádění různých substitucí u jiných druhů rovnic (například logaritmických či goniometrických), v analytické geometrii, u posloupností nebo při řešení různých slovních úloh. Dá se říci, že na vás mohou číhat prakticky všude.

Naštěstí se nejedná o nic složitého. Možná se vám článek bude zdát poněkud dlouhý a těm zkušenějším z vás budou následující věci jasné, ale protože stejně tak existuje početná skupina studentů, kteří v tomto tématu jasno nemají, rozhodl jsem se téma kvadratických rovnic rozebrat podrobněji. Pokud si článek přečtete až do konce, budete znát všechno nezbytné k tomu, abyste spočítali jakoukoli kvadratickou rovnici.

Pojďme si tedy krok za krokem a od úplných základů vysvětlit, co to kvadratická rovnice je, co je důležité o ní vědět, a především jak ji zdárně vyřešit.

Co je kvadratická rovnice

Zjednodušeně by se dalo říci, že kvadratická rovnice je taková rovnice, která někde obsahuje neznámou x ve druhé mocnině, tedy x². Samozřejmě to nemusí být vždycky pravda, protože mnohdy může rovnice v původním zadání nějaká ta x² obsahovat, ale během jejích úprav se vám stane, že je z obou stran rovnice bude možné odečíst, a tím pádem z ní zmizí.

Jindy zase můžete řešit rovnici, která v zadání žádné x² neobsahuje, ale pak si třeba někde roznásobíte závorky a najednou jej tam budete mít.

Proto se u složitěji zadaných rovnic nedá vždy hned poznat, jestli se o kvadratickou rovnici jedná nebo nejedná. Jednoznačně to vyplyne až v okamžiku, kdy vám v ní nějaký člen obsahující x² po všech předchozích úpravách zbude.

Uveďme si příklad: Dejme tomu, že budeme řešit rovnici, jejíž zadání bude poměrně složité, ale po různých úpravách se dopracujeme k následujícímu jednoduchému tvaru:

$$ 2x^{2} = 6 \; – \; x $$

V tomto okamžiku už je jasné, že se toho x² nijak nezbavíme a jde tedy o kvadratickou rovnici.

Ukážeme si tedy postup, jak ji vyřešit.

Anulovaný a základní tvar kvadratické rovnice

Jako první krok je potřeba si rovnici upravit do tzv. anulovaného tvaru. To znamená, že všechny členy si převedeme na levou stranu rovnice tak, aby nám vpravo zbylo číslo 0.

V našem příkladu neznámou x k rovnici přičteme (neboť je vpravo se záporným znaménkem) a číslo 6 naopak odečteme (je vpravo s kladným znaménkem, byť není před číslem napsané, protože znaménko plus se na začátku výrazů psát nemusí).

Po těchto úpravách dostaneme:

$$ 2x^{2} + x \; – \; 6 = 0 $$

Na tomto místě je dobré upozornit na to, že všechny členy na levé straně kvadratické rovnice je vhodné si seřadit od největších mocnin po nejmenší. To znamená, že na prvním místě zleva bude člen obsahující x², tedy x ve druhé mocnině, na druhém místě člen obsahující x bez exponentu (což je vlastně x v první mocnině) a jako poslední zde bude člen, který neobsahuje už vůbec žádné x, tedy jen holé číslo.

Tvar rovnice, který nyní máme, je nejen anulovaný, ale také základní – to znamená, že všude máme krásná celá čísla, a ne například zlomky.

Následující rovnice je také anulovaná:

$$ x^{2} + \frac{1}{2}x \; – \; \frac{2}{3} = 0 $$

Ale máme v ní zlomky. Pokud ji celou vynásobíme společným jmenovatelem těchto zlomků, tedy číslem 6, dostaneme:

$$ 6x^{2} + 3x \; – \; 4 = 0 $$

Touto úpravou jsme se zlomků z rovnice zbavili a máme v ní opět celá čísla. Postup, který je uveden dále, by sice fungoval i se zlomky, ale s celými čísly se nám bude lépe a snadněji počítat. Proto je výhodné mít rovnici v základním tvaru vždy, pokud je to možné.

Členy a koeficienty kvadratické rovnice

Vraťme se ale k naší původní rovnici:

$$ 2x^{2} + x \; – \; 6 = 0 $$

kterou máme v základním a anulovaném tvaru. Teď přijde jeden zásadní okamžik: Od této chvíle budeme všechno další počítat pouze pomocí takzvaných koeficientů. (Někdy se dají použít určité zkratky, kdy to jde i trochu jinak – o těch si povíme v příštích dílech tohoto miniseriálu.)

Ještě předtím, než si blíže vysvětlíme vlastní koeficienty, nebude na škodu zmínit, jak se nazývají jednotlivé členy kvadratické rovnice. Členy jsou výrazy, které jsou od sebe odděleny znaménky plus nebo mínus.

Vidíme, že kvadratická rovnice má na levé straně členy tři, které se po řadě nazývají takto:

• Kvadratický člen – to je vždy ten, který obsahuje neznámou x ve druhé mocnině, tedy x² (v našem případě je to výraz 2x²).
• Lineární člen – to vždy ten, který obsahuje neznámou x v první mocnině, tedy x bez exponentu (v našem případě +x).
• Absolutní člen – to je vždy ten, který neobsahuje neznámou vůbec, ale jen holé číslo (v našem případě -6).

Jestliže rovnice obsahuje všechny tři členy, nazývá se úplná kvadratická rovnice. Pokud některý člen chybí, pak jde o neúplnou kvadratickou rovnici. I neúplnou kvadratickou rovnici lze vyřešit postupem popsaným níže – pouze si do příslušného vzorce dosadíte za chybějící koeficient (viz příští odstavec) nulu. Ale protože u neúplných kvadratických rovnic existují určité zkratky umožňující vyřešit je snadněji a rychleji, pojednáme o nich v příštím díle této minisérie.

Koeficienty kvadratické rovnice jsou pak čísla, která značíme písmeny a, b, c. Uveďme si jejich význam a způsob, jak je správně z rovnice identifikovat:

• Koeficient a se vztahuje ke kvadratickému členu. Je to číslo, které násobí x² (v našem případě tedy číslo 2. Kdyby před x² nebylo žádné číslo, byl by koeficient a roven jedné).*
• Koeficient b se vztahuje k lineárnímu členu a je to číslo, které násobí x bez exponentu (v našem případě tedy číslo 1 – sice tam není napsáno, ale to x je tam jen jedno – klidně bychom si mohli tu jedničku před x dopsat).
• Koeficient c je samotný absolutní člen, tedy samotné číslo bez neznámé x (v našem případě ‑6).

Pro všechny koeficienty platí, že se k nim vztahuje i znaménko před nimi! Před výrazem 2x² je „neviditelné“ znaménko plus, před samotným x je také plus a před číslem 6 je znaménko mínus. Kdybychom v rovnici měli místo +x například –x, byl by koeficient b roven číslu -1.

* Poznámka: Pro koeficient a platí podmínka, že se nesmí rovnat nule. Nedošlo by sice k žádné zakázané operaci, ale kdybychom měli v rovnici 0x², tak celý tento člen by byl rovněž roven nule a z rovnice by úplně zmizel. A to, co by nám zůstalo, už by nebyla rovnice kvadratická, ale lineární.

Obecný tvar kvadratické rovnice

V učebnicích se u různých druhů rovnic obvykle jako první věc uvádí jejich tzv. obecný tvar. To je matematický předpis, kterému musí daná rovnice odpovídat, abychom o ní mohli jednoznačně říci, že se jedná právě o daný druh rovnice, a ne o žádný jiný.

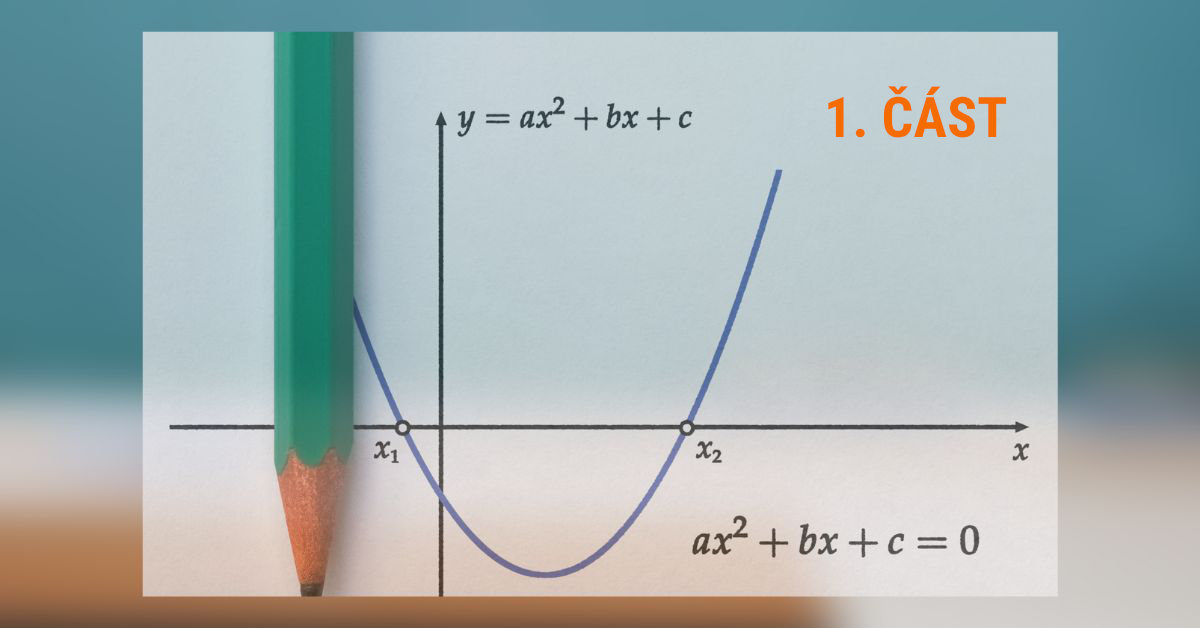
Obecný tvar kvadratické rovnice vypadá následovně:

$$ ax^{2} + bx + c = 0 $$

kde x je naše neznámá a písmena a, b, c jsou výše popsané koeficienty.

Jak jsme již uvedli, koeficienty mohou být samozřejmě i záporné a tím pádem se z některého znaménka plus může stát mínus. Možná se tedy ptáte, proč jsou v obecném tvaru přítomná pouze znaménka plus. Ale to nepředstavuje problém – naši rovnici, kterou v tomto článku řešíme, bychom klidně mohli zapsat i takto:

$$ 2x^{2} + 1x + (-6) = 0  $$

Jak můžete vidět, tento tvar odpovídá tvaru obecnému, ve kterém jsou mezi jednotlivými členy všude znaménka plus, a tím pádem můžeme naši rovnici právem nazvat kvadratickou.

Kromě obecného tvaru kvadratické rovnice existují i tvary jiné, například tvar normovaný, o kterém se zmíníme v některém z dalších článků na toto téma.

Diskriminant

Vraťme se k naší rovnici:

$$ 2x^{2} + x \; – \; 6 = 0 $$

a vypišme si její koeficienty:

a = 2
b = 1
c = -6

Prvním krokem řešení kvadratické rovnice v základním tvaruje výpočet tzv. diskriminantu. Diskriminant je číslo, které značíme velkým písmenem D a vypočítáme ho pomocí prvního klíčového vzorce, který opravdu doporučuji si dobře zapamatovat:

$$ D = b^{2} \; – \; 4ac $$

Vypočtením diskriminantu zjistíme, kolik řešení kvadratická rovnice má. Mohou nastat tyto případy:

• Jestliže diskriminant bude kladný (D > 0), pak má kvadratická rovnice dvě řešení (nebo také říkáme dva kořeny).
• Jestliže diskriminant bude roven nule (D = 0), pak má kvadratická rovnice jedno řešení (jeden tzv. dvojnásobný kořen).
• Jestliže diskriminant bude záporný (D < 0), pak kvadratická rovnice nemá žádné řešení (žádný kořen).**

** Poznámka: Přesněji, pokud je diskriminant záporný, rovnice nemá řešení v oboru reálných čísel, ale má řešení v oboru čísel komplexních, což je ovšem již trochu jiná oblast matematiky, která přesahuje rámec tohoto článku.

Vypočítáme diskriminant naší rovnice:

\[
\begin{align*}
D &= b^{2} \; – \; 4ac = 1^{2} \; – \; 4 \cdot 2 \cdot (-6) = \\
&= 1 \; – \; (-48) = 1 + 48 = 49
\end{align*}
\]

Všimněte si, že díky tomu, že koeficient c je v našem případě záporný, tak od výrazu b² odečítáme záporné číslo, takže nakonec onen násobek 4ac vlastně přičítáme – záměrně na to upozorňuji, protože právě tady se často dělají chyby.

Diskriminant nám vyšel kladný, a proto má naše rovnice dvě řešení.

Kdyby diskriminant vyšel záporný, mohli bychom přestat počítat a prostě napsat, že rovnice nemá řešení. (Pokud bychom ji tedy zrovna neřešili v oboru komplexních čísel.)

Jestli vám diskriminant opravdu záporný vyjde, raději si jeho výpočet ještě jednou zkontrolujte, jestli jste se nespletli třeba ve znaménku. Příklady v písemkách nebo při zkoušení jsou většinou vymyšleny tak, aby diskriminant byl kladný nebo nulový, protože zkoušející chce zpravidla vědět, zda umíte u kvadratické rovnice dopočítat i její kořeny.

Samozřejmě to neplatí vždycky – některé příklady vás budou testovat právě z toho, zda víte, že v případě záporného diskriminantu rovnice řešení nemá, ale nebude jich tolik jako těch, které řešení mají.

Kořeny kvadratické rovnice

Pokud diskriminant není záporný, tak druhý a zároveň poslední krok, který musíme udělat, je vypočítat samotné kořeny kvadratické rovnice (neboli její řešení). To uděláme pomocí druhého klíčového vzorce, který rovněž doporučuji si opravdu dobře zapamatovat:

$$ x_{1,2} = \frac{-b \pm \sqrt{D}}{2a} $$

Tento vzorec může pro někoho vypadat poněkud záhadně, a tak ještě než se pustíme do konečného vyřešení našeho příkladu, něco málo si k němu řekneme.

Za prvé vidíme, že na levé straně je neznámá x označená dolními indexy 1 a 2. To je proto, že kvadratická rovnice s kladným diskriminantem má právě dva kořeny, a tak si je potřebujeme nějak rozlišit. Za druhé, v čitateli zlomku na pravé straně jsou znaménka plus a mínus napsané dohromady pod sebou. Opět se to týká toho, že rovnice má dva kořeny: Varianta vzorce se znaménkem plus se vztahuje k prvnímu kořenu a varianta s mínus k druhému.

Důvodem, proč se to píše takhle dohromady, je, že nemusíme počítat každý kořen úplně zvlášť, protože začátek výpočtu je pro oba kořeny stejný a zbytečně bychom psali některé věci dvakrát. Místo toho můžeme prostě začít počítat oba kořeny zároveň a výpočet rozvětvit až na konci.

Ukažme si to na naší rovnici:

$$ x_{1,2} = \frac{-b \pm \sqrt {D}}{2a} = \frac{-1 \pm \sqrt{49}}{2 \cdot 2} = \frac{-1 \pm 7}{4} $$

Až teď můžeme výpočet rozvětvit a dopočítat si oba kořeny samostatně:

$$ x_{1} = \frac{-1 + 7}{4} = \frac{6}{4} = \frac{3}{2} $$

$$ x_{2} = \frac{-1 \; – \; 7}{4} = \frac{-8}{4} = -2 $$

A máme hotovo. Příklad jsme úspěšně vyřešili. Pokud chcete, můžete si samozřejmě udělat zkoušku. Tu provedete pro každý kořen zvlášť a v obou případech se musí levá strana původní rovnice rovnat straně pravé.

Dva vzorce na konec, o kterých je dobré vědět, ale nemusíte si je nutně pamatovat

Možná se ptáte, jak při řešení postupovat, pokud vám diskriminant vyjde nulový. V takovém případě má rovnice jeden kořen, a vzorec pro jeho výpočet vypadá takto:

$$ x= \frac{-b}{2a} $$

Nemusíte se ho ale učit nazpaměť, protože přirozeně vyplyne ze vzorce pro výpočet kořenů, který jsme si již popsali. To znamená, že můžete začít počítat úplně stejně, jako kdyby byl diskriminant kladný. Ukažme si to na příkladu:

Dejme tomu, že při řešení nějaké kvadratické rovnice nám vyjde D = 0. Dosadíme si tedy do vzorce pro výpočet kořenů za diskriminant nulu:

\[
\begin{align*}
x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a} = \frac{-b \pm \sqrt{0}}{2a} = \\
&= \frac{-b \pm 0}{2a} = \frac{-b}{2a}
\end{align*}
\]

Druhá odmocnina z nuly je nula, kterou následně v čitateli přičítáme ke členu –b, resp. ji od něj odečítáme. Jenže pokud k něčemu přičítáme, resp. od něčeho odečítáme nulu, nestane se vůbec nic, takže nakonec nám ze vzorce zbude jen jednoduchý zlomek, ke kterému jsme se dopracovali, tedy:

$$ x= \frac{-b}{2a} $$

Na závěr bych rád zmínil ještě jeden vzorec, s nímž se u kvadratických rovnic můžete setkat, který umožňuje spočítat kořeny kvadratické rovnice rovnou, aniž bychom předtím počítali diskriminant zvlášť:

$$ x_{1,2} = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a} $$

Od vzorce pro výpočet kořenů, který jsme si popsali výše, se liší tím, že pod druhou odmocninou v čitateli zlomku zde místo D máme výraz b² – 4ac. Ale tento výraz je právě vzorec pro výpočet diskriminantu! Takže se vlastně jedná o složený vzorec, kdy jsme spojili samostatné vzorce pro výpočet diskriminantu a kořenů dohromady.

Já osobně doporučuji jej nepoužívat, ale vždy si nejdříve spočítat diskriminant a teprve potom kořeny, a to z těchto důvodů:

• Zpravidla je jednodušší si zapamatovat dva jednoduché vzorce než jeden složitý.
• Jak se spočítá samotný diskriminant, je užitečné vědět tak jako tak.
• Pokud vám diskriminant vyjde záporný, nemusíte počítat nic dalšího – můžete rovnou napsat, že rovnice nemá řešení.
• U složitějšího vzorce je vyšší pravděpodobnost, že někde ve výpočtu uděláte chybu.
• Pokud si spočítáte správně diskriminant a následně uděláte chybu při výpočtu kořenů, budete mít vyřešeno aspoň něco a možná za příklad v písemce dostanete nějaký ten bod.
• Budete mít nad řešeným příkladem lepší celkový přehled a neztratíte se tak snadno v tom, co právě děláte.

Ale pokud tento vzorec i přesto používat chcete a vašemu vyučujícímu nevadí, že si nebudete počítat diskriminant zvlášť, je to samozřejmě jen vaše věc. To, co jsem napsal, je jen doporučení – zvolte si takový způsob, který vyhovuje především vám.

Závěr

Probrali jsme všechnu nezbytnou teorii k vyřešení kvadratické rovnice a ukázali jsme si dané postupy na konkrétním příkladě. V našem případě šlo o úplnou kvadratickou rovnici.

Jakmile jsme měli rovnici v základním tvaru, všechno ostatní – diskriminant i kořeny – jsme spočítali čistě s pomocí koeficientů a, b, c, které jsme si z tohoto základního tvaru „extrahovali“.

V následujícím článku se podíváme na neúplné kvadratické rovnice. Řekneme si, čím se liší od rovnic úplných a jaké způsoby se dají použít pro jejich výpočet, které jsou o něco jednodušší a rychlejší než u kvadratických rovnic úplných.