Skalární součin vektorů

V předchozím článku jsme se zabývali násobením vektoru číslem a lineární kombinací vektorů.

V tomto článku se budeme věnovat další aritmetické operaci s vektory, kterou je skalární součin vektorů. Zatím jsme vektory sčítali, odčítali, nebo jsme vektor násobili číslem. Teď budeme násobit dva vektory navzájem.

Možná se ptáte, proč je před slovním spojením „součin vektorů“ slovo „skalární“. Je to jednak proto, že máme hned dva druhy násobení dvou vektorů. První z nich je právě skalární součin vektorů a druhým vektorový součin vektorů, kterému se budeme věnovat v následujícím článku.

Další důvod je ten, že skalární součin vektorů tvoří takovou „výjimku“, pokud jde o výsledek této operace. Když jsme sčítali nebo odčítali vektory, výsledkem byl vždy nějaký nový vektor. Výsledek násobení vektoru číslem je také vektor a jak uvidíme v dalším článku, výsledkem vektorového součinu vektorů bude rovněž vektor. Ale výsledkem skalárního součinu vektorů je číslo, tzn. nevznikne žádný nový vektor.

Skalární veličiny např. ve fyzice jsou takové veličiny, které mají pouze nějakou hodnotu, ale nemají směr (např. teplota, hmotnost, hustota atp.), protože skalár znamená v podstatě jen číselnou hodnotu bez určitého směru. A stejné je to se skalárním součinem vektorů – jako výsledek dostaneme skalár čili pouze číselnou hodnotu bez nějakého směru, který by z ní vytvořil vektor.

Velikost vektoru

Ještě než se pustíme do definice skalárního součinu vektorů, zavedeme pojem velikost vektoru:

Velikost vektoru u je velikost kterékoli orientované úsečky AB určující vektor u. Velikost vektoru u označujeme symbolem |u|. Jestliže |u| = 1, nazývá se vektor u jednotkový vektor.

Velikost vektoru je tedy délka šipky, která ho reprezentuje. Pokud máme vektor definovaný pomocí dvou bodů, např. jako u = B – A, pak velikost vektoru odpovídá vzdálenosti těchto bodů.

Rovné závorky se nejen v analytické geometrii obecně používají pro vyjádření délky úsečky, velikosti vektoru, vzdálenosti dvou bodů apod. Zkrátka všude kde určujeme nějakou délku nebo vzdálenost dvou objektů, což je v podstatě také délka.

Víme, že vzdálenost dvou bodů A[a₁; a₂], B[b₁; b₂] v rovině je rovna číslu

\[ |AB| = \sqrt{(b_1 -a_1)^2 + (b_2 -a_2)^2} \]

Obdobně vzdálenost dvou bodů A[a₁; a₂; a₃], B[b₁; b₂; b₃] v prostoru je rovna číslu

\[ |AB| = \sqrt{(b_1 -a_1)^2 + (b_2 -a_2)^2 + (b_3 -a_3)^2} \]

Dále víme, že souřadnice vektoru u = B – A v rovině jsou čísla $ u_1 = b_1 -a_1 $, $ u_2 = b_2 -a_2 $, resp. v prostoru ještě $ u_3 = b_3 -a_3 $. Když si tato čísla dosadíme za příslušné dvojčleny do vzorce pro vzdálenost bodů, tak zjistíme, že z toho vyplývá:

Vektor u je nulový právě tehdy, když jeho velikost je nulová, tj. když při jeho umístění splývá jeho počáteční bod s koncovým bodem.

Příklad 1

V prostoru je v dané kartézské soustavě souřadnic dán vektor u = (2; -6; 3). Určete jeho velikost.

Řešení

\begin{align*} |\boldsymbol{u}| &= \sqrt{u_1^2 + u_2^2 + u_3^2} = \sqrt{2^2 + (-6)^2 + 3^2} = \\ &= \sqrt{4 + 36 + 9} = \sqrt{49} = 7 \end{align*}

Skalární součin

Skalární součin vektorů je velmi důležitý. Jeho souvislost s velikostí vektoru si ukážeme za chvíli.

Skalární součin dvou vektorů tedy získáme tak, že spolu vynásobíme jejich x-ové souřadnice (s dolním indexem 1), y-ové souřadnice (s dolním indexem 2) a v prostoru ještě z-ové souřadnice (s dolním indexem 3), a tyto násobky sečteme.

Příklad 2

Vypočítejte skalární součin vektorů u = (1; 2; -1) a v = (3; 1; 5).

Řešení

\begin{align*} \boldsymbol{uv} &= u_1v_1 + u_2v_2 + u_3v_3 = \\ &= 1 \cdot 3 + 2 \cdot 1 + (-1) \cdot 5 = \\ &= 3 + 2 -5 = 0 \end{align*}

Vidíme, že na rozdíl od součinu dvou čísel se skalární součin dvou nenulových vektorů může rovnat nule.

Úhel vektorů

Souvislost skalárního součinu dvou vektorů a jejich velikostí je taková, že nám umožňuje spočítat úhel, který tyto dva vektory svírají.

Umístíme-li dva vektory do souřadného systému tak, aby jejich počátky ležely v jeho počátku – tedy v bodě O[0; 0], pak můžeme definovat úhel dvou vektorů takto:

Mají-li dva nenulové vektory u, v umístění OU, OV, nazývá se velikost konvexního úhlu UOV úhel vektorů u, v. Jsou-li přímky OU, OV navzájem kolmé, říkáme, že i vektory OU, OV jsou navzájem kolmé.

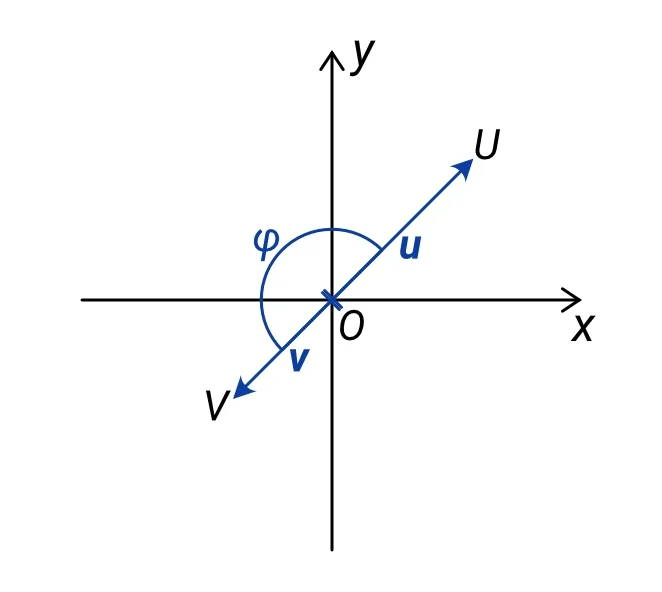
Následující obrázky znázorňují různé polohy vektorů u, v a jejich úhel.

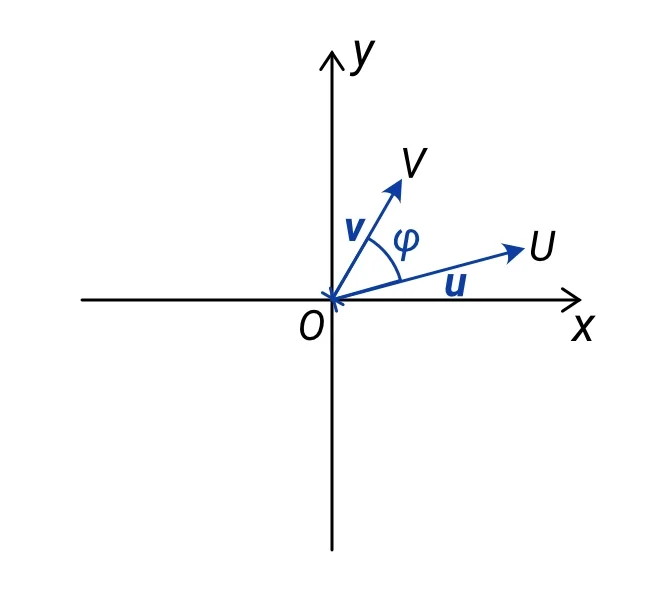
a) φ = 45°

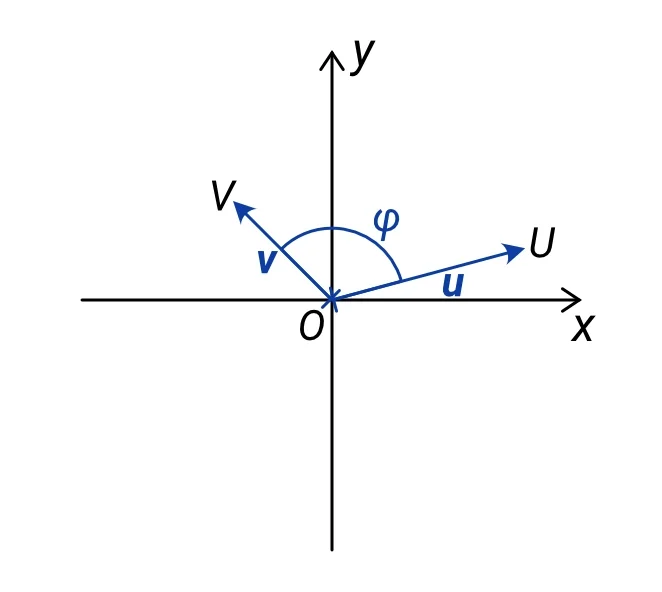
b) φ = 120°

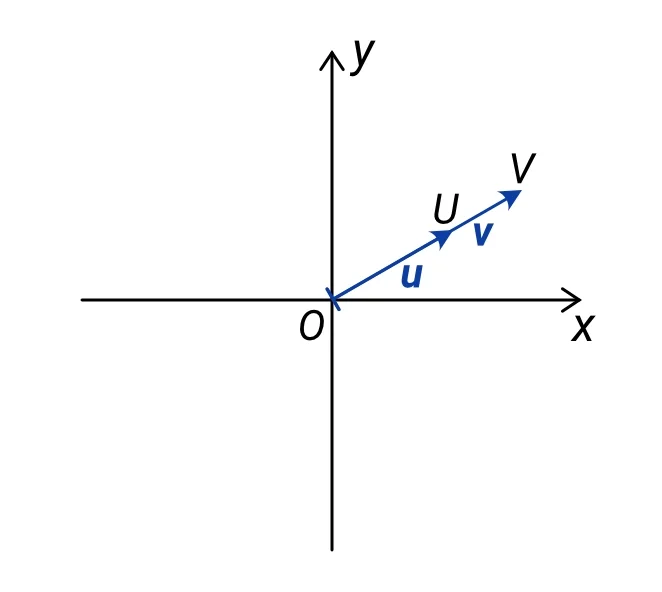
c) φ = 0

d) φ = 180°

Pokud by vektory byly v prostoru, doplnili bychom ještě osu z.

Teď půjdeme více do hloubky a odvodíme si vzorec pro úhel dvou vektorů. Pokud pro vás bude následující text příliš složitý, zapamatujte si alespoň ten vzorec, ke kterému dospějeme. 🙂

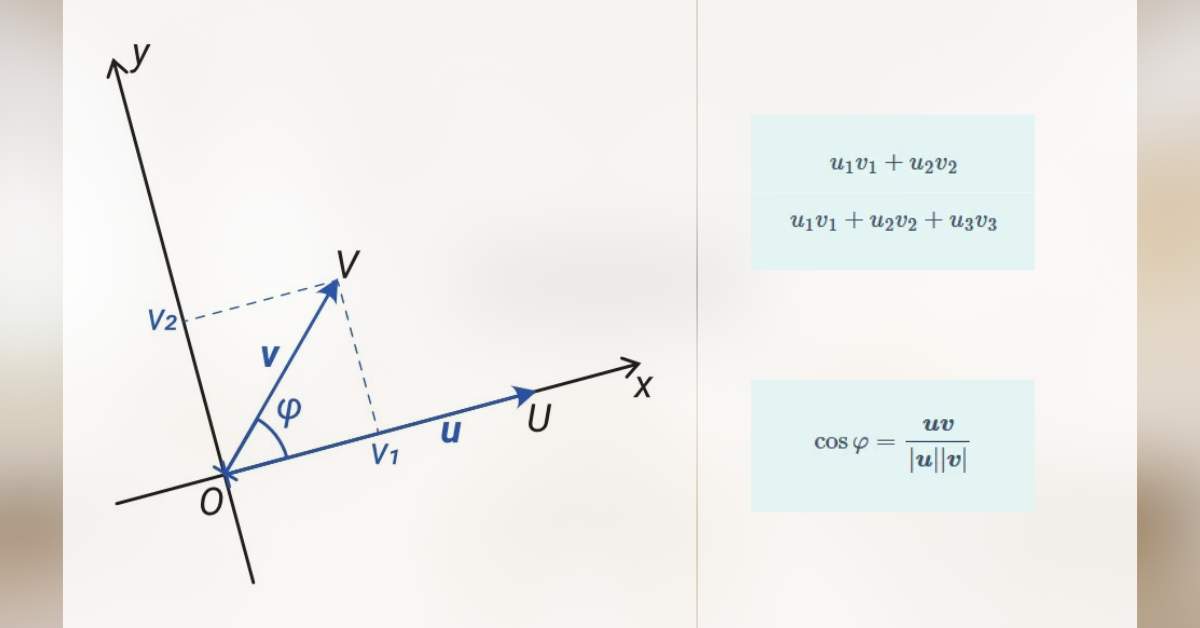
Otočme souřadný systém z prvního obrázku tak, aby vektor u ležel na ose x – viz následující obrázek:

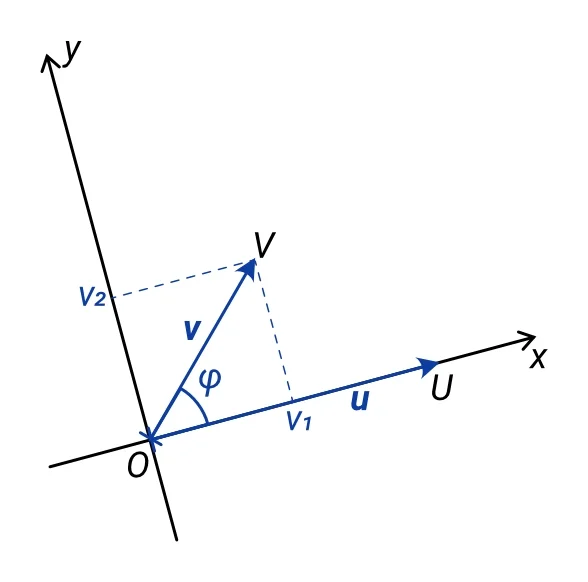
Potom x-ová souřadnice u₁ vektoru u bude určena jeho velikostí, zatímco jeho y-ová souřadnice u₂ bude nulová; x-ová souřadnice v₁ vektoru v bude mít hodnotu velikosti tohoto vektoru vynásobenou kosinem úhlu φ a jeho y-ová souřadnice v₂ bude mít hodnotu velikosti tohoto vektoru vynásobenou sinem úhlu φ. Matematicky tedy můžeme souřadnice obou vektorů vyjádřit takto:

$$ \boldsymbol{u} = (|\boldsymbol{u}|; 0) $$

$$ \boldsymbol{v} = (|\boldsymbol{v}| \cos \varphi; |\boldsymbol{v}| \sin \varphi) $$

Nyní pomocí těchto souřadnic vypočítáme skalární součin vektorů u, v:

\begin{align*} \boldsymbol{uv} &= u_1v_1 + u_2v_2 = \\ &= |\boldsymbol{u}||\boldsymbol{v}| \cos \varphi + 0 \cdot |\boldsymbol{v}| \sin \varphi = \\ &= |\boldsymbol{u}||\boldsymbol{v}| \cos \varphi \end{align*}

Dospěli jsme tedy ke vztahu:

$$ \boldsymbol{uv} = |\boldsymbol{u}||\boldsymbol{v}| \cos \varphi $$

Když tento vztah upravíme tak, že ho vydělíme výrazem |u||v|, dostaneme vzorec pro výpočet úhlu dvou vektorů:

$$ \cos \varphi = \frac{\boldsymbol{u}\boldsymbol{v}}{|\boldsymbol{u}||\boldsymbol{v}|} $$

Kosinus úhlu dvou vektorů tedy spočítáme tak, že jejich skalární součin vydělíme násobkem jejich velikostí.

Z tohoto vzorce vyplývá:

Skalární součin uv = 0 právě tehdy, je-li buď alespoň jeden z vektorů u, v nulový vektor, nebo jsou oba vektory nenulové a navzájem kolmé.

Tento poznatek budeme v analytické geometrii používat často. Protože skalární součin umožňuje rychle ověřit, zda jsou dva vektory kolmé, můžeme si pomocí něho rychle určit například vzájemnou polohu dvou přímek, přímky a roviny atd., jak uvidíme v dalších článcích.

Příklad 3

Vypočítejte úhel vektorů u, v.

a) u = (1; 1; -1), v = (2; 1; 3)

Řešení

Vypočítáme nejdříve skalární součin vektorů u, v:

\begin{align*} \boldsymbol{uv} &= u_1v_1 + u_2v_2 + u_3v_3 = \\ &= 1 \cdot 2 + 1 \cdot 1 + (-1) \cdot 3 = \\ &= 2 + 1 -3 = 0 \end{align*}

Protože skalární součin uv = 0, vektory jsou navzájem kolmé, tj. jejich úhel je 90°. (Nemusíme dále nic počítat.)

b) u = (0; 1; 2), v = (3; 3; -1)

Řešení

Vypočítáme nejdříve skalární součin vektorů u, v:

\begin{align*} \boldsymbol{uv} &= u_1v_1 + u_2v_2 + u_3v_3 = \\ &= 0 \cdot 3 + 1 \cdot 3 + 2 \cdot (-1) = \\ &= 0 + 3 -2 = 1 \end{align*}

Dále vypočítáme velikosti vektorů u, v:

\begin{align*} |\boldsymbol{u}| &= \sqrt{u_1^2 + u_2^2 + u_3^2} = \sqrt{0^2 + 1^2 + 2^2} = \\ &= \sqrt{0 + 1 + 4} = \sqrt{5} \end{align*}

\begin{align*} |\boldsymbol{v}| &= \sqrt{v_1^2 + v_2^2 + v_3^2} = \sqrt{3^2 + 3^2 + (-1)^2} = \\ &= \sqrt{9 + 9 + 1} = \sqrt{19} \end{align*}

Nyní vypočítané hodnoty dosadíme do vzorce pro výpočet úhlu vektorů:

\[ \cos \varphi = \frac{\boldsymbol{u}\boldsymbol{v}}{|\boldsymbol{u}||\boldsymbol{v}|} = \frac{1}{\sqrt{5} \sqrt{19}} = \frac{1}{\sqrt{95}} \]

Tuto hodnotu bychom zadali do kalkulačky jako argument funkce cos^-1, a dostali bychom výsledek:

$$ \varphi \doteq 84^\circ 6 ^{\prime} 41 ^{\prime} $$

Závěr

V tomto článku jsme se zabývali skalárním součinem vektorů a rozebrali jsme jeho souvislosti s úhlem vektorů, při jehož výpočtu zase potřebujeme umět spočítat velikost vektoru.

V následujícím článku se podíváme na vektorový a smíšený součin vektorů.