V předchozím článku jsme se zabývali vzdáleností bodů.
V tomto článku si vysvětlíme, jak můžeme určit střed úsečky, a ukážeme si příklady. Střed úsečky je charakterizován tím, že dělí úsečku na dvě stejné části.
Začneme číselnou osou. Máme-li na ní úsečku AB, potom jejímu středu odpovídá číslo
$$ s = \frac{a + b}{2} $$
kde a, b jsou souřadnice bodů A, B na číselné ose. Protože číselná osa je jednorozměrný útvar, stačí nám k určení souřadnice daného bodu jediné číslo.
Číslo s jsme určili jako aritmetický průměr čísel a, b. Aritmetický průměr spočítáme jako součet čísel děleno jejich počet – v našem případě děleno neboli lomeno dvěma. Je to logické, protože když počítáme aritmetický průměr pouze ze dvou čísel, vyjde nám hodnota, která je přesně mezi nimi, a střed úsečky leží přesně mezi jejími krajními body.
Budeme-li mít na číselné ose např. úsečku danou body A[-5] a B[3], pak souřadnice jejího středu – bodu S o souřadnici s – po dosazení do vzorce vyjde
$$ s = \frac{-5 + 3}{2} = \frac{-2}{2} = -1 $$
viz následující obrázek:

Střed úsečky v rovině
U úsečky v rovině budeme postupovat obdobně, ale protože zde body mají dvě souřadnice, vypočítáme aritmetický průměr pro každou z nich zvlášť. Podívejte se na následující obrázek:
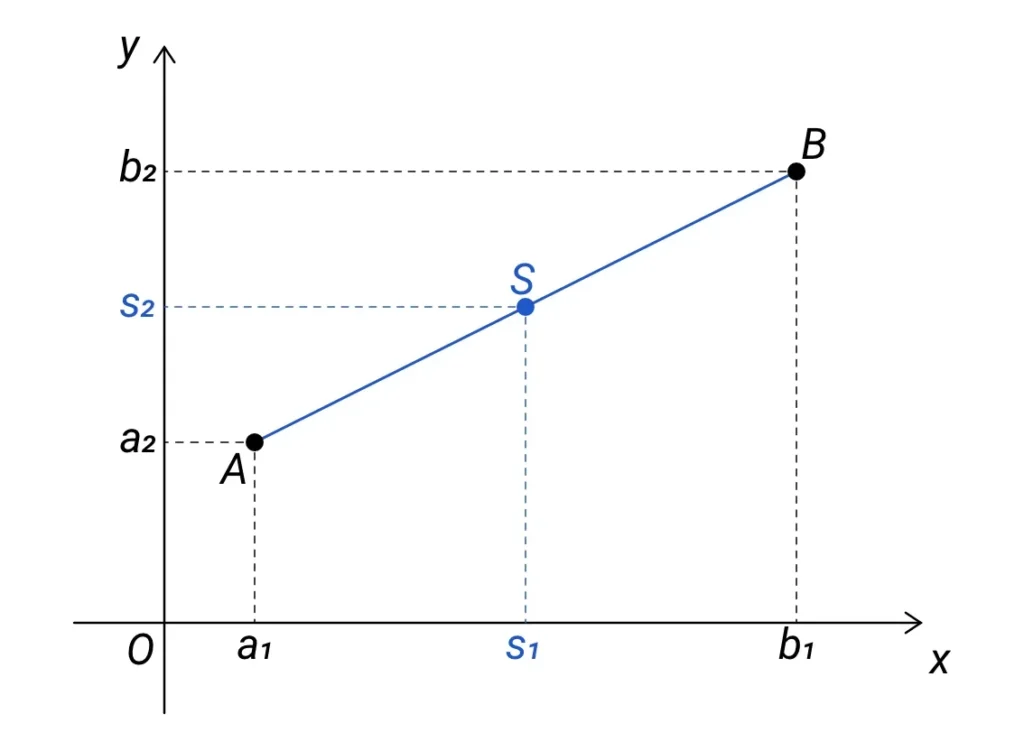
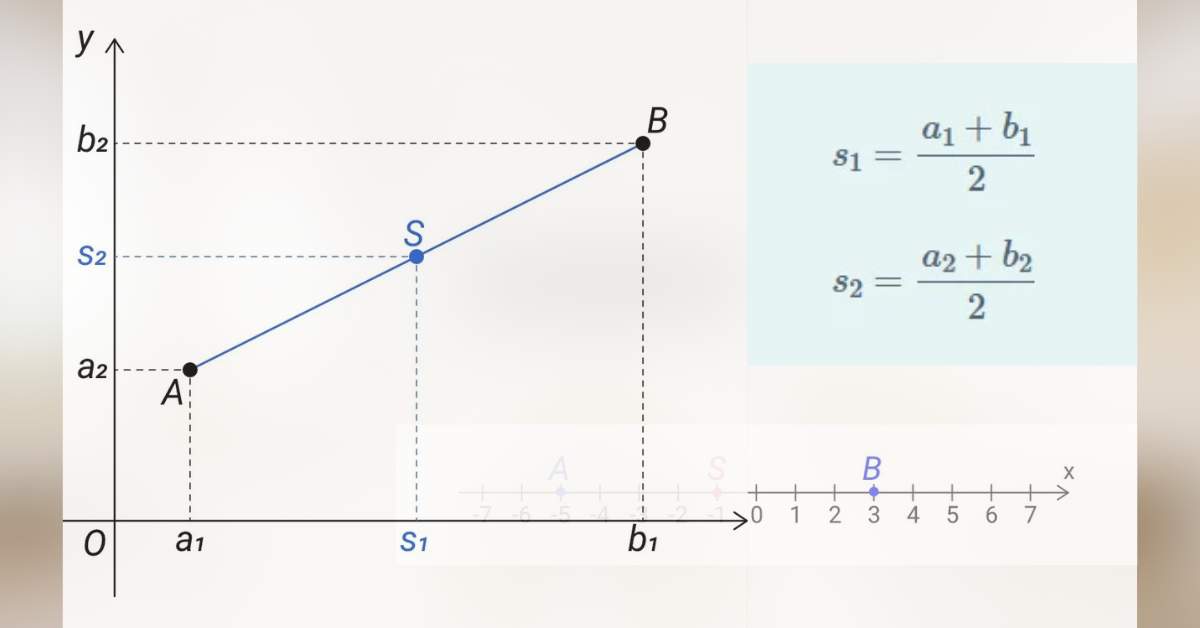
Bod S je střed úsečky AB. Jeho x-ová souřadnice s1 je přesně mezi x-ovými souřadnicemi bodů A, B, tedy mezi čísly a1 a b1. Obdobně jeho y-ová souřadnice s2 je přesně mezi y-ovými souřadnicemi bodů A, B, tedy mezi čísly a2 a b2. Číslo s1 je tedy aritmetickým průměrem čísel a1 a b1 a číslo s2 je aritmetickým průměrem čísel a2 a b2. Můžeme tedy vyslovit definici:
Pro střed S[s1; s2] úsečky AB, kde A[a1; a2], B[b1; b2], platí
$$ s_1 = \frac{a_1 + b_1}{2} $$
$$ s_2 = \frac{a_2 + b_2}{2} $$
Příklad 1
Jsou dány body A[–4; 3], B[6; 1]. Určete střed S úsečky AB.
Řešení
\[ s_1 = \frac{a_1 + b_1}{2} = \frac{-4 + 6}{2} = \frac{2}{2} = 1 \]
\[ s_2 = \frac{a_2 + b_2}{2} = \frac{3 + 1}{2} = \frac{4}{2} = 2 \]
$$ S[1; 2] $$
Střed úsečky v prostoru
V prostoru je situace opět analogická, pouze nám zde přibudou z-ové souřadnice krajních bodů úsečky a z-ová souřadnice jejího středu, což jsou souřadnice s dolním indexem 3. Můžeme tedy vyslovit podobnou definici jako u středu úsečky v rovině, do níž tuto třetí souřadnici doplníme:
Pro střed S[s1; s2; s3] úsečky AB, kde A[a1; a2; a3], B[b1; b2; b3], platí
$$ s_1 = \frac{a_1 + b_1}{2} $$
$$ s_2 = \frac{a_2 + b_2}{2} $$
$$ s_3 = \frac{a_3 + b_3}{2} $$
Příklad 2
Jsou dány body A[–7; 4; –3], B[–1; –4; 5]. Určete střed S úsečky AB.
\[ s_1 = \frac{a_1 + b_1}{2} = \frac{-7 +(-1)}{2} = \frac{-8}{2} = -4 \]
\[ s_2 = \frac{a_2 + b_2}{2} = \frac{4 +(-4)}{2} = \frac{0}{2} = 0 \]
\[ s_3 = \frac{a_3 + b_3}{2} = \frac{-3 + 5}{2} = \frac{2}{2} = 1 \]
$$ S [-4; 0; 1] $$
Příklad 3
Jsou dány body B[2; 0; 1], S[–1; –3; –2]. Určete bod A tak, aby bod S byl střed úsečky AB.
\begin{align*} s_1 &= \frac{a_1 + b_1}{2} \\ -1 &= \frac{a_1 + 2}{2} \qquad | \cdot 2 \\ -2 &= a_1 + 2 \qquad |-2 \\ a_1 &= -4 \end{align*}
\begin{align*} s_2 &= \frac{a_2 + b_2}{2} \\ -3 &= \frac{a_2 + 0}{2} \qquad | \cdot 2 \\ a_2 &= -6 \end{align*}
\begin{align*} s_3 &= \frac{a_3 + b_3}{2} \\ -2 &= \frac{a_3 + 1}{2} \qquad | \cdot 2 \\ -4 &= a_3 + 1 \qquad |-1 \\ a_3 &= -5 \end{align*}
$$ A[-4; -6; -5] $$
Závěr
V tomto článku jsme si ukázali, jak se vypočítají souřadnice středu úsečky, a zakončili jsme tak sérii věnovanou souřadnicím.
V následujícím článku se začneme věnovat dalším velice důležitým elementům, na kterých je analytická geometrie v podstatě postavená, a sice vektorům.