Souřadnice v rovině

Vítejte u série věnované úvodu do analytické geometrie. Analytická geometrie je zjednodušeně řečeno „geometrie převedená na čísla“. Různé vlastnosti geometrických útvarů v rovině nebo v prostoru zde neurčujeme tím, že bychom tyto útvary precizně rýsovali a pak příslušné hodnoty odměřovali, ale určujeme je jednoznačnými výpočty.

Abychom však mohli tyto výpočty provádět, potřebujeme tyto útvary a jejich polohy v rovině či v prostoru matematicky popsat. Naprostým základem k takovému popisu jsou souřadnice v rovině a souřadnice v prostoru. V tomto článku se podíváme na souřadnice v rovině.

Jeden rozměr – číselná osa

Asi umíte vyznačit obraz čísla na číselnou osu. Číselná osa je přímka, na které si zvolíme počátek – číslo 0, a jednotku – např. 1 centimetr. Tento počátek, tedy číslo 0, nám rozdělí číselnou osu na dvě polopřímky, podle kterých si zvolíme orientaci této osy – zpravidla obrazy všech kladných čísel kreslíme od čísla 0 směrem doprava a obrazy záporných čísel směrem doleva. Kladný směr této osy značíme šipkou. Viz následující obrázek:

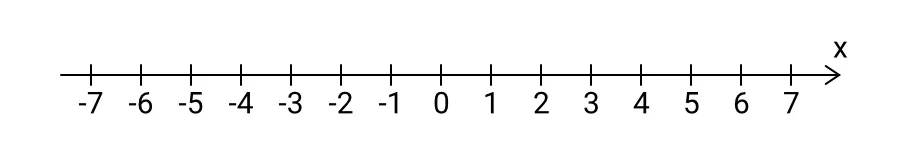
Přímka je jednorozměrný útvar, proto k vyznačení polohy bodu na ní nám stačí pouze jedno číslo. Například na následujícím obrázku jsou vyznačeny dva body: A = 2 a B = -4:

My žijeme v třírozměrném prostoru, ale většinou se vyskytujeme na povrchu Země, který je dvourozměrný. Jde vlastně o zakřivenou plochu, ale toto zakřivení můžeme pro relativně malé vzdálenosti zanedbat. V praktickém životě jsme zvyklí nějakým způsobem udávat polohu – například obchodu, našeho bydliště, místa schůzky apod. Děláme to zpravidla tak, že udáme ulici a číslo domu, případně město a stát. Ale co třeba na moři, kde nejsou žádná města ani ulice? Tam udáváme polohu dvěma čísly – zeměpisnou délkou a zeměpisnou šířkou.

V rovině už nám k určení polohy zkrátka nestačí jen jedno číslo, např. na zmíněném moři potřebujeme vědět, jak daleko na východ, resp. na západ, jsme vzdáleni od nultého poledníku (zeměpisná délka), a jak daleko na sever, resp. na jih, jsme vzdáleni od rovníku (zeměpisná šířka).

Dva rozměry – soustava souřadnic v rovině

Podobně budeme postupovat také my – body v rovině určíme dvěma čísly. K tomu si vytvoříme tzv. soustavu souřadnic, která bude mít číselné osy dvě, jež označíme jako x a y. Speciálně půjde o kartézskou soustavu souřadnic v rovině, pro kterou platí následující definice:

Budeme-li kreslit kartézskou soustavu souřadnic, budeme písmeno označující danou číselnou osu připisovat vždy k příslušné kladné poloose – viz následující obrázek:

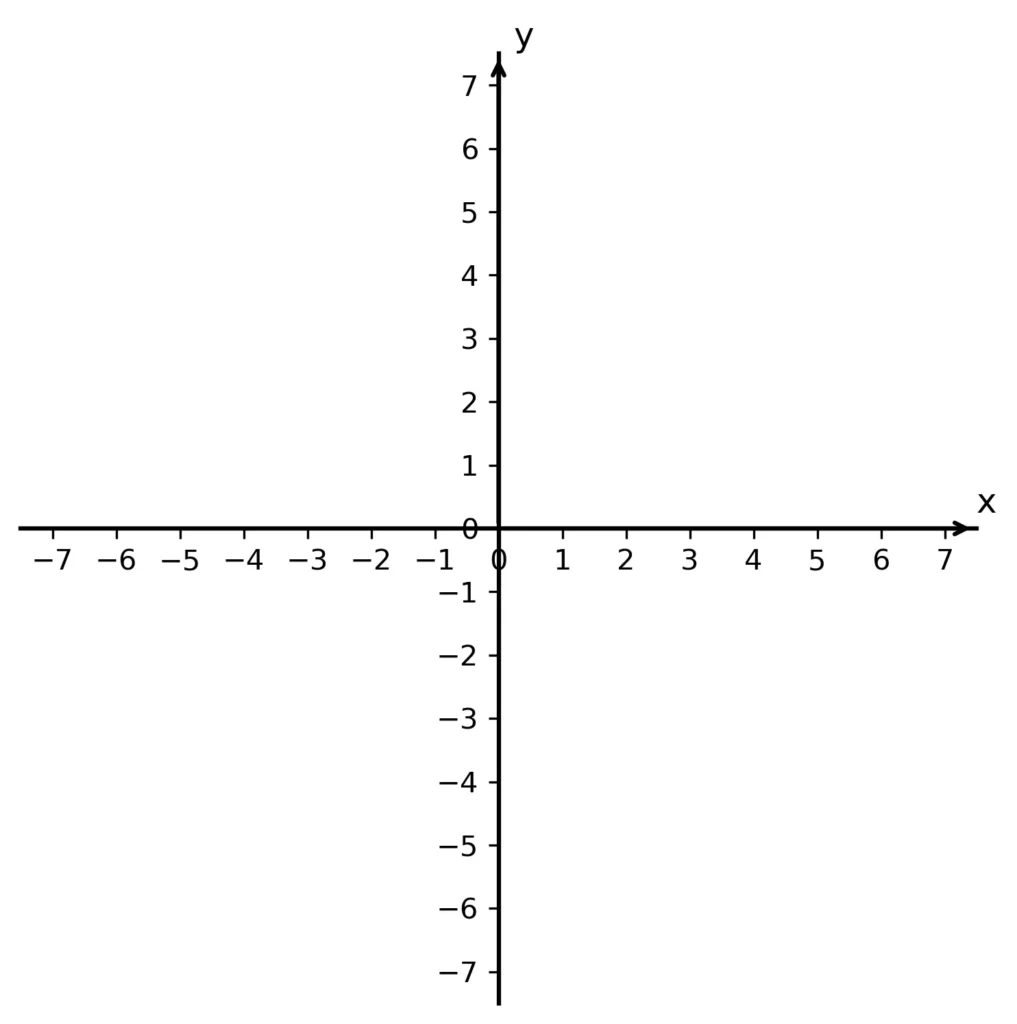
Polohu bodu v této soustavě souřadnic určíme pomocí dvou čísel takto:

• První z těchto čísel představuje x-ovou souřadnici bodu a udává, jak daleko je tento bod od osy y směrem doprava nebo doleva, přičemž směr doprava je kladný a směr doleva záporný.
• Druhé z těchto čísel představuje y-ovou souřadnici bodu a udává, jak daleko je tento bod od osy x směrem nahoru nebo dolů, přičemž směr nahoru je kladný a směr dolů záporný.

Tato čísla se nazývají souřadnice daného bodu a zapisujeme je jako uspořádané dvojice do hranatých závorek hned za označení daného bodu. (Mezi označení bodu a jeho souřadnice se nepíše znak „rovná se“.) Ukažme si příklad.

Příklad 1

Zobrazte v kartézské soustavě souřadnic následující body:

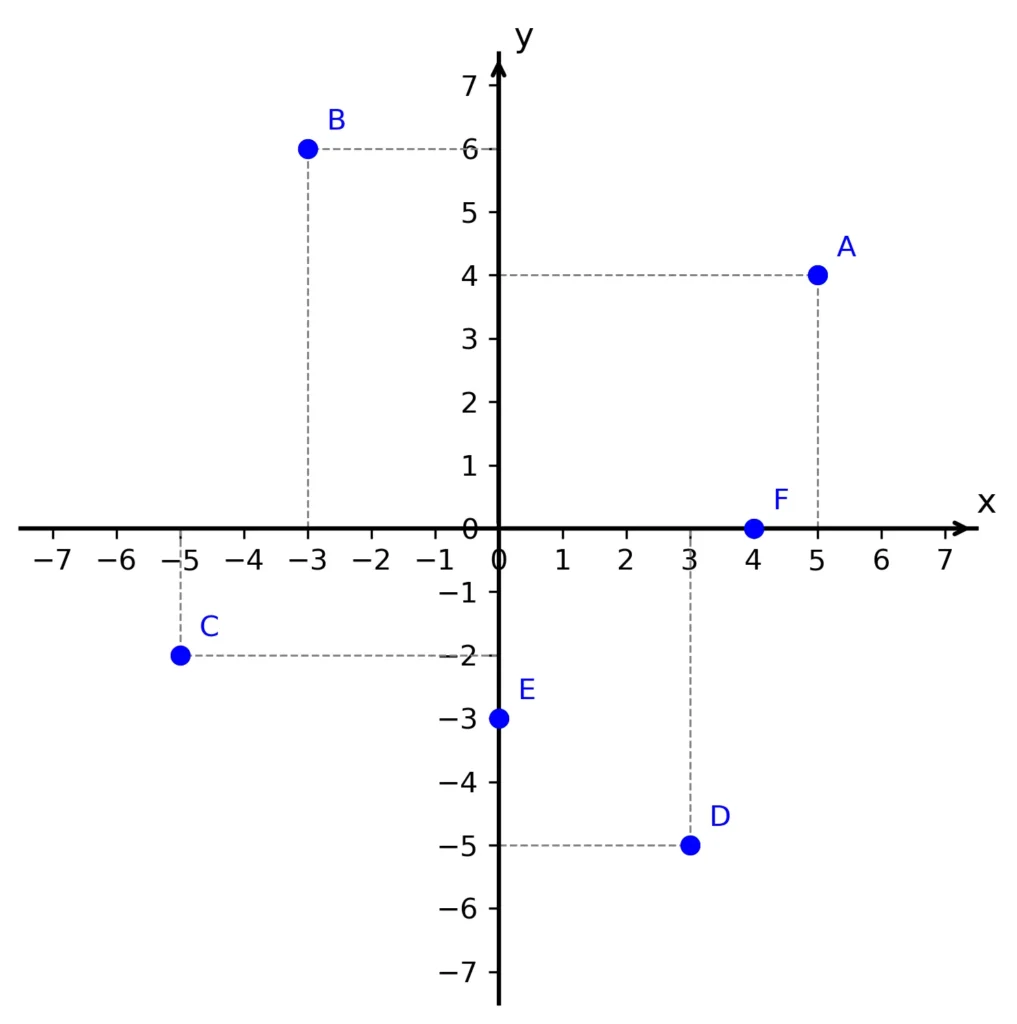
A[5; 4], B[-3; 6], C[-5, -2], D[3; -5], E[0; -3]

Řešení – viz obrázek:

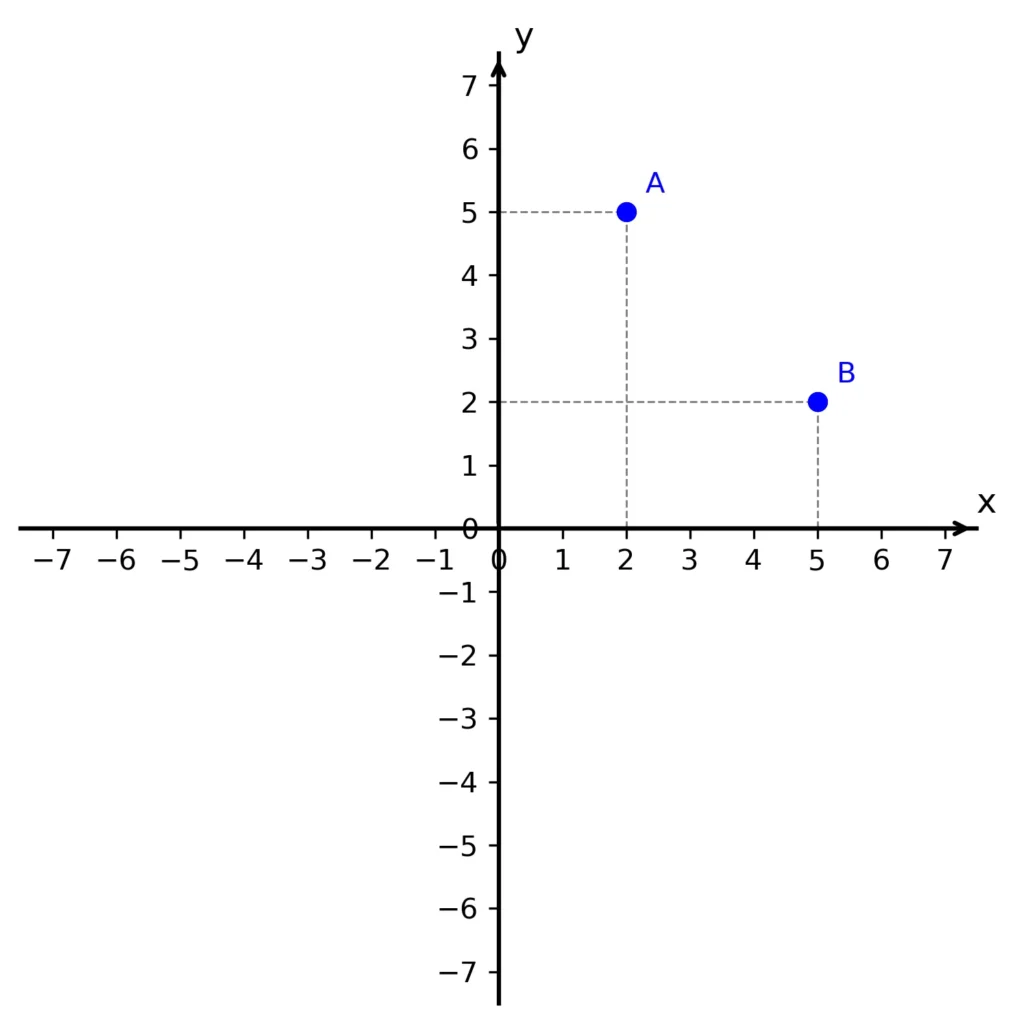
Pořadí čísel v uspořádané dvojici, která reprezentuje souřadnice bodu, je důležité a nemůžeme ho zaměnit. Například bod A o souřadnicích [2; 5] a bod B o souřadnicích [5; 2] budou v soustavě souřadnic každý na jiném místě – viz následující obrázek:

Pokud máme v kartézské soustavě souřadnic zakreslený bod A a chceme zjistit jeho souřadnice, můžeme vést tímto bodem rovnoběžky se souřadnicovými osami. Rovnoběžka s osou y protne osu x v bodě, které odpovídá nějakému číslu na této ose, jež reprezentuje právě x-ovou souřadnici tohoto bodu. Obdobně rovnoběžka s osou x protne osu y v bodě, které odpovídá nějakému číslu na této ose, jež reprezentuje právě y-ovou souřadnici tohoto bodu.

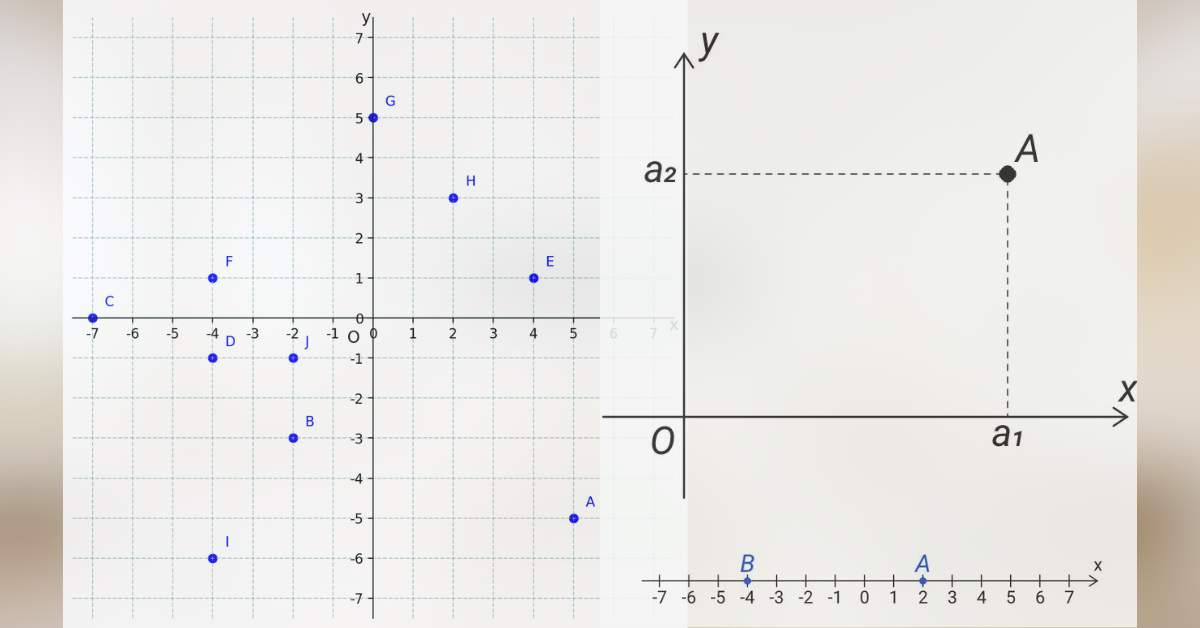
Je zvykem jednotlivé souřadnice značit malými písmeny, přičemž x-ová souřadnice se značí s dolním indexem 1 a y-ová souřadnice se značí s dolním indexem 2. Proto jednotlivé souřadnice bodu A označíme jako a₁, a₂, viz následující obrázek:

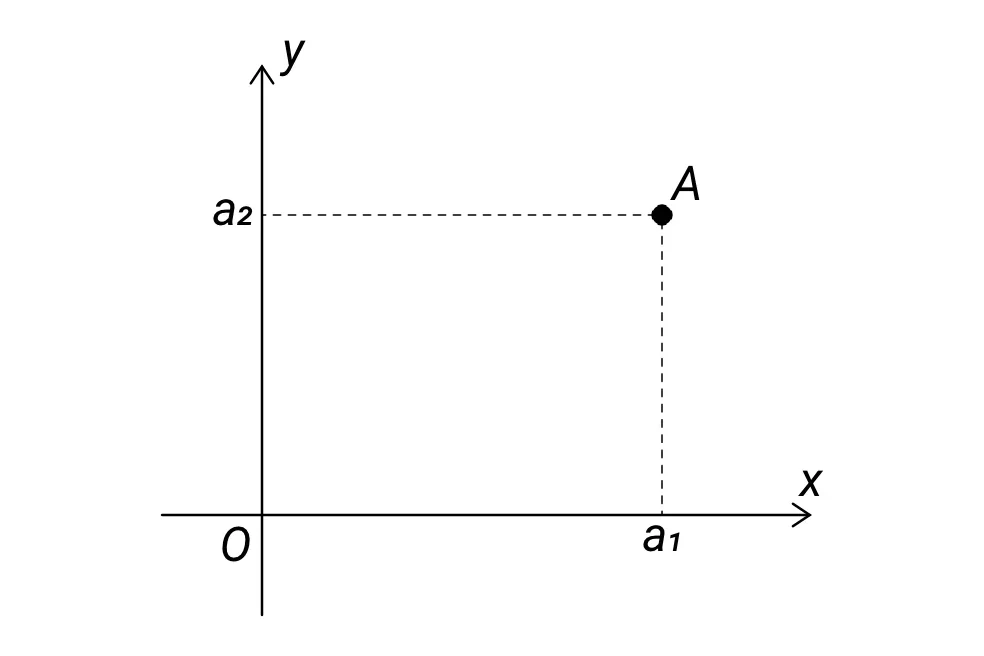
Číslo v dolním indexu tak vlastně odpovídá pořadí daného čísla v uspořádané dvojici. Obecně tedy můžeme bod A v kartézské soustavě souřadnic zapsat jako A[a₁; a₂].

Příklad 2

Zapište souřadnice všech bodů v kartézské soustavě souřadnic na obrázku:

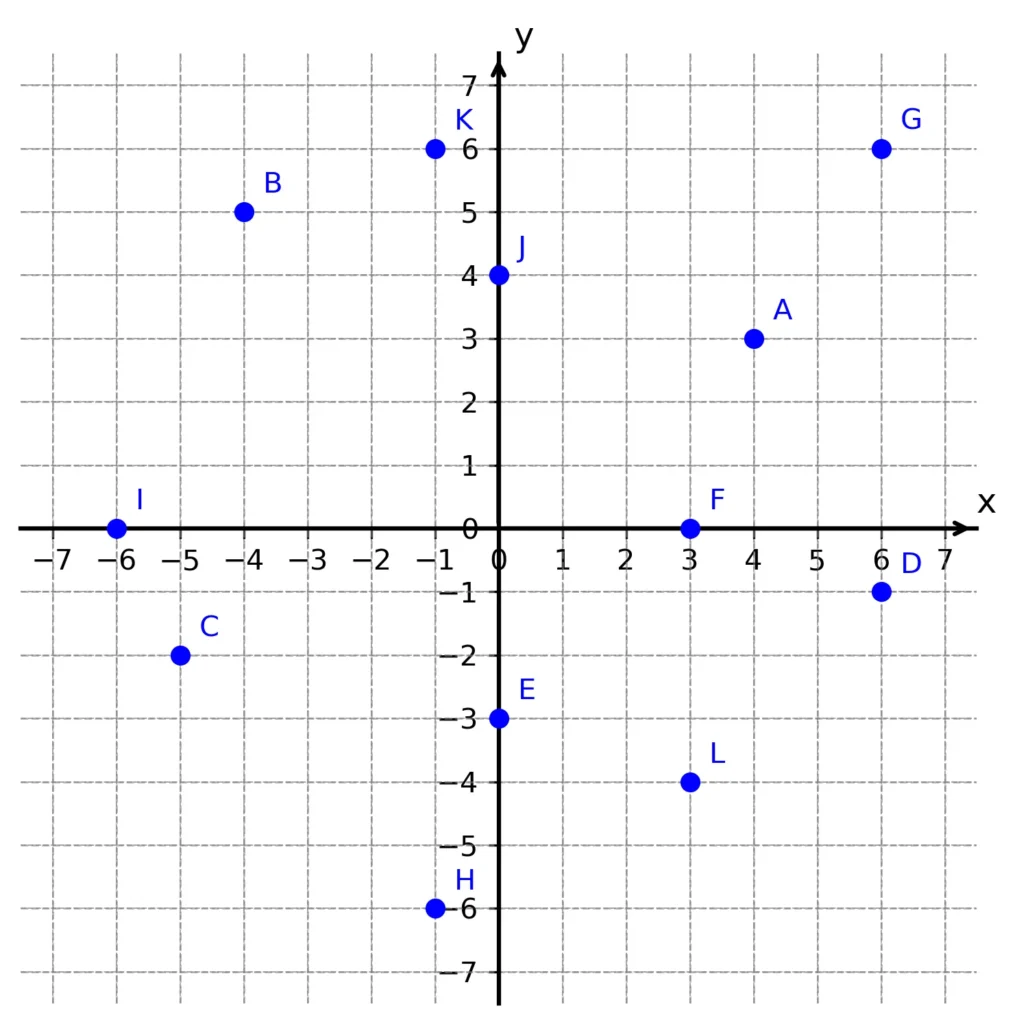
Řešení

A[4; 3], B[-4; 5], C[-5; -2], D[6; -1], E[0; -3], F[3; 0], G[6; 6], H[-1; -6], I[-6; 0], J[0; 4], K[-1; 6], L[3; -4].

Všimněte si, že všechny body, které leží na ose x, mají y-ovou souřadnici 0 a naopak všechny body, které leží na ose y, mají x-ovou souřadnici 0.

Kartézskou soustavu souřadnic budeme používat v celé analytické geometrii. Někdy budeme místo pojmu „kartézská soustava souřadnic“ psát pouze „soustava souřadnic“ nebo „souřadný systém“.

Umět zakreslovat body do kartézské soustavy souřadnic dle jejich zadaných souřadnic, a naopak umět určit jejich souřadnice z obrázku s kartézskou soustavou souřadnic, je naprosto základní a extrémně důležitá dovednost nejen pro analytickou geometrii, ale také pro funkce, práci s grafy apod.

Závěr

V tomto úvodním článku jsme se naučili zakreslovat body do kartézské soustavy souřadnic v rovině, nebo jejich souřadnice z obrázku této soustavy určit, což je fundamentální dovednost pro mnoho matematických oblastí.

V následujícím článku se podíváme na souřadnice v prostoru.