Nerovnice v součinovém tvaru - Matematika nejen pro střední školy

V předchozím článku jsme se zabývali soustavami lineárních nerovnic.

V tomto článku se budeme věnovat nerovnicím v součinovém tvaru, které mají podobný tvar, jako rovnice v součinovém tvaru, pouze místo znaku rovnosti je v nich některý ze znaků nerovnosti ($ <, >, \leqq, \geqq $). Půjde tedy o nerovnice tvaru „součin dvou nebo více činitelů je menší než (větší než, menší nebo rovno, větší nebo rovno) nula“, nebo o nerovnice, které lze na tento tvar převést.

Současně trochu navážeme právě na předchozí článek o soustavách lineárních nerovnic, protože jeden ze způsobů řešení nerovnic v součinovém tvaru v podstatě spočívá v řešení soustav nerovnic. Také se seznámíme s přehlednou a populární metodou nulových bodů.

Různé způsoby řešení si ukážeme na příkladu, který na konci obměníme, abychom pokryli více různých situací.

Příklad

Řešte nerovnici:

$$ (x \; – \; 2)(2x + 3) > 0 $$

1. způsob řešení – soustavy nerovnic

Rozbor

Vycházíme z toho, že když vynásobíme dvě čísla, tak o tom, zda bude výsledek kladný nebo záporný, rozhodují jejich znaménka. Možná si pamatujete ze základní školy následující tabulku:

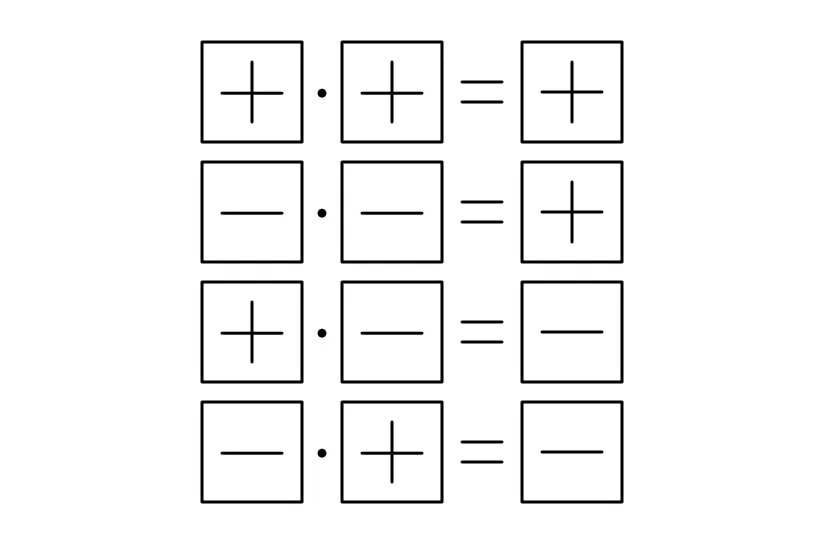
Tato tabulka nám říká, že když vynásobíme kladné číslo kladným číslem, nebo záporné číslo záporným číslem, výsledkem bude kladné číslo. A když vynásobíme kladné číslo záporným číslem, nebo záporné číslo kladným číslem, výsledkem bude záporné číslo. Jinými slovy dvě stejná znaménka nám při násobení dají kladný výsledek, zatímco dvě různá znaménka nám při násobení dají záporný výsledek.

Na tomto principu je založen tento způsob řešení, pouze nenásobíme čísla, ale závorky.

Výraz na levé straně naší nerovnice má být větší než 0, tzn. že má být kladný. To nastane tehdy, když obě závorky budou buď kladné – tedy větší než 0, nebo obě závorky budou záporné – tedy menší než 0.

Číslo x je tedy řešením naší nerovnice právě tehdy když:

$ x \; – \; 2 > 0 $ a zároveň $ 2x + 3 > 0 $

nebo

$ x \; – \; 2 < 0 $ a zároveň $ 2x + 3 < 0 $

V článku o soustavách lineárních nerovnic jsme psali, že jejich řešením jsou taková čísla, která splňují obě (nebo více) nerovnice zároveň. Proto je číslo x řešením naší nerovnice právě tehdy, když je řešením některé ze soustav lineárních nerovnic daných právě těmi řádky, které jsme napsali výše, tedy:

\begin{align*}
x \; – \; 2 &> 0 \\
2x + 3 &> 0
\end{align*}

nebo:

\begin{align*}
x \; – \; 2 &< 0 \\
2x + 3 &< 0
\end{align*}

Řešení

Z první soustavy dostaneme:

\begin{align*} x \; – \; 2 &> 0 \qquad |+2 \\ x &> 2 \end{align*}

\begin{align*} 2x + 3 &> 0 \qquad |-3 \\ 2x &> -3 \qquad |:2 \\ x &> -\frac{3}{2} \end{align*}

Odpovídající interval pro řešení $ x > 2 $ první nerovnice této první soustavy je $ (2; +\infty) $. Odpovídající interval pro řešení $ x > -\frac{3}{2} $ druhé nerovnice této první soustavy je $ \big({-}\frac{3}{2}; +\infty\big) $. Řešení celé soustavy je průnikem obou těchto intervalů. Označme ho K₁. Pak bude platit:

\[ K_1 = (2; +\infty) \cap \bigg({-}\frac{3}{2}; +\infty\bigg) = (2; +\infty) \]

Viz následující obrázek:

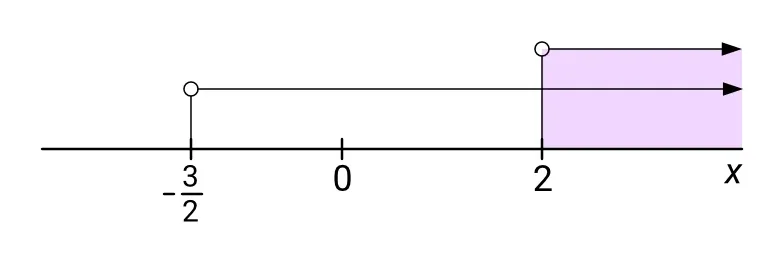
Z druhé soustavy dostaneme:

\begin{align*} x \; – \; 2 &< 0 \qquad |+2 \\ x &< 2 \end{align*}

\begin{align*} 2x + 3 &< 0 \qquad |-3 \\ 2x &< -3 \qquad |:2 \\ x &< -\frac{3}{2} \end{align*}

Odpovídající interval pro řešení $ x < 2 $ první nerovnice této druhé soustavy je $ (-\infty; 2) $. Odpovídající interval pro řešení $ x < -\frac{3}{2} $ druhé nerovnice této druhé soustavy je $ \big(-\infty; -\frac{3}{2}\big) $. Řešení celé soustavy je průnikem obou těchto intervalů. Označme ho K₂. Pak bude platit:

\[ K_2 = (-\infty; 2) \cap \bigg({-}\infty; -\frac{3}{2}\bigg) = \bigg({-}\infty; -\frac{3}{2}\bigg) \]

Viz následující obrázek:

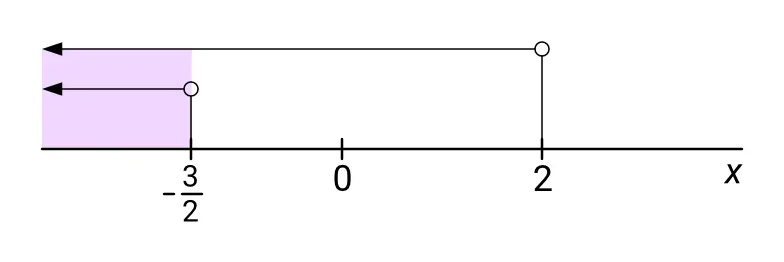
Množinou K všech řešení celé nerovnice je sjednocení množin (intervalů) řešení obou soustav:

\[ K = K_1 \cup K_2 = \bigg({-}\infty; -\frac{3}{2}\bigg) \cup (2; +\infty) \]

Viz následující obrázek:

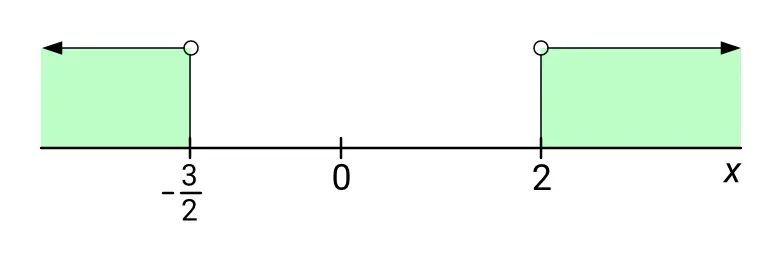
Když jsme na začátku tohoto způsobu řešení dělali rozbor úlohy, používali jsme spojky „a zároveň“ a „nebo“. Zapamatujte si: Kde je spojka „a zároveň“, tam se dělá průnik, kde je spojka „nebo“, tam se dělá sjednocení.

2. způsob řešení – metoda nulových bodů

Naše nerovnice

$$ (x \; – \; 2)(2x + 3) > 0 $$

se skládá ze dvou závorek, z nichž každá obsahuje lineární dvojčlen. Lineární dvojčlen je výraz ve tvaru $ ax + b $, kde a, b jsou reálná čísla a x je neznámá. Jinými slovy je to výraz, kde v jednom členu máme nějakou proměnnou či neznámou v první mocnině (bez exponentu) a ve druhém členu „holé“ číslo.

Nulový bod lineárního dvojčlenu je takové číslo, které po dosazení za neznámou způsobí, že tento dvojčlen bude mít hodnotu nula.

Nulový bod lineárního dvojčlenu $ x \; – \; 2 $ z první závorky naší nerovnice je číslo 2, protože když do něj toto číslo dosadíme za neznámou x, bude mít hodnotu nula. Obdobně nulový bod lineárního dvojčlenu $ 2x + 3 $ z druhé závorky naší nerovnice je číslo $ -\frac{3}{2} $, protože když do něj toto číslo dosadíme za neznámou x, bude mít hodnotu nula.

Kdybychom nemohli přijít na nulový bod daného lineárního dvojčlenu zpaměti, můžeme si ho spočítat tak, že si z tohoto dvojčlenu sestavíme rovnici, kdy ho položíme rovno nule. Například nulový bod zmíněného dvojčlenu $ 2x + 3 $ můžeme spočítat takto:

\begin{align*} 2x + 3 &= 0 \qquad |-3 \\ 2x &= -3 \qquad |:2 \\ x &= -\frac{3}{2} \end{align*}

Nulový bod daného lineárního dvojčlenu rozdělí všechna reálná čísla na dva intervaly, v nichž bude mít tento dvojčlen stále stejné znaménko. Pokud budeme např. do lineárního dvojčlenu $ x \; – \; 2 $ s nulovým bodem 2 dosazovat za x čísla menší než 2, tzn. čísla z intervalu $ (-\infty; 2) $, dostaneme vždy záporný výsledek, zatímco pokud budeme do tohoto dvojčlenu dosazovat za x čísla větší než 2, tzn. čísla z intervalu $ (2; +\infty) $, dostaneme vždy kladný výsledek.

2. krok – sestavíme tabulku intervalů a nulových bodů

Nulové body nám rozdělí množinu všech reálných čísel na o jeden víc intervalů, než kolik máme nulových bodů. V našem případě máme dva nulové body, které rozdělí množinu reálných čísel na tři intervaly – viz následující obrázek:

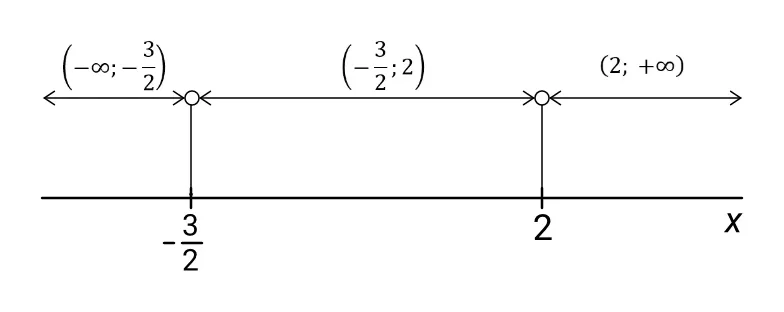
Sestavíme tabulku, jejíž sloupce budou tvořeny těmito intervaly a nulovými body uspořádanými od nejmenších hodnot po největší, řádky budou tvořeny jednotlivými dvojčleny naší nerovnice, a a poslední řádek jejich součinem – tedy celou levou stranou této nerovnice.

Do jednotlivých buněk druhého a třetího řádku napíšeme, zda bude daný dvojčlen v příslušném intervalu nebo pro příslušný nulový bod kladný (bude mít znaménko plus) nebo záporný (bude mít znaménko minus) nebo nulový.

Můžete to dělat tak, že si vymyslíte libovolné číslo v daném intervalu, dosadíte ho do dvojčlenu a pokud vám vyjde kladný výsledek, napíšete plus, pokud záporný, napíšete minus, a pokud vám vyjde nula, napíšete nulu.

Do posledního řádku tabulky pak napíšete výsledné znaménko nebo nulu, podle předchozích dvou řádků, které se vynásobí. Vzpomínáte na tabulku násobení znamének ze začátku tohoto článku? Tak přesně tímto způsobem výsledné znaménko stanovíte (dvě stejná znaménka dají plus, dvě opačná znaménka dají minus, a nula krát cokoli dá nulu).

Výsledná tabulka bude vypadat takto:

$ x $	$ \big({-}\infty; -\frac{3}{2}\big) $	$ -\frac{3}{2} $	$ \big({-}\frac{3}{2}; 2\big) $	$ 2 $	$ (2; +\infty) $
$ x \; – \; 2 $	$ – $	$ – $	$ – $	$ 0 $	$ + $
$ 2x + 3 $	$ – $	$ 0 $	$ + $	$ + $	$ + $
$ (x \; – \; 2)(2x + 3) $	$ + $	$ 0 $	$ – $	$ 0 $	$ + $

Poznámka – jak si určit tato znaménka rychle a snadno: Když budete určovat znaménko např. pro lineární dvojčlen $ x \; – \; 2 $ v intervalu $ \big({-}\infty; -\frac{3}{2}\big) $, tak si zvolíte za x libovolné číslo mezi minus nekonečnem a minus třemi polovinami. Aby se vám to dělalo co nejlépe, zvolte si nějaké jednoduché číslo a klidně extrémní, třeba $ -1000 $. Pak spočítáte, že $ 2 \cdot (-1000) = -2000 $, takže jste hluboko v mínusu, a když od tohoto výsledku odečtete dvojku, budete ještě více v mínusu, takže napíšete minus. Pro určení znaménka pro stejný dvojčlen v intervalu $ \big({-}\frac{3}{2}; 2) $ si za x můžete dosadit třeba nulu a vyjde vám $ 0 \; – \; 2 = -2 $, takže jste stále v minusu a napíšete opět minus. A pro interval $ (2; +\infty) $ si můžete dosadit za x třeba číslo $ 1000 $. $ 2 \cdot 1000 = 2000 $, takže jste vysoce v plusu, a když od tohoto výsledku odečtete číslo 2, tak to určitě nebude stačit na to, abyste klesli z plusu do mínusu, takže napíšete plus.

Všimněte si, že když si budete prohlížet znaménka například v druhém řádku (odpovídajícímu prvnímu dvojčlenu) zleva doprava, uvidíte nejdřív samá znaménka minus, která se v určitém čísle „vyhoupnou“ na nulu, ze které dále přeskočí do plusu, a tam už zůstanou (resp. zůstala by, kdybychom měli více intervalů). Ve třetím řádku (odpovídajícímu druhému dvojčlenu) je to podobné, ale mohlo by to být klidně opačně – nejdřív bychom měli plusy, potom nulu, a nakonec minusy.

U různých příkladů to může být různé – někdy je na začátku znaménko plus, někdy minus, ale k „přehoupnutí“ přes nulu do opačného znaménka dojde vždy jen jednou. V posledním řádku (odpovídajícímu celé levé straně nerovnice) se ale znaménko může „přehoupnout“ z plusu přes nulu do mínusu nebo naopak vícekrát.

3. krok – z posledního řádku tabulky určíme řešení

Protože výraz na levé straně naší nerovnice má být větší než nula, tzn. musí být kladný, tak řešením nerovnice je sjednocení těch intervalů, u nichž v posledním řádku tabulky vyšlo znaménko plus. Množina K kořenů naší nerovnice bude tedy vypadat takto:

\[ K = \bigg({-}\infty; -\frac{3}{2}\bigg) \cup (2; +\infty) \]

Další varianty nerovnice

Kdybychom v naší nerovnici

$$ (x \; – \; 2)(2x + 3) > 0 $$

měli místo znaku nerovnosti „větší než“ jiný znak nerovnosti, tabulka s nulovými body, intervaly a znaménky by vypadala úplně stejně. Podívejme se na to, jak by vypadala řešení těchto obměněných nerovnic.

1. Rovnice se znakem nerovnosti „větší nebo rovno“, tj.:

$$ (x \; – \; 2)(2x + 3) \geqq 0 $$

Protože výraz na levé straně nerovnice má být větší nebo rovno nule, řešením jsou taková čísla x, u kterých máme v posledním řádku tabulky buď znaménko plus nebo nulu.

První interval, u nějž máme v posledním řádku tabulky znaménko plus, tedy $ \big({-}\infty; -\frac{3}{2}\big) $, končí těsně před číslem $ -\frac{3}{2} $. U samotného čísla $ -\frac{3}{2} $ máme v posledním řádku tabulky nulu, která teď rovněž patří do řešení této nerovnice. To znamená, že číslo $ -\frac{3}{2} $, které k tomuto intervalu těsně přiléhá, do něj můžeme zahrnout, čímž se stane na pravé straně uzavřeným.

Druhý interval, u nějž máme v posledním řádku tabulky znaménko plus, tedy $ (2; +\infty) $ zase těsně přiléhá k číslu 2, které teď také patří do řešení této nerovnice, takže ho můžeme do tohoto intervalu zahrnout, čímž se stane na levé straně uzavřeným.

Množina K řešení této nerovnice bude vypadat takto:

\[ K = \bigg({-}\infty; -\frac{3}{2}\bigg\rangle \cup \langle 2; +\infty) \]

2. Nerovnice se znakem nerovnosti „menší než“, tj.:

$$ (x \; – \; 2)(2x + 3) < 0 $$

Zde má být výraz na levé straně nerovnice menší než nula, tzn. záporný. Řešením jsou tedy ta čísla, pro která máme v posledním řádku tabulky znaménko minus. To je prostřední z intervalů.

Množina K řešení této nerovnice bude vypadat takto:

\[ K = \bigg({-}\frac{3}{2}; 2\bigg) \]

3. Nerovnice se znakem nerovnosti „menší nebo rovno“, tj.:

$$ (x \; – \; 2)(2x + 3) \leqq 0 $$

Čísla, pro která je výraz na levé straně nerovnice menší než nula, tzn. záporný, patří do prostředního intervalu z tabulky, ale protože do řešení nerovnice patří navíc i čísla, pro která je tento výraz roven nule, patří tam i ta čísla, pro která máme v posledním řádku tabulky zapsanou nulu, tedy čísla $ -\frac{3}{2} $ a 2. Tato čísla z obou stran těsně přiléhají ke zmíněnému intervalu. Když je do tohoto intervalu zahrneme, stane se z obou stran uzavřený.

Množina K řešení této nerovnice bude vypadat takto:

\[ K = \bigg\langle {-}\frac{3}{2}; 2\bigg\rangle \]

Všimněte si, že záměna znaku nerovnosti, kdy se použije stejný znak nerovnosti jen s tím rozdílem, že obsahuje „nebo rovno“, způsobí pouze změnu daného intervalu z otevřeného na uzavřený nebo polouzavřený.

Závěr

V tomto článku jsme si probrali nerovnice v součinovém tvaru a ukázali jsme si dvě základní metody jejich řešení. Seznámili jsme se s často používanou metodou nulových bodů, která se nám bude hodit ještě u dalších typů nerovnic.

V následujícím článku se podíváme na nerovnice v podílovém tvaru.