V předchozím článku jsme si probrali několik příkladů, v nichž se používá Pythagorova věta.
V tomto článku se podíváme na Thaletovu větu, které se též týká pravoúhlého trojúhelníku.
Thaletova kružnice
Thaletovu větu nejlépe pochopíme, když si nakreslíme tzv. Thaletovu kružnici: Sestrojíme kružnici a přímku tak, aby procházela středem této kružnice. Přímka protne kružnici ve dvou bodech, které můžeme označit např. jako A a B. Tyto body budou tvořit průměr naší kružnice.
Když si nyní na kružnici zvolíme libovolný bod X, který nebude splývat s bodem A ani s bodem B, a sestrojíme trojúhelník tak, že spojíme náš bod X s body A a B, tak tento trojúhelník bude pravoúhlý, přičemž pravý úhel bude právě u bodu X.
Protože bod X jsme si zvolili libovolně, znamená to, že je úplně jedno, kde přesně na kružnici bude – příslušný trojúhelník bude zkrátka pravoúhlý vždy.
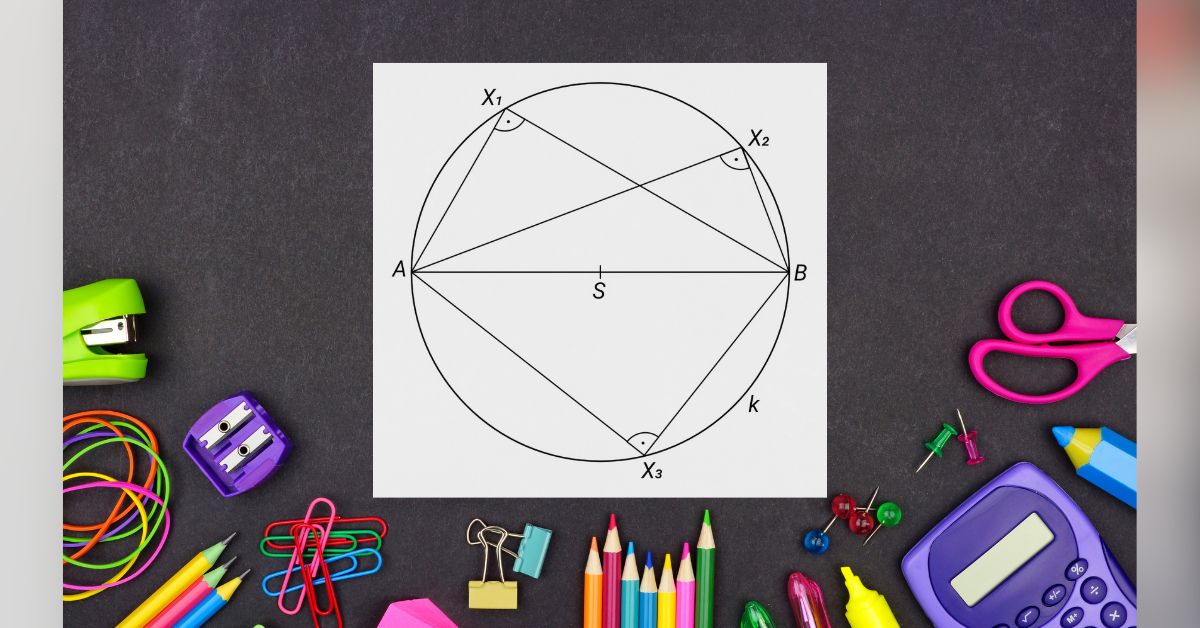
Podívejme se na následující obrázek:
Je na něm kružnice k se středem S a průměrem AB. Na této kružnici jsou libovolně zvolené body X1, X2 a X3. Podle Thaletovy věty je každý z úhlů AX1B, AX2B a AX3B pravý, tzn. že má velikost 90°.
Nyní můžeme vyslovit definici Thaletovy věty:
Všechny úhly AXB, kde X je libovolný bod kružnice různý od koncových bodů A, B jejího průměru, jsou pravé.
Ukažme si jeden příklad, kde je potřeba znát Thaletovu větu:
Příklad 1
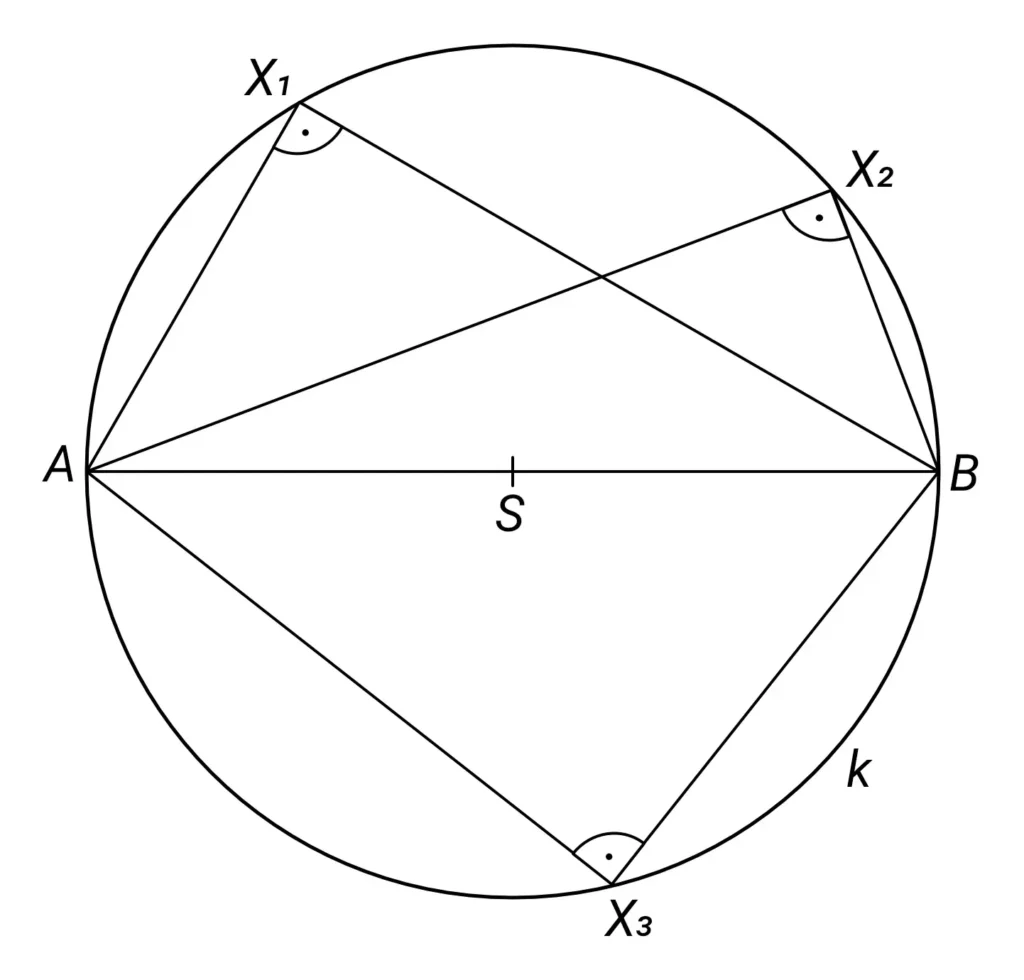
V kružnici k se středem S a poloměrem r = 7 cm jsou dány tětivy KL a LM podle následujícího obrázku:
Určete délku tětivy KM, víte-li, že tětiva LM má délku 6 cm.
Řešení
Protože tětiva KL je průměr kružnice k, je podle Thaletovy věty úhel KML pravý. Jinými slovy, kdybychom spojili body K a M, získali bychom pravoúhlý trojúhelník s pravým úhlem při vrcholu M. (Nezapomínejte, že aby platila Thaletova věta, musí v našem případě tětiva KL procházet středem kružnice a tvořit tak jehí průměr.)
Trojúhelník KLM je tedy pravoúhlý, přičemž tětiva KL je jeho přepona a tětivy LM a KM jsou odvěsny. Takže podle Pythagorovy věty platí:
$$ |KL|^2 = |KM|^2 + |LM|^2 $$
neboli:
$$ |KM|^2 = |KL|^2 \; – \; |LM|^2 $$
neboli:
$$ |KM| = \sqrt{|KL|^2 \; – \; |LM|^2} $$
Po dosazení délek tětiv KL a LM určíme délku tětivy KM (délka tětivy KL je dvakrát větší než poloměr kružnice, tedy 14 cm):
\begin{align*} |KM| &= \sqrt{14^2 \; – \; 6^2} = \sqrt{196 \; – \; 36} = \\ &= \sqrt{160} \doteq 12{,}65 \text{ cm} \end{align*}
Thaletova věta a tečna ke kružnici
Thaletova věta se často používá v konstrukčních úlohách, kde máme sestrojit tečny k dané kružnici včetně bodů dotyku.
Příklad 2
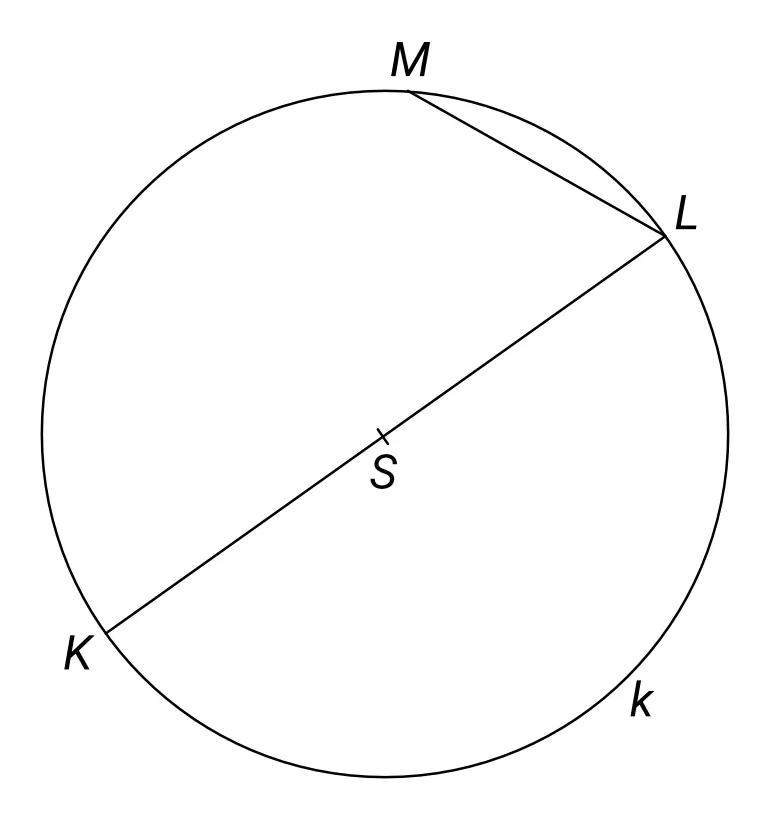
Je dána kružnice k se středem S a vně této kružnice bod P. Sestrojte na této kružnici dotykové body T1, T2 tečen vedených z bodu P.
Řešení
Podívejte se na následující obrázek:
Tečny ke kružnici jsou vždy kolmé na její poloměr. Proto jsou úhly PT1S a PT2S pravé. Jelikož jsou pravé, musí ležet na Thaletově kružnici s průměrem SP.
Sestrojíme nejdříve bod O, který bude ležet v polovině délky úsečky spojující bod P a střed kružnice S. Tento bod bude středem Thaletovy kružnice, která bude procházet právě body P a S.
Když spojíme libovolný bod ležící na Thaletově kružnici s body P a S, které tvoří její průměr, tak dostaneme pravoúhlý trojúhelník s pravým úhlem u tohoto libovolného bodu. To platí i pro body dotyku T1 a T2, které tudíž získáme jako průsečíky kružnice k a Thaletovy kružnice o průměru SP. Spojením bodu P s body dotyku T1 a T2 pak získáme tečny ke kružnici k.
Závěr
V tomto článku jsme si probrali Thaletovu větu, resp. Thaletovu kružnici, a ukázali si dva příklady jejího použití.
V následujícím článku se budeme věnovat trigonometrii pravoúhlého trojúhelníku.