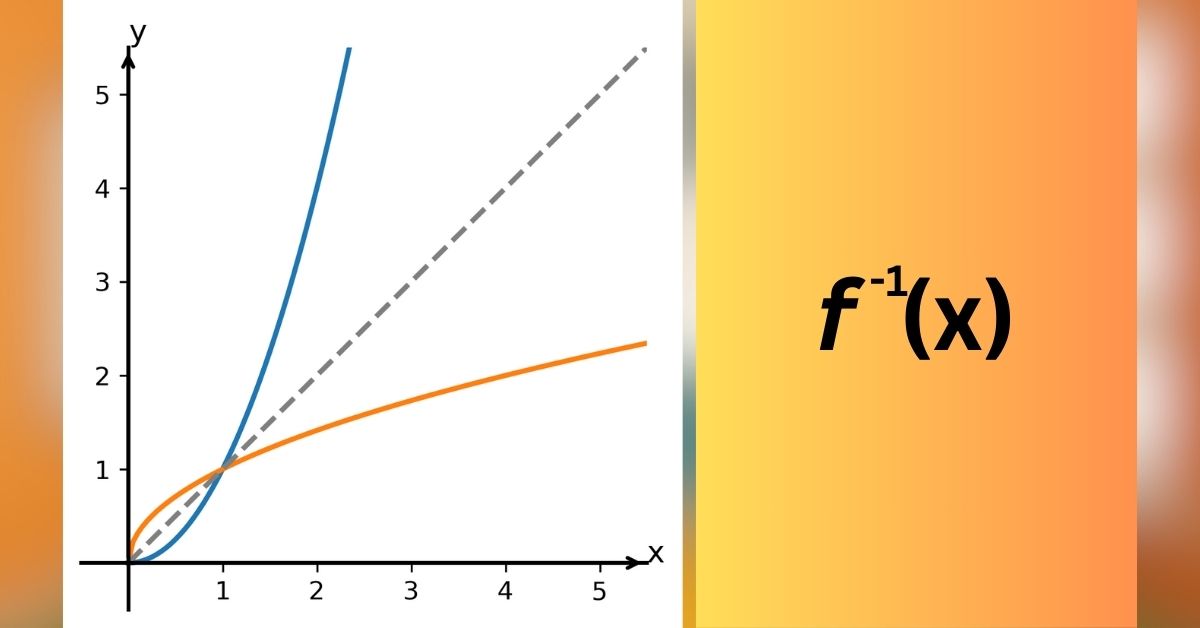V předchozím článku jsme se věnovali mocninným funkcím s celočíselným exponentem. V tomto článku uděláme od našeho „zvěřince funkcí“ malou odbočku a podíváme se na to, co znamená inverzní funkce.
Inverzní funkce totiž není jeden z dalších konkrétních druhů funkcí, tak jak je postupně probíráme v této kategorii článků, ale výsledek operace či transformace, kterou můžeme provést s každou prostou funkcí. Výsledkem této operace je jiná funkce, o které říkáme, že je inverzní k původní funkci.
Připomeňme, že prostá funkce je taková funkce, která nejen přiřazuje každému číslu x ze svého definičního oboru právě jedno číslo y z oboru hodnot (což musí splňovat každá funkce), ale platí pro ni i obráceně, že ke každému číslu y z oboru hodnot existuje právě jedno číslo x z definičního oboru. Prostá funkce je například funkce, která je na celém svém definičním oboru rostoucí nebo klesající.
Co je inverzní funkce
Představme si nějakou funkci jako „černou skříňku“, která na vstupu „přijme“ nějaké číslo x a na výstupu nám dá k němu příslušné číslo y:
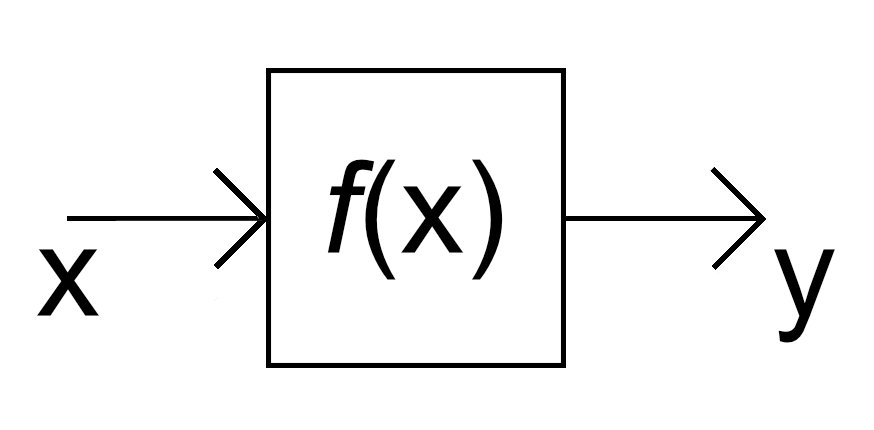
Dejme tomu, že do ní na vstupu pošleme číslo x = 2 a na výstupu dostaneme číslo y = 5.
A my bychom nyní chtěli sestrojit takovou skříňku, která bude fungovat obráceně, tzn. že na vstupu přijme to číslo x, které jsme z původní skříňky získali jako výstupní hodnotu y, a na výstupu nám dá takové číslo y, které jsme do původní skříňky poslali jako číslo x.
To v našem případě znamená, že když naše nová skříňka přijme na vstupu číslo x = 5, tak na výstupu dostaneme číslo y = 2. A chtěli bychom, aby tato nová skříňka takto fungovala pro všechna čísla, která můžeme získat na výstupu z původní skříňky.
A přesně takhle funguje inverzní funkce. Jestliže nějaká funkce přiřazuje danému číslu x z definičního oboru konkrétní číslo y z oboru hodnot, pak inverzní funkce „zpětně“ přiřazuje tomuto číslu y právě to číslo x, které jsme dosadili do původní funkce.
Pojďme si to ukázat na konkrétním příkladu.
Mějme lineární funkci danou předpisem:
$$ f(x): y = 2x \; – \; 1 $$
Vytvoříme si tabulku několika hodnot x a vypočítáme k nim příslušné hodnoty y:
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -5 | -3 | -1 | 1 | 3 | 5 |
Nyní si tyto body vyneseme do souřadného systému a sestrojíme graf:
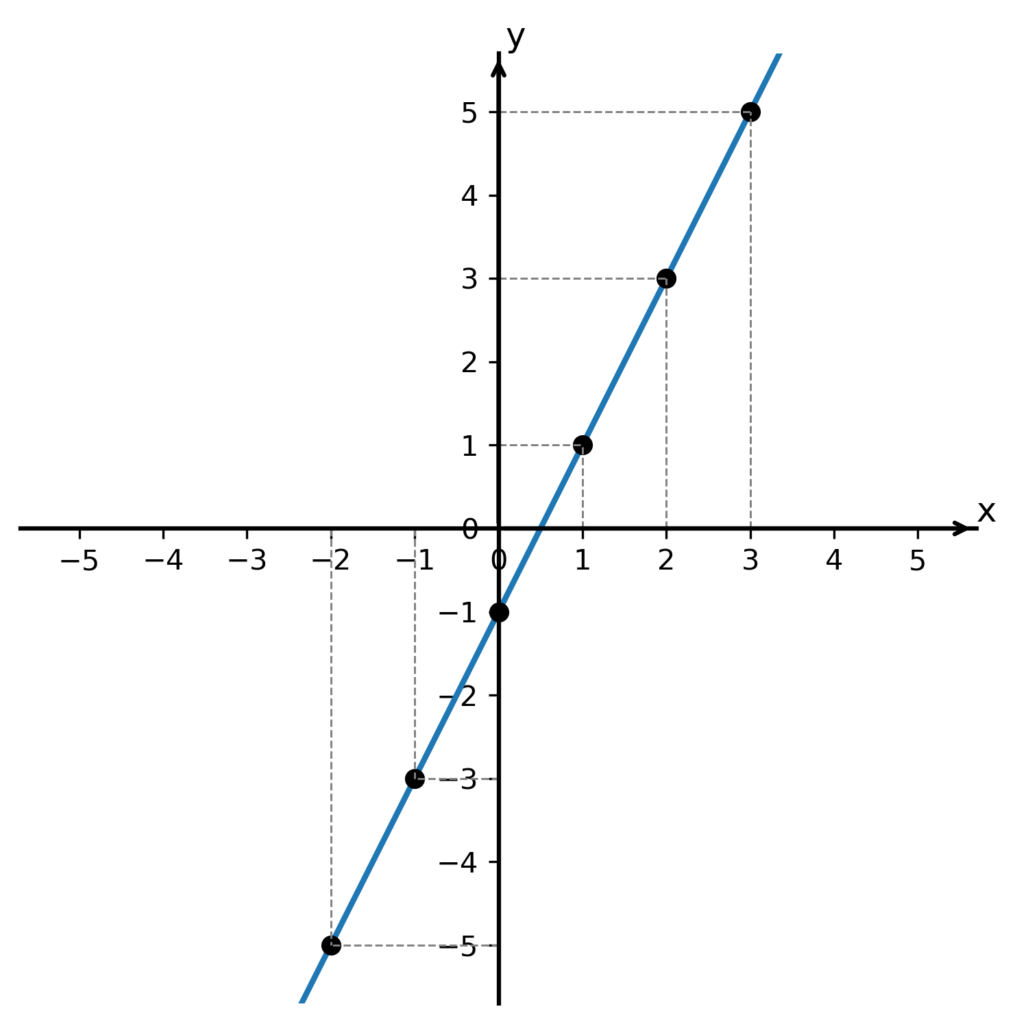
Funkce je rostoucí a tím pádem prostá. Například číslu x = 2 z definičního oboru přiřazuje číslo y = 3 z oboru hodnot, a obráceně platí, že číslo y = 3 z oboru hodnot funkce přiřazuje pouze číslu x = 2 z definičního oboru a žádnému jinému. Nebo číslu x = -1 funkce přiřazuje číslo y = -3, a obráceně platí, že číslo y = -3 funkce přiřazuje pouze číslu x = -1 a žádnému jinému.
A protože stejné pravidlo platí pro jakoukoli dvojici čísel x a y, můžeme k této funkci najít inverzní funkci, která bude fungovat „obráceně“, tzn. že hodnoty y z naší tabulky se stanou hodnotami x této naší nové funkce a hodnoty x se stanou hodnotami y. Jednoduše všechna čísla x a y prohodíme a získáme tabulku k naší hledané inverzní funkci:
| x | -5 | -3 | -1 | 1 | 3 | 5 |
| y | -2 | -1 | 0 | 1 | 2 | 3 |
A můžeme sestrojit její graf:
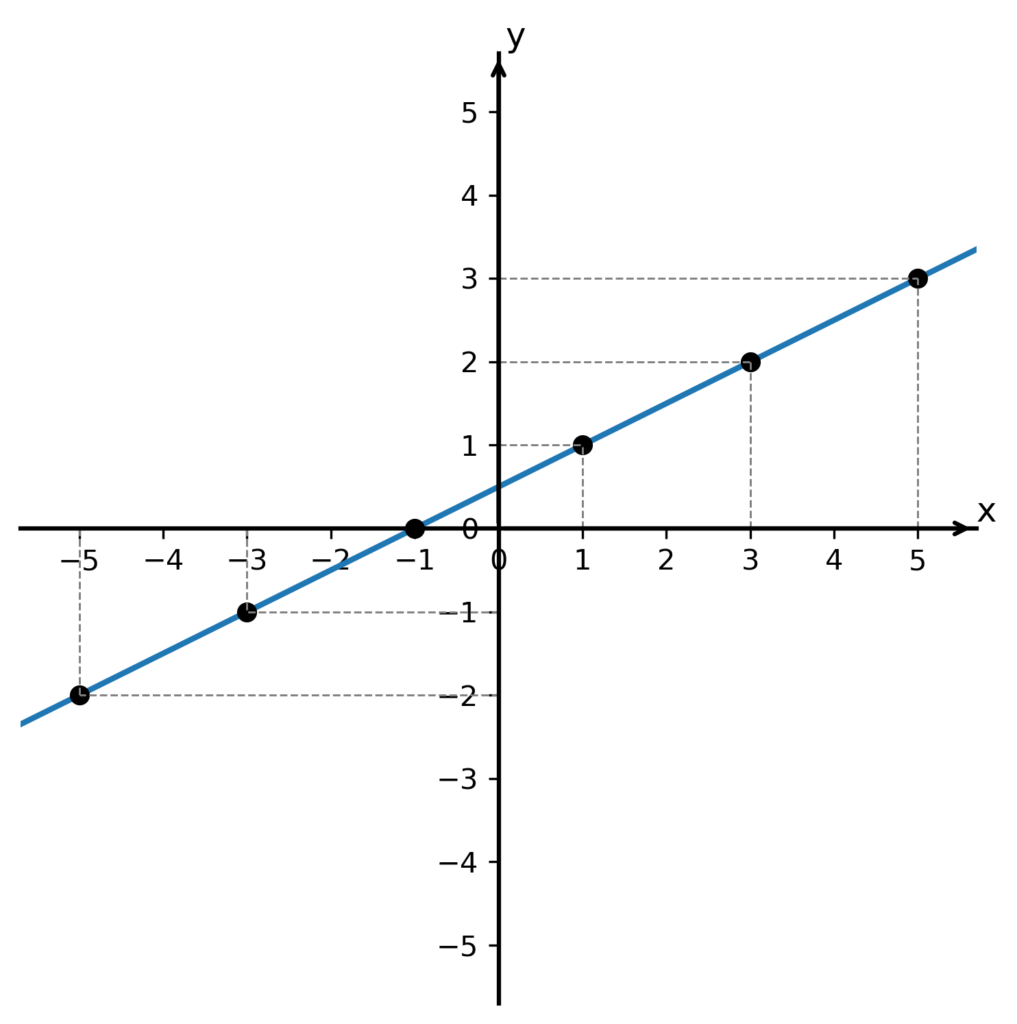
Předpis inverzní funkce
Dokázali jsme sestrojit graf inverzní funkce k naší původní funkci f jen tím, že jsme v tabulce prohodili všechny hodnoty x a y. Jak ale získáme její předpis?
Podívejme se na předpis naší funkce f:
$$ f(x): y = 2 x \; – \; 1 $$
Vidíme, že na levé straně máme proměnnou y a na pravé straně nějaký výraz obsahující proměnnou x. Nyní tento předpis vezmeme a budeme ho postupně upravovat jako rovnici, přičemž našim cílem bude dosáhnout „opačného“ tvaru – tzn. abychom na levé straně měli proměnnou x a nic jiného, a na pravé straně výraz obsahující proměnnou y:
\begin{align*}
y &= 2x \; – \; 1 \qquad |+1 \\
y + 1 &= 2x \qquad |:2 \\
\frac{y}{2} + \frac{1}{2} &= x \\
x &= \frac{1}{2}y + \frac{1}{2}
\end{align*}
Nyní v tomto předpisu zaměníme x a y, tedy všude, kde máme x, napíšeme místo něj y, a všude, kde máme y, napíšeme místo něj x:
$$ y = \frac{1}{2}x + \frac{1}{2} $$
A získali jsme předpis inverzní funkce k naší funkci f.
Inverzní funkce se značí jako „název původní funkce na mínus prvou“, v našem případě tedy $ f^{-1} $ nebo $ f^{-1}(x) $. Celý náš předpis včetně názvu inverzní funkce bude tedy vypadat takto:
$$ f^{-1}(x): y = \frac{1}{2}x + \frac{1}{2} $$
Kdybyste si nyní sestrojili graf této inverzní funkce podle jejího předpisu, byl by úplně stejný jako na obrázku výše, kde jsme pouze prohodili čísla x a y v tabulce.
Vlastnosti inverzní funkce
Stejně jako jsme v tabulce výše prohodili čísla x a y, tak platí, že se prohodí i definiční obor a obor hodnot, tedy definičním oborem inverzní funkce je obor hodnot původní funkce, a oborem hodnot inverzní funkce je definiční obor původní funkce, což můžeme matematicky vyjádřit takto:
$$ D(f^{-1}) = H(f) $$
$$ H(f^{-1}) = D(f) $$
Dalším důležitým poznatkem ohledně inverzní funkce je, že pokud máme osy souřadného systému nakreslené ve stejném měřítku, potom grafy každé původní a k ní inverzní funkce budou osově souměrné podle osy I. a III. kvadrantu – viz následující obrázek:
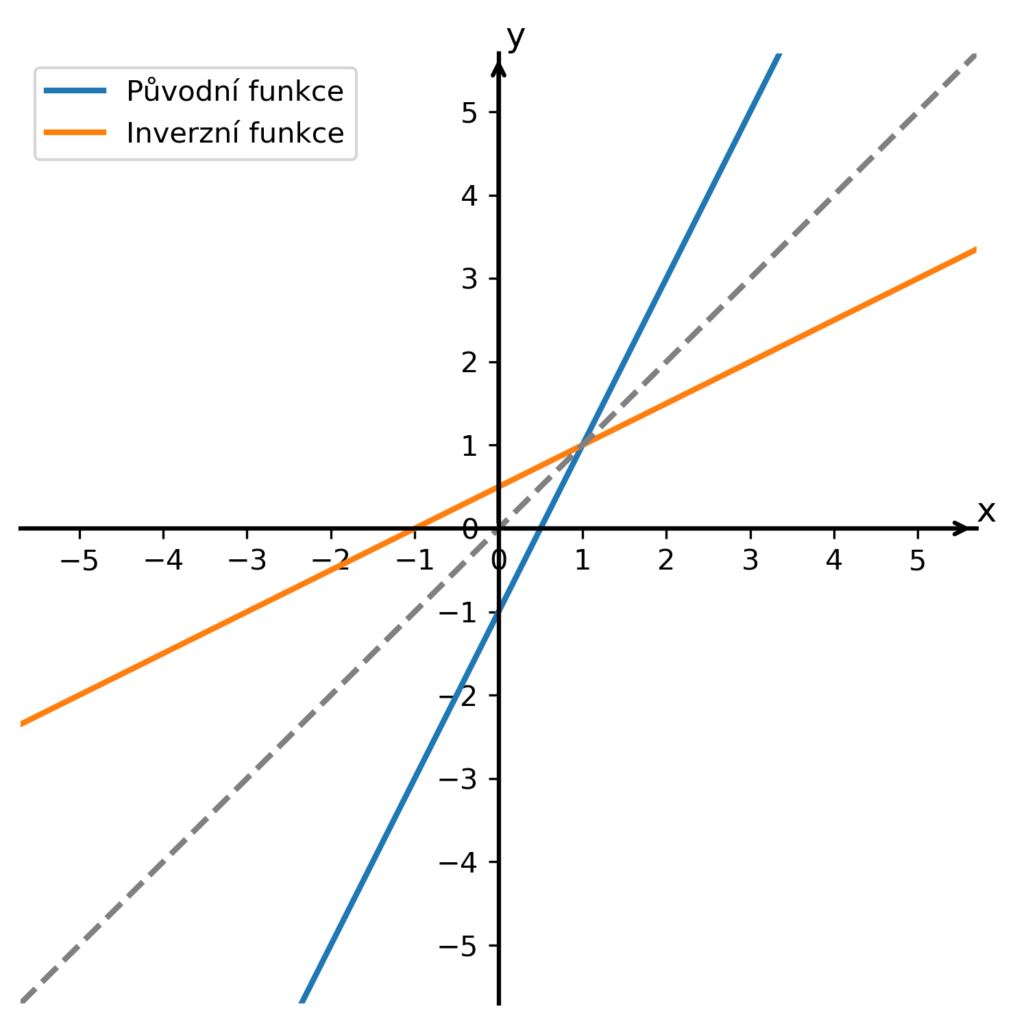
kde šedá čárkovaná čára je právě osa souměrnosti. Možná vás napadlo, co kdybychom hledali inverzní funkci k inverzní funkci. Odpověď je, že bychom dostali původní funkci, takže o každé původní a inverzní funkci můžeme říct, že jsou vzájemně inverzní.
Omezení definičního oboru u funkce, která není prostá
Na začátku článku jsme kladli důraz na to, že abychom mohli k nějaké funkci najít funkci inverzní, musí být tato funkce prostá. Ukažme si příklad funkce, která není prostá, a co se stane, když k ní budeme hledat inverzní funkci.
Takovou funkcí může být například jednoduchá kvadratická funkce s předpisem:
$$ f(x): y = x^2 $$
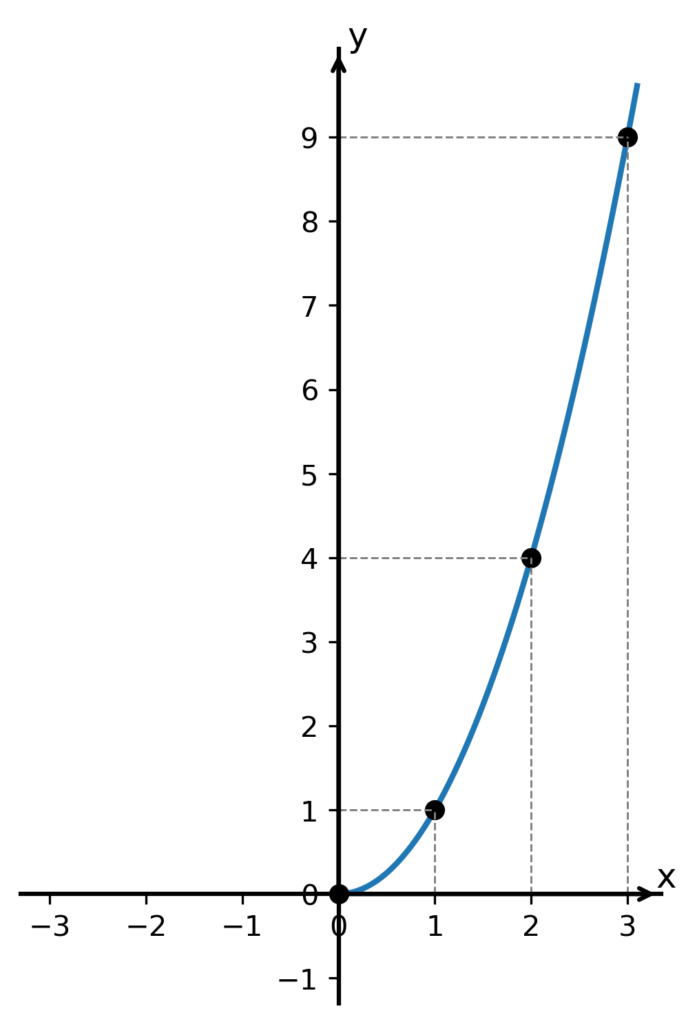
jejíž graf vypadá takto:

Tato funkce přiřazuje např. číslu x = 2 hodnotu y = 4, ale opačně nemůžeme říct, že číslo y = 4 získáme pouze dosazením čísla x = 2 do jejího předpisu, protože toto y = 4 stejně tak získáme i dosazením čísla x = -2.
Opět si představme tuto funkci jako naši „černou skříňku“ – pokud bychom sestrojili jinou skříňku, která bude fungovat opačně, tak bychom na vstupu dosadili číslo 4 a na výstupu bychom měli čísla dvě: 2 a -2, což je v rozporu s definicí funkce, protože každá funkce musí přiřazovat „vstupní“ hodnotě právě jednu hodnotu „výstupní“.
Pokud chceme najít inverzní funkci k funkci, která není prostá, musíme omezit její definiční obor na interval, na kterém prostá je. U naší funkce $ y = x^2 $ to znamená omezit její definiční obor na takový interval, na němž je funkce buď pouze klesající nebo pouze rostoucí.
Funkce je klesající na intervalu $ (-\infty; 0 \rangle $ a rostoucí na intervalu $ \langle 0; +\infty) $. Omezme tedy její definiční obor např. pouze na interval, na kterém je rostoucí. Získáme tak funkci:
$$ f(x): y = x^2 $$
s definičním oborem:
$$ D(f) = \langle 0; +\infty) $$
jejíž graf bude vypadat takto:
Vidíme, že funkce už je prostá, ale za cenu toho, že jsme zcela odstranili zápornou větev paraboly. Nyní při „zpětném přiřazení“ nikde nevznikne dvojznačnost – např. číslo y = 4 získáme pouze z čísla x = 2 a žádného jiného.
Inverzní funkci získáme tak, že její předpis upravíme stejnou metodou, jako když jsme hledali předpis inverzní funkce k lineární funkci výše. V tomto případě to znamená, že obě strany předpisu odmocníme a následně prohodíme písmena x a y:
\begin{align*}
y &= x^2 \qquad |\sqrt{} \\
\sqrt{y} &= x \\
y &= \sqrt{x}
\end{align*}
Získali jsme funkci druhá odmocnina, které se budeme věnovat v příštím článku. Sestrojme si její graf a pro srovnání si v souřadném systému ponechme i graf původní funkce:
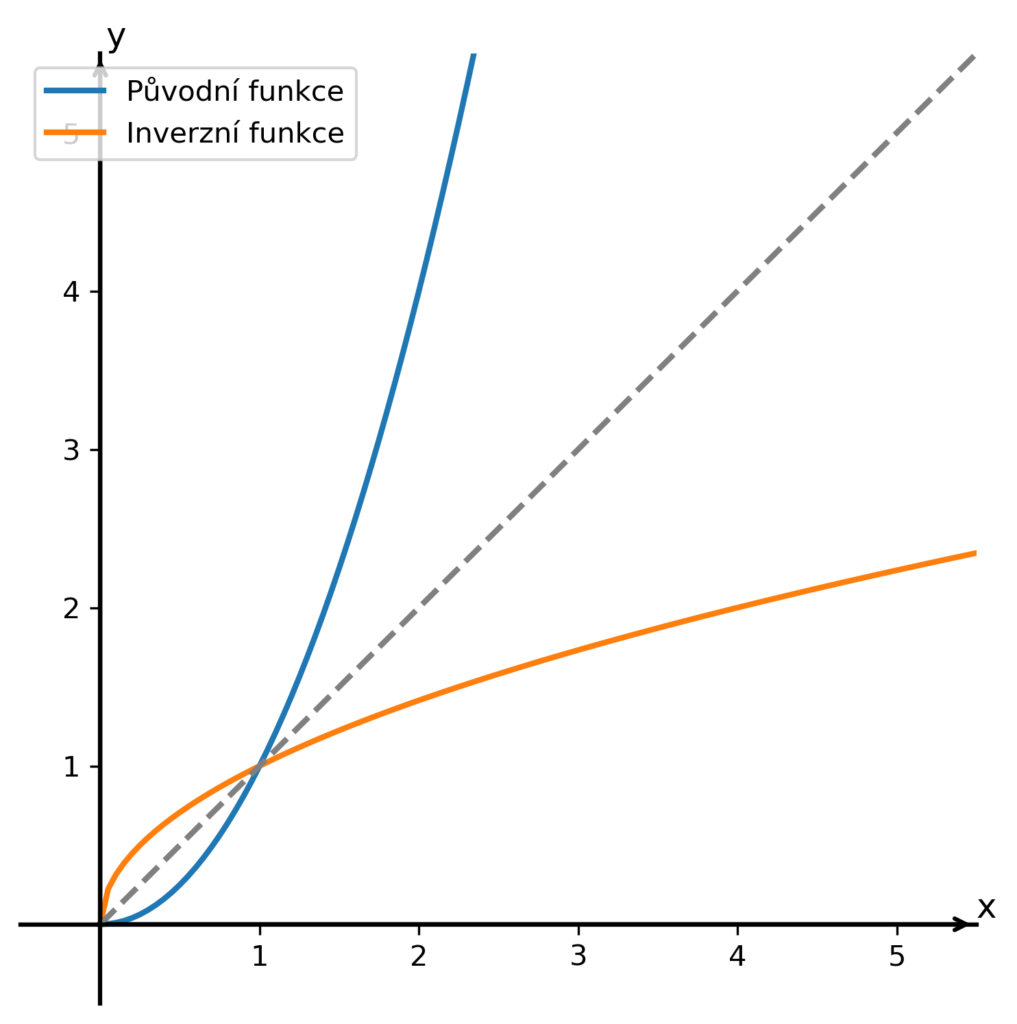
Opět můžeme vidět, že grafy původní a inverzní funkce jsou osově symetrické podle osy I. a III. kvadrantu (šedá čárkovaná čára).
Závěr
V tomto článku jsme si vysvětlili pojem inverzní funkce a ukázali si postup, jak ji najít. Získali jsme tak užitečné znalosti k následujícím článkům, ve kterých budeme pokračovat ve výčtu konkrétních druhů funkcí, které se na středních školách probírají. Některé z těchto funkcí budou totiž definovány jako inverzní k jiné funkci.
V příštím článku se budeme věnovat funkci n-tá odmocnina.