V předchozím článku jsme si probrali mocninné funkce s přirozeným exponentem. V tomto článku se podíváme na mocninné funkce s celým exponentem. To znamená, že exponent v předpisu funkce už nebude omezen pouze na přirozená – tedy celá kladná – čísla jako např. 1, 2, 3 atd., ale může ho tvořit i 0 nebo číslo celé záporné – např. -1, -2, -3 atd.
Mocninné funkce s nulovým nebo záporným celým exponentem
Protože i přirozená čísla patří mezi čísla celá a příslušným funkcím jsme se věnovali právě v minulém článku, budeme se nyní zabývat těmi mocninnými funkcemi, u nichž je exponent nulový nebo záporný.
n = 0
Jako první se podívejme na mocninnou funkci, jejíž exponent je 0. Její předpis vypadá následovně:
$$ f(x): y = x^0 $$
Funkční hodnotu y tedy získáme tak, že vezmeme nějaké číslo x z definičního oboru funkce a umocníme ho na nultou. Na tomto místě je vhodné připomenout, že jakékoli číslo kromě nuly umocněné na nultou se vždy rovná jedné, tedy platí:
$ x^0 = 1 $ … pro všechna reálná čísla $ x \neq 0 $.
Jediné číslo, které nemůžeme umocnit na nultou, je nula. Výraz $ 0^0 $ z matematického hlediska nemá smysl.
Grafem funkce $ y = x^0 $ tedy bude vodorovná přímka rovnoběžná s osou x, která bude přerušená právě v čísle 0, protože, jak již bylo řečeno, toto číslo umocnit na nultou nelze:

Jde vlastně o část konstantní funkce $ y = 1 $ s definičním oborem $ R \; – \; \{0\} $.
Mocninné funkce se záporným celým exponentem
Obecný předpis mocninné funkce se záporným celým exponentem je:
$$ f(x): y = x^{-n} $$ kde $ n \in N $, tedy číslo n je číslo přirozené a znaménko minus před ním z něj udělá číslo záporné – v našem případě záporný exponent.
Počítání mocnin se záporným exponentem
Zde je zase vhodné připomenout, jak se počítají mocniny se záporným celým exponentem.
Jestliže máme umocnit např. $ 2^3 $, víme, že musíme číslo 2 vynásobit sebou samým třikrát, takže:
$$ 2^3 = 2 \cdot 2 \cdot 2 = 8 $$
Jak ale umocníme číslo 2 např. na minus třetí? Těžko si dovedeme představit, jak vynásobit číslo 2 sama sebou minus třikrát. 🙂
Musíme na to jít trochu jinak: číslo, které máme umocnit záporným exponentem, napíšeme do jmenovatele zlomku, v jehož čitateli bude jednička, a poté ho umocníme stejně, jako by tento exponent byl kladný, tzn. že použijeme následující vzorec:
$$ x^{-n} = \frac{1}{x^n} $$
A umocnit jmenovatel zlomku kladným celým exponentem umíme.
Ukažme si pár příkladů:
$$ 2^{-2} = \frac{1}{2^2} = \frac{1}{4} $$
$$ 2^{-3} = \frac{1}{2^3} = \frac{1}{8} $$
$$ 2^{-4} = \frac{1}{2^4} = \frac{1}{16} $$
$$ 3^{-2} = \frac{1}{3^2} = \frac{1}{9} $$
$$ 4^{-3} = \frac{1}{4^3} = \frac{1}{64} $$
Příklady mocninných funkcí se záporným celým exponentem
Pojďme si nyní sestrojit několik grafů mocninných funkcí se záporným celým exponentem. Grafem každé mocninné funkce se záporným celým exponentem je hyperbola stupně n+1. Pro n = 1 je to rovnoosá hyperbola, kterou známe z nepřímé úměrnosti.
n = 1
Začneme u exponentu -1. Předpis funkce bude tedy následující:
$$ f(x): y = x^{-1} $$
Podle pravidla pro počítání mocnin se záporným exponentem ho můžeme upravit takto:
$$ f(x): y = \frac{1}{x^1} \rightarrow y = \frac{1}{x} $$
Dospěli jsme ke stejnému předpisu funkce jako u nepřímé úměrnosti s koeficientem k = 1, což znamená, že v případě mocninné funkce dané předpisem $ y = x^{-1} $ se skutečně jedná o nepřímou úměrnost. A tuto funkci již známe – jejím grafem je rovnoosá hyperbola:

Dále vidíme, že nezávisle proměnná x tvoří v tomto upraveném zápisu $ y = \frac{1}{x^1} $ jmenovatel zlomku, takže do předpisu funkce nemůžeme za x dosadit nulu. To samé bude platit, když bude exponent ve jmenovateli zlomku 2, 3, 4 atd., protože např. $ 0^2 $ se stále rovná nule. A nulu jsme nemohli dosadit ani do předpisu mocninné funkce s nulovým exponentem $ y = x^0 $.
To ale znamená, že definiční obor každé mocninné funkce s nulovým nebo se záporným celým exponentem tvoří všechna reálná čísla kromě čísla 0, tedy platí:
$$ D(f) = R \; – \; \{0\} $$
n = 2
Nyní sestrojíme graf mocninné funkce s exponentem -2. Její předpis bude následující:
$$ f(x): y = x^{-2} $$
Podle pravidla pro počítání se zápornými exponenty ho můžeme upravit takto:
$$ f(x): y = \frac{1}{x^2} $$
Vytvoříme si tabulku s několika kladnými a stejným počtem záporných hodnot x a vypočítáme k nim příslušné hodnoty y:
| x | -2 | -1 | $ -\frac{1}{2} $ | $ \frac{1}{2} $ | 1 | 2 |
| y | $ \frac{1}{4} $ | 1 | 4 | 4 | 1 | $ \frac{1}{4} $ |
Příslušné body, jejichž souřadnice jsou dány jednotlivými sloupci tabulky, zakreslíme do souřadného systému a proložíme jimi dvě křivky – jednu na levé straně osy y, druhou na straně pravé:
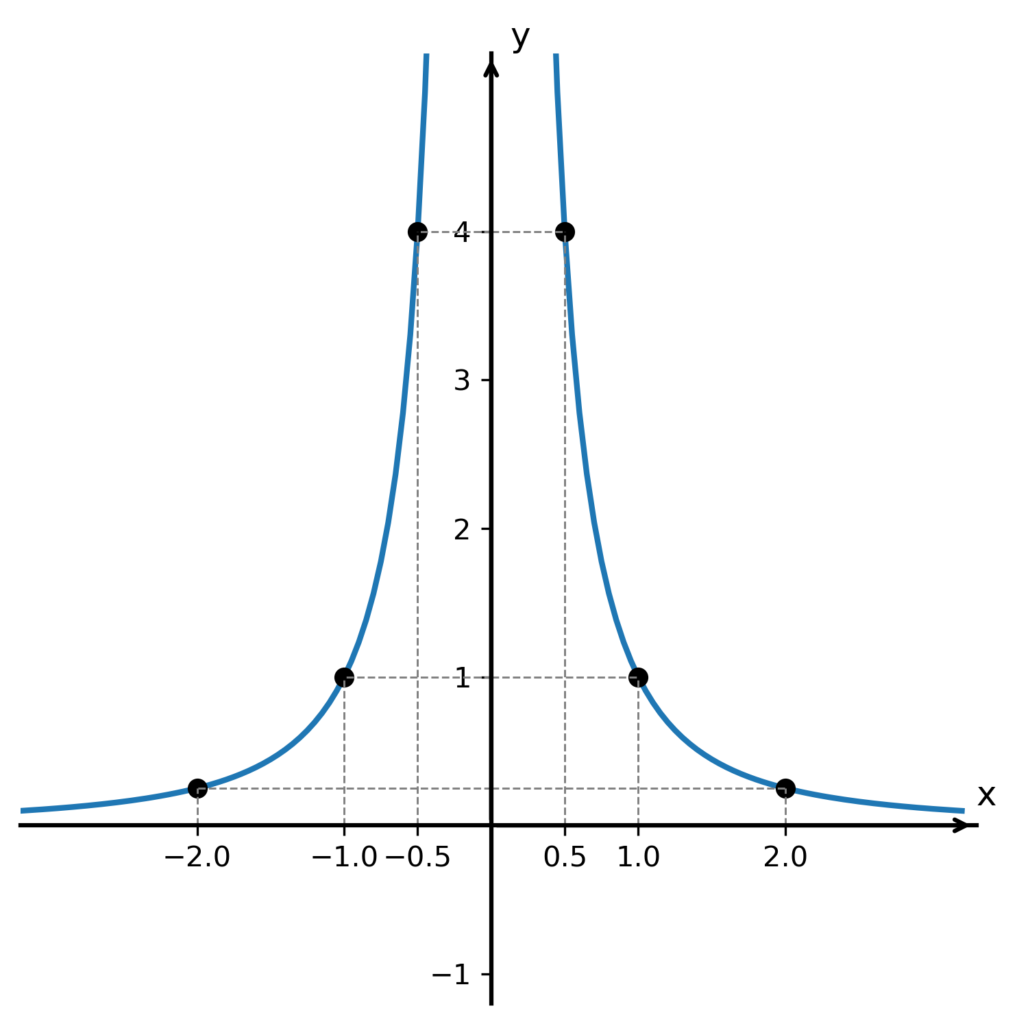
V našem aktuálním případě jde o hyperbolu druhého stupně. Vidíme, že má tendenci se přibližovat k ose x rychleji než k ose y souřadného systému. Například pro x = 2 je funkční hodnota y pouze $ \frac{1}{4} $, tedy naše hyperbola je zde vzdálená jen $ \frac{1}{4} $ jednotky od osy x. Když se oproti tomu podíváme na číslo 4 na ose y, které je dále od počátku souřadného systému, vidíme, že hyperbola je zde od této osy vzdálená stále ještě $ \frac{1}{2} $ jednotky. Na vzdálenost $ \frac{1}{4} $ by se přiblížila až v čísle y = 16.
Graf mocninné funkce se záporným celým exponentem můžeme sestrojit ještě trochu jiným způsobem: vytvoříme si stejnou tabulku, jako bychom chtěli sestrojit graf mocninné funkce s příslušným kladným exponentem, a poté přidáme řádek, do kterého si zapíšeme převrácené hodnoty výpočtů získaných po umocnění hodnot x tímto kladným exponentem.
V našem aktuálním příkladu si nejdříve zvolíme exponent n = 2, takže všechna čísla umocníme na druhou, a do třetího řádku tabulky zapíšeme převrácené hodnoty těchto druhých mocnin, čímž získáme hodnoty naší funkce s exponentem n = -2. Tabulka bude vypadat takto:
| x | -2 | -1 | $ -\frac{1}{2} $ | $ \frac{1}{2} $ | 1 | 2 |
| y1 | 4 | 1 | $ \frac{1}{4} $ | $ \frac{1}{4} $ | 1 | 4 |
| y | $ \frac{1}{4} $ | 1 | 4 | 4 | 1 | $ \frac{1}{4} $ |
Do souřadného systému můžeme nakreslit grafy obou funkcí: pomocnou $ y_1 = x^2 $ a cílovou $ y = x^{-2} $ neboli $ y = \frac{1}{x^2} $:

n = 3
Do třetice si sestrojíme graf mocninné funkce se záporným celým exponentem -3.
Její předpis je následující:
$$ f(x): y = x^{-3} $$
Můžeme ho upravit na tvar:
$$ f(x): y = \frac{1}{x^3} $$
Opět si uděláme tabulku dvojic hodnot x a y:
| x | -2 | -1 | $ -\frac{1}{2} $ | $ \frac{1}{2} $ | 1 | 2 |
| y | $ -\frac{1}{8} $ | -1 | -8 | 8 | 1 | $ \frac{1}{8} $ |
Graf této funkce bude vypadat takto:
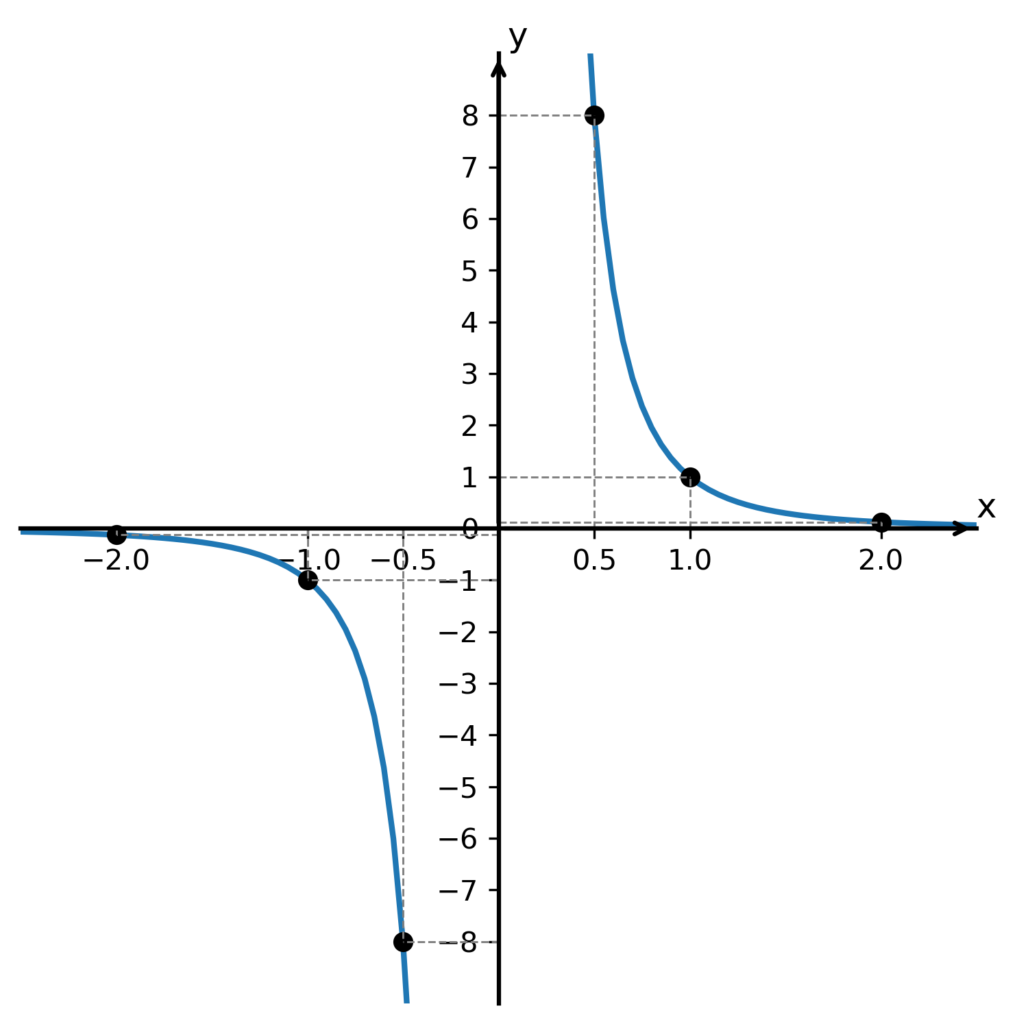
Graf má nyní jednu větev ve III. kvadrantu souřadného systému (vlevo dole). Vidíme, že se nám zde opakuje situace s mocninnými funkcemi s přirozeným exponentem. I zde platí, že pro liché exponenty n bude mít graf mocninné funkce se záporným celým exponentem větve v I. a III. kvadrantu a pro sudé exponenty n bude mít graf větve v I. a II. kvadrantu souřadného systému.
Rozdíl spočívá především v tom, že u mocninných funkcí s přirozeným exponentem byla grafem parabola n-tého stupně, zatímco u mocninných funkcí se záporným celým exponentem je to hyperbola stupně n+1.
Dále vidíme, že hyperbola z našeho posledního příkladu má ještě větší tendenci blížit se k ose x souřadného systému rychleji, než k ose y.
Vlastnosti mocninných funkcí se záporným celým exponentem
Definiční obor mocninných funkcí se záporným celým exponentem je množina všech reálných čísel kromě čísla 0, tedy:
$$ D(f) = R \; – \; \{0\} $$
Funkce nemá v žádném bodě ani minimum ani maximum.
Pokud je exponent -n lichý:
- Oborem hodnot je $ H(f) = R \; – \; \{0\} $.
- Funkce je klesající na intervalech $ (-\infty; 0) $ a $ (0; +\infty) $.
- Není ani zdola ani shora omezená.
- Je lichá.
Pokud je exponent -n sudý:
- Oborem hodnot je $ H(f) = (0; +\infty) = R^{+} $
- Funkce je rostoucí na intervalu $ (-\infty; 0) $ a klesající na intervalu $ (0; +\infty) $
- Je zdola omezená.
- Je sudá.
Možná vás napadlo, jak je možné, že žádná mocninná funkce se záporným exponentem nemá v žádném bodě ani minimum ani maximum. U liché funkce je to zřejmé, protože jedna z větví hyperboly je ve třetím kvadrantu, kde klesá do minus nekonečna. Ale u sudé funkce jsou větve hyperboly v prvním a druhém kvadrantu a žádná z nich nikdy neklesne pod hodnotu y = 0.
Je to dáno tím, že tyto větve se směrem doleva i doprava neustále přibližují k hodnotě y = 0. Půjdeme-li např. ve směru kladné osy x (doprava), funkce bude stále klesající, ale bude klesat pomaleji a pomaleji. I když budeme na ose x hodně daleko a příslušná funkční hodnota y bude nepatrná, tak směrem ještě více do kladných hodnot x bude funkční hodnota y ještě menší.
Zkrátka ať vymyslíte jakkoli malé kladné číslo, vždycky existuje ještě menší kladné číslo. 🙂
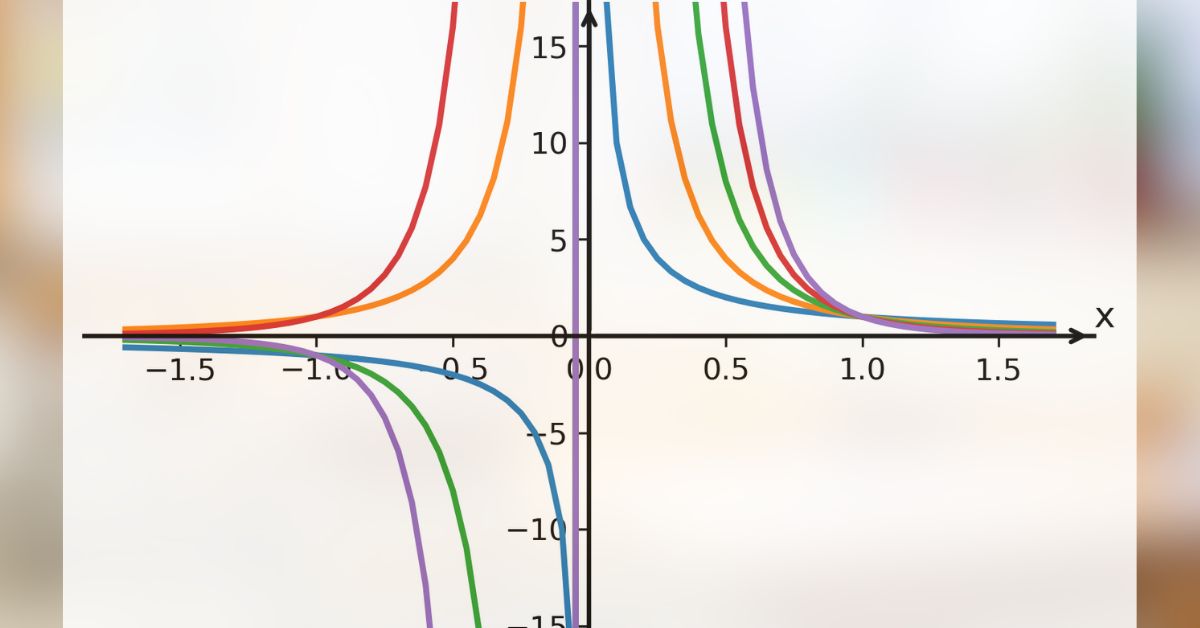
Ukažme si na závěr grafy prvních pěti mocninných funkcí se záporným celým exponentem v jednom obrázku pro jejich lepší srovnání:

Závěr
V tomto článku jsme si probrali mocninné funkce s nulovým a záporným celým exponentem. Navázali jsme tak na předchozí článek, ve kterém jsme se věnovali mocninným funkcím s přirozeným exponentem.
V následujícím článku na chvíli opustíme různé druhy funkcí a podíváme se na pojem inverzní funkce.