Lineární funkce

V předchozím článku jsme se důkladně seznámili s vlastnostmi funkcí. Naše série článků teď bude pokračovat jednotlivými druhy funkcí, které se na středních školách obvykle učí.

Většinou se jedná o tzv. elementární funkce, na které se lze dívat jako na „základní stavební kameny“, z nichž je možné tvořit složitější funkce, ale elementární funkce mají význam i sami o sobě.

Každá elementární funkce má obecný předpis, který když funkce splňuje, pak o ní můžeme říct, že se jedná právě o určitou funkci příslušného druhu. V každém článku si popíšeme právě jednu elementární funkci a zároveň si uvedeme i její vlastnosti.

Hned první a nejjednodušší z elementárních funkcí je lineární funkce.

Obecný předpis lineární funkce

Lineární funkce je každá funkce, která splňuje následující obecný předpis:

$$ f(x): y = ax + b $$

kde a a b jsou konkrétní reálná čísla (konstanty), kterým někdy říkáme koeficienty. Jakmile je zvolíme, definujeme konkrétní lineární funkci. Například pokud zvolíme a = 3 a b = -2, získáme následující lineární funkci:

$$ f(x): y = 3x \; – \; 2 $$ To znamená, že hodnotu y pro libovolné číslo x vypočítáme tak, že toto x vynásobíme číslem 3 a potom od výsledku odečteme číslo 2.

Graf lineární funkce

Grafem lineární funkce je přímka.

Protože přímka je definována dvěma různými body, skrze které prochází, pro sestrojení grafu lineární funkce stačí, když si zvolíme dvě různá čísla x a vypočítáme k nim příslušná čísla y. Dále pomocí takto získaných dvojic nakreslíme do souřadného systému dva body o těchto souřadnicích, které spojíme, a vzniklou úsečku protáhneme v přímku.

Zvolme si např. čísla x₁ = -2 a x₂ = 2 a vypočítejme si příslušné hodnoty y₁ a y₂:

$$ y_1 = 3 \cdot (-2) \; – \; 2 = -8 $$

$$ y_2 = 3 \cdot 2 \; – \; 2 = 4 $$

Takže jsme získaly dvě dvojice čísel: pro x₁ = -2 nám vyšlo y₁ = -8 a pro x₂ = 2 nám vyšlo y₂ = 4.

Výsledky si můžeme zapsat do jednoduché tabulky:

x	-2	2
y	-8	4

Nakreslíme si souřadicový systém, vyneseme do něj body o souřadnicích danými jednotlivými sloupci tabulky [-2; -8] a [2; 4], kterými proložíme přímku, a dostaneme graf naší lineární funkce:

Vlastnosti lineární funkce

Pokud vám nebude význam nějaké vlastnosti jasný, můžete se vrátit k článku Vlastnosti funkcí.

Jestliže v dalším textu nebude řečeno jinak, budeme u popisu vlastností funkce předpokládat, že jsme si její definiční obor neomezili sami.

Pokud je koeficient a kladný (tzn. a > 0), lineární funkce bude rostoucí. To je i náš příklad funkce uvedené výše, kde a = 3.

Pokud je koeficient a záporný (tzn. a < 0), lineární funkce bude klesající. Příkladem klesající lineární funkce může být např. následující funkce g(x):

$$ g(x): y = -\frac{1}{2}x + 1 $$

Sestrojme si opět její graf. Zvolme si dvě čísla x, např. x₁ = -2 a x₂ = 4 a vypočítejme si k nim příslušné hodnoty y₁ a y₂:

$$ y_1 = -\frac{1}{2} \cdot(-2) + 1 = 2 $$

$$ y_2 = -\frac{1}{2} \cdot 4 + 1 = -1 $$

Výsledky si zapíšeme do tabulky:

x	-2	4
y	2	-1

Do souřadnicového systému opět vyneseme body o souřadnicích danými jednotlivými sloupci tabulky [-2; 2] a [4; -1], kterými proložíme přímku:

Definiční obor obou našich funkcí – tedy f(x) i g(x) – tvoří všechna reálná čísla. Oborem hodnot obou funkcí jsou rovněž všechna reálná čísla.

Definiční obor každé lineární funkce tvoří množina všech reálných čísel. Pokud je lineární funkce navíc rostoucí nebo klesající (tuto podmínku splňují všechny lineární funkce až na jednu výjimku, o které si řekneme později), jejím oborem hodnot je rovněž množina všech reálných čísel.

Tedy:

$$ D(f) = R $$

$$ H(f) = R $$

Pokud lineární funkce není konstantní (viz dále), není omezená ani zdola ani shora a nemá v žádném bodě ani mininum ani maximum.

Speciální případy lineární funkce

Existují dva speciální případy lineární funkce, které nastávají tehdy, je-li některý z koeficientů a nebo b nulový.

1. Přímá úměrnost

Přímá úměrnost je speciální případ lineární funkce, kdy koeficient b = 0. Obecný předpis přímé úměrnosti tím pádem můžeme zkrátit takto:

$$ f(x): y = ax + b \rightarrow f(x): y = ax + 0 \rightarrow f(x): y = ax $$

Graf přímé úměrnosti prochází počátkem souřadného systému (bodem [0; 0]). Příkladem může být funkce:

$$ f(x): y = 5x $$

jejíž graf vypadá následovně:

Přímá úměrnost je funkce lichá. (Její graf je středově souměrný podle počátku souřadného systému).

S přímou úměrností se setkáme všude kolem nás. Platí pro ni, že kolikrát zvětšíme hodnotu x, tolikrát se zvětší i hodnota y, a obráceně: kolikrát zmenšíme hodnotu x, tolikrát se zmenší i hodnota y.

Typickým příkladem přímé úměrnosti je závislost částky, kterou zaplatíme za určité zboží, na jeho zakoupeném množství.

Může jít o náš příklad z minulých článků s benzínkou. Pokud cena benzínu bude např. 35,50 Kč za jeden litr, pak můžeme funkci určující závislost částky, kterou za benzín zaplatíme, na jeho zakoupeném množství, vyjádřit následujícím předpisem:

$$ f(x): y = 35{,}50x $$

kde x je množství natankovaného benzínu v litrech a y zaplacená částka v korunách.

U této funkce ale musíme omezit její definiční obor, protože si nemůžeme koupit záporné množství benzínu, takže záporná čísla z něj odstraníme.

Definiční obor pak bude vypadat následovně:

$$ D(f) = \langle 0; +\infty) $$

A vlastní graf takto:

S tím, jak jsme omezili definiční obor této funkce, se změnily i její další vlastnosti:

• Obor hodnot je též omezený na nezáporná čísla.
• Funkce je zdola omezená, protože existuje nejmenší číslo (0), pod které hodnota y nikdy neklesne.
• Funkce má v bodě x = 0 minimum, v žádném bodě nemá maximum.
• Funkce už není lichá (a není ani sudá).

2. Konstantní funkce

Konstantní funkce je speciální případ lineární funkce, kdy se koeficient a = 0. Obecný předpis přímé úměrnosti tím pádem můžeme zkrátit takto:

$$ f(x): y = ax + b \rightarrow f(x): y = 0x + b \rightarrow f(x): y = b $$

Jak vidíme, z předpisu nám úplně vypadla proměnná x a tím pádem na ní hodnota y není vůbec závislá!

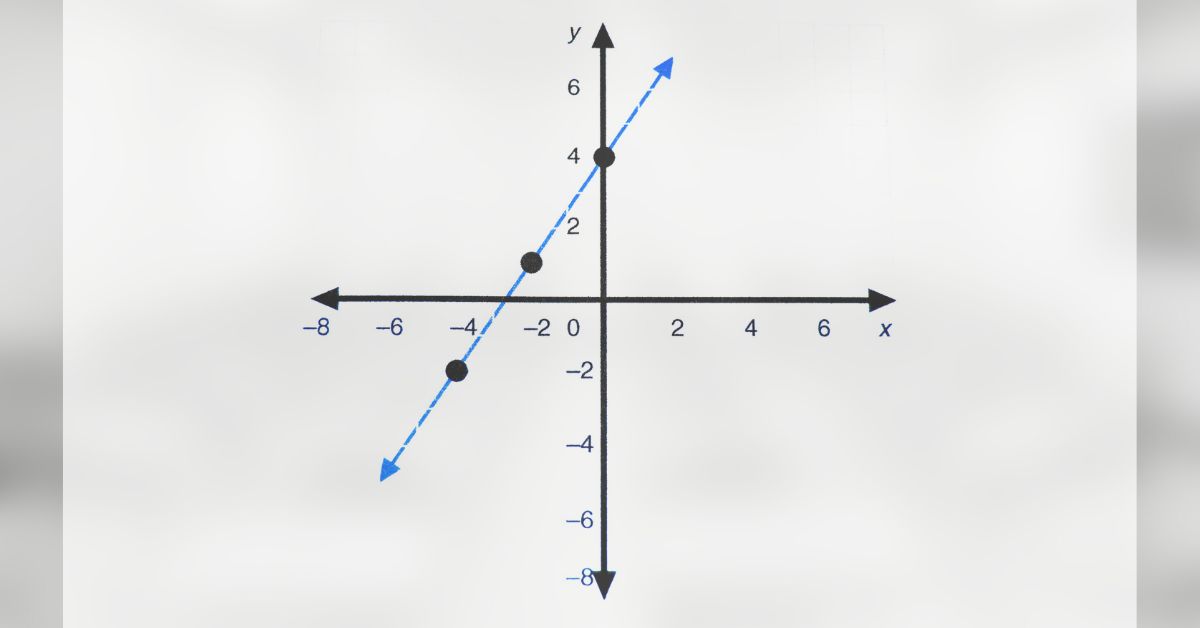
Příkladem konstantní funkce může být např.:

$$ f(x): y = 4 $$

jejíž graf vypadá takto:

Grafem konstantní funkce je vždy přímka rovnoběžná s osou x souřadného systému.

Definičním oborem konstantní funkce jsou stále všechna reálná čísla, což můžeme vyjádřit následujícím zápisem:

$$ D(f) = R $$

Ale obor hodnot konstantní funkce tvoří jediné číslo, a sice hodnota koeficientu b, což je v našem případě 4. Hodnoty y naší konstantní funkce zkrátka nikdy neklesnou pod číslo 4, ani nad něj nevzrostou, protože se stále „drží“ právě na hodnotě 4. Obor hodnot zapíšeme takto:

$$ H(f) = \{4\} $$

Číslo 4 v zápisu oboru hodnot jsme museli dát do množinových (složených) závorek, protože jak definiční obor, tak obor hodnot jsou z matematického hlediska množiny, takže v zápisu celkově pracujeme s množinovou symbolikou. A pokud množinu definujeme výčtem jednotlivých čísel, musíme tato čísla vložit právě do složených závorek, a to i v případě, kdy množina obsahuje pouze jediné číslo.

Konstantní funkce je funkce sudá. (Její graf je osově souměrný podle osy y). Není ani rostoucí, ani klesající, právě proto, že je konstantní, a je omezená.

Závěr

Lineární funkce je možná nejjednodušší funkce vůbec. Ale to neznamená, že by ostatní funkce byly nějak extra složitější.

Jak se s nimi budeme seznamovat v dalších článcích, uvidíte, že se tam stále budou opakovat obecné definice, koeficienty, kreslení grafů a různé vlastnosti, které jste se možná už trochu naučili poznávat právě na základě grafů. A všechny tyto praktiky už jste si „osahali“ v tomto a minulých článcích.

V následujícím článku se podíváme na kvadratickou funkci.