Pojem funkce lze definovat několika způsoby. My si zde uvedeme dva, které se nejčastěji používají ve středoškolské matematice.
Veškeré funkce v této kategorii článků se budou týkat funkcí jedné proměnné, kterou zpravidla značíme x.
1. pojetí – veličinové
Toto pojetí říká, že funkce je pravidlo vyjadřující jednoznačnou závislost proměnné veličiny y na hodnotách nezávisle proměnné veličiny x.
Pojďme si to trochu rozebrat a uvést nějaké příklady.
Co znamená závislost jedné veličiny na druhé? A proč veličinu x nazýváme nezávisle proměnnou a y závisle proměnnou?
Příklad – padající kámen
Dejme tomu, že budeme pouštět kámen z různých výšek (například pater nějaké výškové budovy) a měřit, za jak dlouho dopadne na zem.
Dobu padajícího tělesa z určité výšky spočítáme pomocí následujícího vzorce:
$$ t = \sqrt{\frac{2h}{g}} $$
kde t je doba pádu, h je výška, ze které těleso padá a g tíhové zrychlení na povrchu Země, které má v našich zeměpisných šířkách hodnotu zhruba 9,81 ms-2. Můžeme tedy brát toto číslo jako konstantu a dosadit ji do našeho vzorce, který poté bude vypadat takto:
$$ t = \sqrt{\frac{2h}{9{,}81}} $$
Nyní výšku, ze které těleso padá, místo h označíme písmenem x a dobu volného pádu místo t označíme písmenem y, takže náš vzorec bude mít následující podobu:
$$ y = \sqrt{\frac{2x}{9{,}81}} $$
A získali jsme náš první předpis funkce!
Ve skutečnosti bychom tuto záměnu označení veličin na x a y provádět nemuseli a náš předpis by se stále dal považovat za funkci, ale pokud ji provedeme, bude ihned jasné, která veličina je nezávisle proměnná, a která závisle proměnná.
Pojem proměnná pak znamená, že obě veličiny mohou nabývat různých (proměnných) hodnot.
Veličinu x, která nyní označuje výšku, ze které pouštíme kámen, nazýváme nezávisle proměnnou proto, že může být teoreticky libovolná a volíme si ji my sami. My sami se rozhodujeme, zda budeme kámen pouštět z výšky 10 metrů nebo třeba 50 metrů.
Dosazením do předpisu naší funkce si můžete ověřit, že v případě výšky 10 metrů bude tato doba asi 1,43 sekundy, zatímco v případě 50 metrů to bude zhruba 3,19 sekundy.
Veličina y, která nyní udává dobu volného pádu, je závisle proměnná proto, že její hodnotu si už my sami nevolíme, ale je dána nějakým pravidlem (v tomto případě fyzikálním zákonem). Závisí právě na tom, jakou jsme si zvolili pro volný pád výšku.
V souladu s definicí na začátku této části článku je tedy naše funkce matematické pravidlo vyjadřující jednoznačnou závislost doby volného pádu na hodnotách nezávisle proměnné veličiny, kterou je výška, ze které náš kámen padá.
Příklad – benzínka
Nyní si představme, že jsme v situaci zákazníka, který si přijel na čerpací stanici doplnit benzín, a chceme dopředu vědět, jakou částku zaplatíme za dané množství natankovaného paliva.
Nezávisle proměnná veličina x je v tomto případě množství benzínu, který si hodláme koupit. To si totiž opět volíme sami.
Závisle proměnná veličina y je pak cena, kterou za toto množství zaplatíme. Tu už si sami nevolíme, protože je závislá právě od toho, kolik benzínu natankujeme, a je opět dána nějakým pravidlem, které ji jednoznačně určuje – v tomto případě cenou benzínu za jeden litr.
Bude-li tato cena za litr činit např. 35,50 Kč, pak částka, kterou zaplatíme, bude tvořena součinem tohoto čísla a objemu natankovaného benzínu.
Můžeme tedy definovat funkci udávající závislost celkové ceny natankovaného benzínu na jeho množství:
$$ y = 35{,}5 \cdot x $$
2. pojetí – množinové
Tento přístup pojímá funkci jako jednoznačné přiřazení, které každému prvku x z množiny X přiřazuje právě jeden prvek y z množiny Y. Toto přiřazení se nazývá zobrazení množiny X do množiny Y. Nemusí se jednat o nějaké jiné druhy funkcí než ty, které jsme si popsali ve veličinovém pojetí, jde jen o trochu jiný přístup.
Ve výše uvedeném příkladě s padajícím kamenem bychom mohli říci, že daná funkce je jednoznačné přiřazení, které každému číslu x z množiny X, jež reprezentuje všechny možné výšky, přiřazuje právě jedno číslo y z množiny Y, která představuje všechny možné doby volného pádu.
V množivovém pojetí již tedy nepoužíváme termíny „závisle proměnná“ a „nezávisle proměnná“, protože se na všechno díváme jako na prvky množin.
Příklady množinově pojatých funkcí
Množinové přiřazení nám však umožňuje definovat funkci i jinak než matematickým předpisem – například tabulkou. Představme si funkci, která určuje školní známku na základě toho, na kolik procent (minimálně) student zvládl určitou zkoušku. Taková tabulka by mohla vypadat např. takto:
| x | y |
| 85 | 1 |
| 70 | 2 |
| 55 | 3 |
| 35 | 4 |
| 0 | 5 |
Podobné tabulky pro vybrané hodnoty x a y se dělají běžně při sestrojování grafů funkce, čemuž se budeme věnovat v dalších článcích o funkcích, ale v tomto případě tabulka definuje funkci jako celek. To znamená, že za x můžeme dosadit pouze některé z pěti uvedených čísel (85, 70, 55, 40, 0) a žádné jiné, a všechna možná y tvoří také jen pět čísel (1, 2, 3, 4, 5).
Zkrátka zde nejsou žádné „mezihodnoty“ – např. nic mezi jedničkou a dvojkou, dvojkou a trojkou atd. v případě známky ani nic mezi čísly 85 a 70, 70 a 55 atd. v případě minimálního procentuálního hodnocení.
Dokonce v tomto případě ani neexistuje matematický předpis, který by funkci vyjadřoval – je definována pouze tabulkou. Bylo by sice možné ho sestavit, ale bylo by to poněkud krkolomné, protože hodnoty minimálních procentuálních hodnocení zde nejsou rovnoměrně rozvrženy.
Další příklady
V množinovém pojetí funkce ani nemusíme vždy pracovat s čísly, protože prvky množin mohou být libovolné objekty.
Příklady funkcí v množinovém pojetí:
- X je množina všech automobilů České republiky a Y množina všech státních poznávacích značek. Každý z automobilů x ∈ X má přiřazenou určitou (právě jednu) státní poznávací značku y ∈ Y.
- X je množina všech obyvatel určitého města a Y je množina všech adres tohoto města. Každému obyvateli x ∈ X je přiřazena (právě jedna) adresa y ∈ Y, na níž bydlí.
- X je množina všech platících diváků určitého sportovního utkání a Y je množina všech vstupenek na toto utkání. Každý divák x ∈ X má přiřazenu právě jednu vstupenku y ∈ Y.
Značení funkcí
Každou funkci si můžeme nějak pojmenovat. Funkce se pojmenovávají malými písmeny a máme-li v určitém příkladu jednu funkci, zpravidla ji označíme písmenem f. Máme-li v příkladu více funkcí, používáme následující písmena abecedy jako g, h, i…, nebo jednotlivé funkce můžeme rozlišit číslem v dolním indexu u písmene f, např. f1, f2, f3 atd.
Pokud chceme napsat předpis funkce včetně jejího jména, bude to vypadat nějak takto:
$$ f(x): \; y = \sqrt{\frac{2x}{9,81}} $$
To je nejúplnější zápis předpisu funkce. Písmenem x v závorce u názvu funkce dáváme najevo, že funkce pracuje coby s nezávisle proměnnou právě s hodnotami x.
Často se setkáte se stručnějším zápisem, kdy se uvede pouze název funkce bez označení nezávisle proměnné:
$$ f: \; y = \sqrt{\frac{2x}{9,81}} $$
Jindy se název funkce neuvádí vůbec a napíše se pouze její předpis:
$$ y = \sqrt{\frac{2x}{9,81}} $$
Poměrně vzácně se můžete setkat se zápisem, který obsahuje zase jen název funkce včetně názvu nezávisle proměnné v závorce, za kterým rovnou následuje znak ‚=‘ a pravá strana předpisu funkce (tzn. že se vynechá „y =“):
$$ f(x) = \sqrt{\frac{2x}{9,81}} $$
Když máme takto definovanou funkci (jako f(x) = …), můžeme pak napsat:
$$ y = f(x) $$
Zde za y = … v tomto případě nenásleduje předpis funkce, protože ten už jsme si definovali předtím, a nyní se na něj jen odvoláváme právě jako na f(x).
Může to vypadat poněkud zmateně, ale nejdůležitější je nakonec právě pravá strana zápisu funkce, která definuje ono matematické pravidlo, jež ji definuje. Uvádím zde tyto příklady, protože na různé zápisy předpisů funkcí často narazíte, tak aby vás to nemátlo.
Závěr
Nakonec bych zde rád ukázal jeden obrázek, který jednoduchým způsobem ilustruje, co je to funkce:
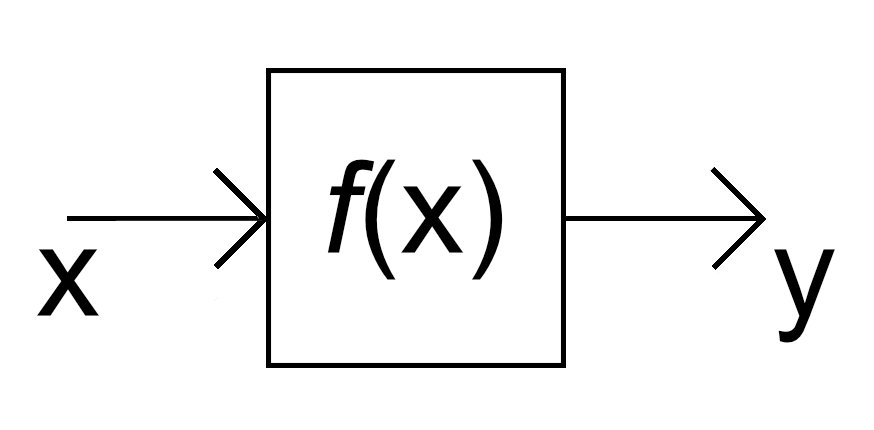
Funkci si můžeme představit prostě jako nějakou „černou skříňku“, jež na vstupu přijme číslo x, které nějakým způsobem zpracuje, a na výstupu vyhodí podle nějakého svého vnitřního předpisu příslušné vypočtené číslo y. V případě množin by x byl prvek nějaké množiny, kterému funkce jednoznačně přiřadí prvek y z jiné množiny.
To je ve zkratce celý její princip. Když si vše výše napsané takto spojíte, zjistíte, že pojem funkce je v podstatě jednoduchý. To by bylo k nejdůležitějším poznatkům ohledně definice funkce vše. Pokud vám není z tohoto článku všechno úplně jasné, vůbec to nevadí, protože pojem funkce pochopíte postupně i z následujích článků, kde se budeme věnovat jejich vlastnostem i konkrtétním druhům. V následujícím článku si ukážeme, co je to graf funkce a definiční obor funkce.


